Правильный восьмиугольник

Выпуклый пятиугольник

Выпуклым пятиугольником называется пятиугольник, такой, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Сумма внутренних углов выпуклого пятиугольника равна 540°.

∑i=15αi=(5−2)⋅180∘=3⋅180∘=540∘{\displaystyle \sum _{i=1}^{5}\alpha _{i}=(5-2)\cdot 180^{\circ }=3\cdot 180^{\circ }=540^{\circ }}

Любые 9 точек в общем положении содержат вершины выпуклого пятиугольника, и существует множество из 8 точек в общем положении, в котором нет выпуклого пятиугольника.
Доказано также, что любые 10 точек на плоскости в общем положении содержат выпуклый пустой пятиугольник, и существует множество из 9 точек в общем положении, в котором нет выпуклого пустого пятиугольника.

Правильный пятиугольник (пентагон)

Свойства диагоналей правильных многоугольников

• Максимальное количество диагоналей правильного n{\displaystyle n}-угольника, пересекающихся в одной точке, не являющейся его вершиной, равно:
  • 2{\displaystyle 2}, если n{\displaystyle n} нечётно;
  • 3{\displaystyle 3}, если n{\displaystyle n} чётно, но не делится на 6{\displaystyle 6};
  • 5{\displaystyle 5}, если n{\displaystyle n} делится на 6{\displaystyle 6}, но не делится на 30{\displaystyle 30};
  • 5{\displaystyle 5}, если n{\displaystyle n} делится на 30{\displaystyle 30}.

Введём функцию δm(n){\displaystyle \delta _{m}(n)}, равную 1{\displaystyle 1} в случае, если n{\displaystyle n} делится на m{\displaystyle m}, и равную {\displaystyle 0} в противном случае. Тогда:

Количество точек пересечения диагоналей правильного n{\displaystyle n}-угольника равно Cn4+(−5n3+45n2−70n+24)/24⋅δ2(n)−(3n/2)⋅δ4(n)++(−45n2+262n)/6⋅δ6(n)+42n⋅δ12(n)+60n⋅δ18(n)++35n⋅δ24(n)−38n⋅δ30(n)−82n⋅δ42(n)−330n⋅δ60(n)−−144n⋅δ84(n)−96n⋅δ90(n)−144n⋅δ120(n)−96n⋅δ210(n){\displaystyle {\begin{array}{l}C_{n}^{4}+\left(-5n^{3}+45n^{2}-70n+24\right)/24\cdot \delta _{2}(n)-(3n/2)\cdot \delta _{4}(n)+\\+\left(-45n^{2}+262n\right)/6\cdot \delta _{6}(n)+42n\cdot \delta _{12}(n)+60n\cdot \delta _{18}(n)+\\+35n\cdot \delta _{24}(n)-38n\cdot \delta _{30}(n)-82n\cdot \delta _{42}(n)-330n\cdot \delta _{60}(n)-\\-144n\cdot \delta _{84}(n)-96n\cdot \delta _{90}(n)-144n\cdot \delta _{120}(n)-96n\cdot \delta _{210}(n)\end{array}}}

Где Cn4{\displaystyle C_{n}^{4}} — число сочетаний из n{\displaystyle n} по 4{\displaystyle 4}.

Количество частей, на которые правильный n{\displaystyle n}-угольник делят его диагонали, равно (n4−6n3+23n2−42n+24)/24++(−5n3+42n2−40n−48)/48⋅δ2(n)−(3n/4)⋅δ4(n)++(−53n2+310n)/12⋅δ6(n)+(49n/2)⋅δ12(n)+32n⋅δ18(n)++19n⋅δ24(n)−36n⋅δ30(n)−50n⋅δ42(n)−190n⋅δ60(n)−−78n⋅δ84(n)−48n⋅δ90(n)−78n⋅δ120(n)−48n⋅δ210(n){\displaystyle {\begin{array}{l}\left(n^{4}-6n^{3}+23n^{2}-42n+24\right)/24+\\+\left(-5n^{3}+42n^{2}-40n-48\right)/48\cdot \delta _{2}(n)-(3n/4)\cdot \delta _{4}(n)+\\+\left(-53n^{2}+310n\right)/12\cdot \delta _{6}(n)+(49n/2)\cdot \delta _{12}(n)+32n\cdot \delta _{18}(n)+\\+19n\cdot \delta _{24}(n)-36n\cdot \delta _{30}(n)-50n\cdot \delta _{42}(n)-190n\cdot \delta _{60}(n)-\\-78n\cdot \delta _{84}(n)-48n\cdot \delta _{90}(n)-78n\cdot \delta _{120}(n)-48n\cdot \delta _{210}(n)\end{array}}}

.

Варианты определений

Существуют три различных варианта определения многоугольника; последнее определение является наиболее распространённым.

• Плоская замкнутая ломаная — наиболее общий случай;
• Плоская замкнутая ломаная без самопересечений, любые два соседних звена которой не лежат на одной прямой;
• Часть плоскости, ограниченная замкнутой ломаной без самопересечений — плоский многоугольник; в этом случае сама ломаная называется контуром многоугольника.

Существуют также несколько вариантов обобщения данного определения, допускающие бесконечное число звеньев ломаных, несколько несвязных граничных ломаных, ломаные в пространстве, произвольные отрезки непрерывных кривых вместо отрезков прямых и др.

Другие восемнадцатиугольники фигуры

Звёздчатые 18{\displaystyle 18}-угольники имеют символы {18n}{\displaystyle \{18/n\}}. Существует два правильных звёздчатых многоугольника: 185{\displaystyle {18/5}} и {187}{\displaystyle \{18/7\}}. Они используют те же самые вершины, но соединяют каждую пятую или седьмую вершину. Имеются также составные восемнадцатиугольники: {182}{\displaystyle \{18/2\}} эквивалентен 2{9}{\displaystyle 2\{9\}} (двум девятиугольникам), {183}{\displaystyle \{18/3\}} эквивалентен 3{6}{\displaystyle 3\{6\}} (трём шестиугольникам), {184}{\displaystyle \{18/4\}} и {188}{\displaystyle \{18/8\}} эквивалентны 2{92}{\displaystyle 2\{9/2\}} и 2{94}{\displaystyle 2\{9/4\}} (двум эннеаграммам), {186}{\displaystyle \{18/6\}} эквивалентен 6{3}{\displaystyle 6\{3\}} (6{\displaystyle 6} равносторонним треугольникам), и, наконец, {189}{\displaystyle \{18/9\}} эквивалентен 9{2}{\displaystyle 9\{2\}} (девять двуугольников).

Составные и звёздчатые многоугольники
n	1	2	3	4	5	6	7	8	9
Вид	Выпуклый многоугольник	Составные	Звёздчатый многоугольник	Составной	Звёздчатый многоугольник	Составной
Рисунок	{181}{\displaystyle \{18/1\}} = {18}{\displaystyle \{18\}}	{182}{\displaystyle \{18/2\}} = 2{9}{\displaystyle 2\{9\}}	{183}{\displaystyle \{18/3\}} = 3{6}{\displaystyle 3\{6\}}	{184}{\displaystyle \{18/4\}} = 2{92}{\displaystyle 2\{9/2\}}	{185}{\displaystyle \{18/5\}}	{186}{\displaystyle \{18/6\}} = 6{3}{\displaystyle 6\{3\}}	{187}{\displaystyle \{18/7\}}	{188}{\displaystyle \{18/8\}} = 2{94}{\displaystyle 2\{9/4\}}	{189}{\displaystyle \{18/9\}} = 9{2}{\displaystyle 9\{2\}}
Внутренний угол	160∘{\displaystyle 160^{\circ }}	140∘{\displaystyle 140^{\circ }}	120∘{\displaystyle 120^{\circ }}	100∘{\displaystyle 100^{\circ }}	80∘{\displaystyle 80^{\circ }}	60∘{\displaystyle 60^{\circ }}	40∘{\displaystyle 40^{\circ }}	20∘{\displaystyle 20^{\circ }}	∘{\displaystyle 0^{\circ }}

Более глубокие усечения правильного многоугольника и правильной эннеаграммы дают равноугольные (вершинно-транзитивные) промежуточные восемнадцатиугольники с находящимися на равном расстоянии вершинами и двумя длинами сторон. Другие усечения дают двойное покрытие: t{98}={188}=2{94},t{94}={184}=2{92},t{92}={182}=2{9}{\displaystyle \mathrm {t} \{9/8\}=\{18/8\}=2\{9/4\},\;\mathrm {t} \{9/4\}=\{18/4\}=2\{9/2\},\;\mathrm {t} \{9/2\}=\{18/2\}=2\{9\}}.

Вершинно-транзитивные усечения девятиугольника и эннеаграмм
Квазиправильные	Изогональные	КвазиправильныеДвойное покрытие
t9=18{\displaystyle \mathrm {t} {9}={18}}					t98=188{\displaystyle \mathrm {t} {9/8}={18/8}}=294{\displaystyle =2{9/4}}
t95=185{\displaystyle \mathrm {t} {9/5}={18/5}}					t94=184{\displaystyle \mathrm {t} {9/4}={18/4}}=292{\displaystyle =2{9/2}}
t97=187{\displaystyle \mathrm {t} {9/7}={18/7}}					t92=182{\displaystyle \mathrm {t} {9/2}={18/2}}=29{\displaystyle =2{9}}

Многоугольники Петри

Правильный восемнадцатиугольник является многоугольником Петри для ряда политопов, что показано в косоортогональных проекциях на :

Восемнадцатиугольные многоугольники Петри
A17	B9	D10	E7
17-симплекс		Эннеракт					>

Звездчатые пятиугольники

Золотые сечения пентаграммы

Основная статья: Пентаграмма

Многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника называется звёздчатым. Помимо правильного существует ещё один звёздчатый пятиугольник — пентаграмма.

Пентаграмма, как полагал Пифагор, представляет собой математическое совершенство, поскольку демонстрирует золотое сечение (φ = (1+√5)/2 = 1,618…). Если разделить длину любого цветного отрезка на длину самого длинного из оставшихся меньших отрезков, то будет получено золотое сечение φ.

φ=redblue=bluegreen=greenmagenta{\displaystyle \varphi ={\frac {\mathrm {\color {red}red} }{\mathrm {\color {Blue}blue} }}={\frac {\mathrm {\color {Blue}blue} }{\mathrm {\color {Green}green} }}={\frac {\mathrm {\color {Green}green} }{\mathrm {\color {Magenta}magenta} }}}

От теории к практике

Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.

Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:

Выпускается и бетонная плитка для мощения.

https://youtube.com/watch?v=dXAWHtYgFyQ

Определение и построение

Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.

Если вспомнить формулу суммы углов многоугольника

180°(n-2),

то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.

Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.

Пошаговая инструкция будет выглядеть так:

1. чертится прямая линия и на ней ставится точка;
2. из этой точки строится окружность (она является ее центром);
3. из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
4. после этого отрезками последовательно соединяются все точки на первой окружности.

При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.

Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.

Симметрия

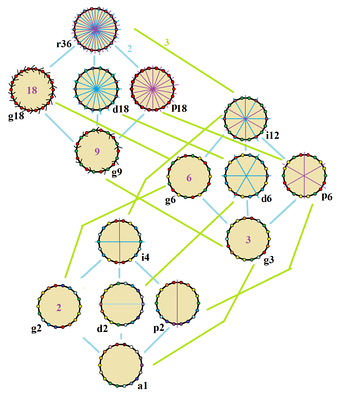
Группы симметрии правильного восемнадцатиугольника. Симметричные вершины окрашены в одинаковые цвета. Голубые зеркала проведены через вершины, фиолетовые — через стороны. Порядки групп вращений даны в центре.

Правильный восемнадцатиугольник имеет диэдральную группу D18{\displaystyle \mathrm {D} _{18}} порядка 36{\displaystyle 36}. Имеется 5{\displaystyle 5} типов подгрупп диэдральной симметрии: D9{\displaystyle \mathrm {D} _{9}}, (D6{\displaystyle \mathrm {D} _{6}}, D3{\displaystyle \mathrm {D} _{3}}) и (D2{\displaystyle \mathrm {D} _{2}}, D1{\displaystyle \mathrm {D} _{1}}), а также 6 циклических групп симметрии: (Z18{\displaystyle \mathrm {Z} _{18}}, Z9{\displaystyle \mathrm {Z} _{9}}), (Z6{\displaystyle \mathrm {Z} _{6}}, Z3{\displaystyle \mathrm {Z} _{3}}) и (Z2{\displaystyle \mathrm {Z} _{2}}, Z1{\displaystyle \mathrm {Z} _{1}}).

На рисунке справа можно видеть 15{\displaystyle 15} подгрупп симметрии восемнадцатиугольника. Конвей использовал для их обозначения буквы вместе с порядком группы. Полная симметрия правильной фигуры будет равна r36{\displaystyle \mathrm {r} 36}, а отсутствие симметрии (то есть тривиальная группа) отмечается как a1{\displaystyle \mathrm {a} 1}. Диэдральные симметрии делятся по тому, проходят ли их оси через вершины (используется буква d{\displaystyle \mathrm {d} }, от «diagonal») или через середины сторон (используется буква p{\displaystyle \mathrm {p} }, от «perpendicular»). Если же оси симметрии проходят и через вершины, и через середины сторон, используется буква i{\displaystyle \mathrm {i} }. Циклические группы отмечаются буквой g{\displaystyle \mathrm {g} } (от «gyration»).

Все эти подгруппы могут являться диэдральными группами неправильных восемнадцатиугольников, и лишь подгруппа g18{\displaystyle \mathrm {g} 18} не даёт свободы в этом отношении, если только стороны многоугольника не рассматриваются как имеющие направление, то есть как векторы.

Правильный восемнадцатиугольник

Правильный восемнадцатиугольник имеет символ Шлефли {18}{\displaystyle \{18\}} и может быть построен как полуправильный усечённый девятиугольник, t{9}{\displaystyle \mathrm {t} \{9\}}, в котором перемежаются два типа сторон.

Построение

Имея 18=2⋅32{\displaystyle 18=2\cdot 3^{2}} сторон, правильный восемнадцатиугольник не может быть построен с помощью циркуля и линейки по теореме Гаусса — Ванцеля. Однако его можно построить с помощью невсиса или трисекции угла с использованием томагавка.

Точное построение восемнадцатиугольника, основанное на трисекции угла 120° с помощью томагавка. Анимация длится 1м 34с.

Следующее приближённое построение очень близко к построению девятиугольника, поскольку восемнадцатиугольник, как уже было сказано выше, может быть построен путём усечения девятиугольника. Данное построение возможно сделать с помощью только циркуля и линейки.

Построение

Углы сглаженного восьмиугольника можно найти путём вращения трёх правильных восьмиугольников, центры которых образуют треугольник с постоянной площадью.

При рассмотрении семейств максимально плотных упаковок сглаженного восьмиугольника, требование, что плотность упаковки остаётся неизменной при изменении точки соприкосновения соседних восьмиугольников, может быть использовано для определения формы углов. На рисунке три восьмиугольника вращаются, в то время как площадь треугольника, образованного центрами этих восьмиугольников, не меняется. Для правильных восьмиугольников красные и синие фрагменты перекрываются, так что для возможности вращения необходимо углы срезать в точке, лежащей на полпути между центрами восьмиугольников, что даёт кривую, которая оказывается гиперболой.

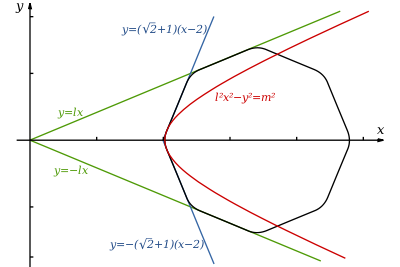
Построение сглаженного восьмиугольника (чёрная линия), касательная гипербола (красная линия) и асимптоты этой гиперболы (зелёные линии) и касательные стороны к гиперболе (синие линии).

Гипербола строится как касательная к двум сторонам восьмиугольника и имеющая асимптотами две смежные этим сторонам стороны восьмиугольника. Расположим правильный восьмиугольник с радиусом описанной окружности 2{\displaystyle {\sqrt {2}}} и центром в точке (2+2,){\displaystyle (2+{\sqrt {2}},0)}. Одна вершина будет находиться в точке (2,){\displaystyle (2,0)}. Определим две константы, ℓ и m:

ℓ=2−1{\displaystyle \ell ={\sqrt {2}}-1}

m=124{\displaystyle m={\sqrt{\frac {1}{2}}}}

Гипербола тогда задаётся уравнением

ℓ2×2−y2=m2{\displaystyle \ell ^{2}x^{2}-y^{2}=m^{2}}

или, в эквивалентной параметризованной форме (только для правой части гиперболы):

{x=mℓcosh⁡ty=msinh⁡t−∞<t<∞{\displaystyle {\begin{cases}x={\frac {m}{\ell }}\cosh {t}\\y=m\sinh {t}\end{cases}}-\infty <t<\infty }

Порция гиперболы, которая образует углы, задаётся значениями параметра

−ln⁡24<t<ln⁡24{\displaystyle -{\frac {\ln {2}}{4}}<t<{\frac {\ln {2}}{4}}}

Прямые восьмиугольника, касательные гиперболе

y=±(2+1)(x−2){\displaystyle y=\pm \left({\sqrt {2}}+1\right)\left(x-2\right)}

Асимптоты к гиперболе

y=±ℓx.{\displaystyle y=\pm \ell x.}

Свойства простые и интересные

Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:

Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:

1. диаметр описанной окружности;
2. диаметр вписанной окружности;
3. площадь;
4. периметр.

Описанная окружность и возможность построения

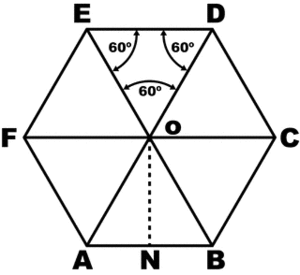
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.

Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.

После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:

R=а.

Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.

Ну а площадь этой окружности будет стандартная:

S=πR²

Вписанная окружность

Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.

Высота равностороннего треугольника вычисляется просто:

h²=а²-(а/2)²= а²3/4, h=а(√3)/2

А поскольку R=a и r=h, то получается, что

r=R(√3)/2.

Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.

Ее площадь будет составлять:

S=3πa²/4,

то есть три четверти от описанной.

Периметр и площадь

С периметром все ясно, это сумма длин сторон:

P=6а, или P=6R

S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или

S=3R²(√3)/2

Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:

S=3(2r/√3)²(√3)/2=r²(2√3)

Занимательные построения

В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:

Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:

1. Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
2. Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
3. Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.

Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:

1. Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
2. Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
3. Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
4. Углы новообразованного шестиугольника равняются 360-120-60-60=120°.

Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:

d=а(√3)/3

Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:

r₂=а/2

Площадь нового шестиугольника можно посчитать так:

S=(3(√3)/2)(а(√3)/3)²=а(√3)/2

Применение восьмиугольников[править | править код]

Дорожный знак «Движение без остановки запрещено»

Восьмиугольный план Купола Скалы

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.

Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и . Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.

Максимальная плотность упаковки

Сглаженный восьмиугольник имеет максимальную плотность упаковки

8−42−ln⁡222−1≈0.902414.{\displaystyle {\frac {8-4{\sqrt {2}}-\ln {2}}{2{\sqrt {2}}-1}}\approx 0.902414\,.}

Эта плотность меньше максимальной плотности упаковки кругов, которая равна

π12≈0.906899.{\displaystyle {\frac {\pi }{\sqrt {12}}}\approx 0.906899.}

Максимальная плотность упаковки обычных правильных восьмиугольников равна

4+425+42≈0.906163,{\displaystyle {\frac {4+4{\sqrt {2}}}{5+4{\sqrt {2}}}}\approx 0.906163,}

что также слегка меньше максимальной плотности упаковки кругов, но больше плотности упаковки сглаженного восьмиугольника.

Сглаженный восьмиугольник достигает максимальной плотности упаковки не только для единственной упаковки, а для однопараметрического семейства упаковок. Все они являются решёточными упаковками.

Для трёхмерного пространства утверждает, что нет выпуклой фигуры, имеющей наибольшую плотность упаковки, меньшую упаковки шаров.

Литература

• Henry Adams. Cassell’s Engineer’s Handbook: Comprising Facts and Formulæ, Principles and Practice, in All Branches of Engineering. — D. McKay, 1907. — С. 528.
• John B. Conway. Mathematical Connections: A Capstone Course. — American Mathematical Society, 2010. — С. 31. — ISBN 9780821849798.
• L. Christine Kinsey, Teresa E. Moore. Symmetry, Shape, and Surfaces: An Introduction to Mathematics Through Geometry. — Springer, 2002. — С. 86. — ISBN 9781930190092.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — Wellesley, MA: A K Peters, Ltd., 2008. — ISBN 978-1-56881-220-5.
• Branko Grünbaum. The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History / Richard K.Guy, Robert E. Woodrow. — The Mathematical Association of America, 1994. — (MAA Spectrum). — ISBN 0-88385-516-X.
• Elmslie William Dallas. The Elements of Plane Practical Geometry, Etc. — John W. Parker & Son, 1855.

Восьмиугольник

Площадь через квадрат

Площадь правильного восьмиугольника можно вычислить как площадь усечённого квадрата.

Площадь можно также вычислить как усечение квадрата

S=A2−a2,{\displaystyle S=A^{2}-a^{2},}

где A — ширина восьмиугольника (вторая меньшая диагональ), а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить (как на рисунке), получится квадрат со стороной a.

Если задана сторона a, то длина A равна

A=a2+a+a2=(1+2)a≈2.414a.{\displaystyle A={\frac {a}{\sqrt {2}}}+a+{\frac {a}{\sqrt {2}}}=(1+{\sqrt {2}})a\approx 2.414a.}

Тогда площадь равна:

S=((1+2)a)2−a2=2(1+2)a2≈4.828a2.{\displaystyle S=((1+{\sqrt {2}})a)^{2}-a^{2}=2(1+{\sqrt {2}})a^{2}\approx 4.828a^{2}.}

Площадь через A (ширину восьмиугольника)

S=2(2−1)A2≈0.828A2.{\displaystyle S=2({\sqrt {2}}-1)A^{2}\approx 0.828A^{2}.}

Ещё одна простая формула площади:

 S=2aA.{\displaystyle \ S=2aA.}

Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем

a≈A2.414.{\displaystyle a\approx A/2.414.}

Два катета углового треугольника можно получить по формуле

e=(A−a)2.{\displaystyle e=(A-a)/2.}