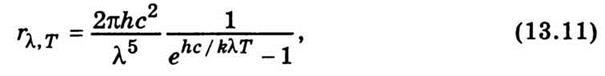Планковские единицы
Содержание:
- Квантование пространства и планковская длина
- Основные единицы
- Производные единицы
- История
- Планковская длина и евклидова геометрия
- Значения других единиц, равные введённым выше
- Метрическая система
- Британские и американские единицы
- Английские инжернерные и британские гравитационные единицы
- Естественнные единицы
- Плотности различных веществ
Квантование пространства и планковская длина
В середине прошлого века гипотеза о квантовании пространства-времени на пути объединения квантовой механики и общей теории относительности привела к предположению о том, что существуют ячейки пространства-времени с минимально возможной длиной, равной фундаментальной длине. Согласно этой гипотезе, степень влияния квантования пространства на проходящий свет зависит от размеров ячейки. Для исследования необходимо интенсивное излучение, прошедшее как можно большее расстояние. В настоящее время группа ученых воспользовалась данными съёмки гамма-вспышки GRB 041219A, осуществленной с европейского космического телескопа Integral. Гамма-вспышка GRB 041219A вошла в 1% самых ярких гамма-вспышек за весь период наблюдения, а расстояние до её источника не менее 300 миллионов световых лет. Наблюдение «Интеграла» позволило оценить размер ячейки на несколько порядков точнее, чем все предыдущие опыты такого плана.
Анализ данных показал — если зернистость пространства вообще существует, то она должна быть на уровне 10−48 метров или меньше. О дискредитации теории квантования пространства и времени говорить еще рано. В запасе есть два варианта объяснения этого факта. Первый вариант исходит из того, что на микроуровне — в планковском масштабе — пространство и время варьируются одновременно друг с другом, так что скорость распространения фотонов при этом не меняется. предполагает, что неоднородности скорости определяются не планковской длиной, а ее квадратом, так что эти неоднородности становятся неизмеримо малыми.
Основные единицы
Ныне под планковской системой понимается система единиц, в которой в качестве основных единиц выбраны следующие фундаментальные физические постоянные:
- ℏ{\displaystyle \hbar } — постоянная Дирака (постоянная Планка, делённая на 2π{\displaystyle 2\pi });
- c{\displaystyle c} — скорость света (электродинамическая постоянная);
- G{\displaystyle G} — гравитационная постоянная;
- k{\displaystyle k} — постоянная Больцмана.
При этом значение коэффициента пропорциональности в законе Кулона выбрано равным единице.
Обычно, говоря о планковской системе, указывают, что в этом случае выполняется c=1,{\displaystyle c=1,} ℏ=1,{\displaystyle \hbar =1,} k=1{\displaystyle k=1} и G=1.{\displaystyle G=1.} Однако в действительности такая форма записи не точна. Она отражает лишь то, что соответствующая постоянная выбрана в качестве меры. Следует иметь в виду, что в планковской системе размерности отнюдь не исчезают, скорее наоборот, они приобретают фундаментальный характер, поскольку составляются из фундаментальных постоянных.
Производные единицы
Из основных планковских единиц выводятся все остальные (производные) единицы системы, часть из которых приведена ниже. Значения c,G,ℏ{\displaystyle c,\,G,\,\hbar } и k{\displaystyle k} в единицах Международной системы единиц (СИ), использованные в расчётах, рекомендованы CODATA.
- Планковская масса mP=ℏcG≈2,176434(24)×10−8{\displaystyle m_{\text{P}}={\sqrt {\frac {\hbar c}{G}}}\approx 2{,}176434(24)\times 10^{-8}} кг.
- Планковская длина lP=ℏmPc=ℏGc3≈1,616255(18)×10−35{\displaystyle l_{\text{P}}={\frac {\hbar }{m_{\text{P}}c}}={\sqrt {\frac {\hbar G}{c^{3}}}}\approx 1{,}616255(18)\times 10^{-35}} м.
- Планковское время tP=lPc=ℏGc5≈5,391247(60)×10−44{\displaystyle t_{\text{P}}={\frac {l_{\text{P}}}{c}}={\sqrt {\frac {\hbar G}{c^{5}}}}\approx 5{,}391247(60)\times 10^{-44}} с.
- Планковское ускорение aP=lPtP2=ctP≈5,561×1051{\displaystyle a_{\text{P}}={\frac {l_{\text{P}}}{t_{\text{P}}^{2}}}={\frac {c}{t_{\text{P}}}}\approx 5{,}561\times 10^{51}} м/с2.
- Планковская энергия EP=mPc2=ℏtP=ℏc5G≈1,9561×109{\displaystyle E_{\text{P}}=m_{\text{P}}c^{2}={\frac {\hbar }{t_{\text{P}}}}={\sqrt {\frac {\hbar c^{5}}{G}}}\approx 1{,}9561\times 10^{9}} Дж.
- Планковская температура TP=EPk=ℏc5k2G≈1,416784(16)×1032{\displaystyle T_{\text{P}}={\frac {E_{\text{P}}}{k}}={\sqrt {\frac {\hbar c^{5}}{k^{2}G}}}\approx 1{,}416784(16)\times 10^{32}} К.
- Планковский заряд qP=4πεℏc=2chε=eα≈1,8755459×10−18{\displaystyle q_{\text{P}}={\sqrt {4\pi \varepsilon _{0}\hbar c}}={\sqrt {2ch\varepsilon _{0}}}={\frac {e}{\sqrt {\alpha }}}\approx 1{,}8755459\times 10^{-18}} Кл, где e{\displaystyle e} — элементарный электрический заряд, α{\displaystyle \alpha } — постоянная тонкой структуры, h{\displaystyle h} — постоянная Планка. Соответственно, постоянная тонкой структуры — это квадрат заряда электрона, выраженного в планковских зарядах.
- Планковский ток IP=qPtP=c64πεG=2c3πεG≈3,4789×1025{\displaystyle I_{\text{P}}=q_{\text{P}}/t_{\text{P}}={\sqrt {c^{6}4\pi \varepsilon _{0}/G}}=2c^{3}{\sqrt {\pi \varepsilon _{0}/G}}\approx 3{,}4789\times 10^{25}} А.
- Планковская сила FP=mPctP=c4G=1,21027×1044{\displaystyle F_{\text{P}}={\frac {m_{\text{P}}c}{t_{\text{P}}}}={\frac {c^{4}}{G}}=1{,}21027\times 10^{44}} Н.
- Планковское давление pP=FPlP2=c7ℏG2≈4,63309×10113{\displaystyle p_{\text{P}}={\frac {F_{\text{P}}}{l_{\text{P}}^{2}}}={\frac {c^{7}}{\hbar G^{2}}}\approx 4,63309\times 10^{113}} Па,
- Планковская угловая частота ωP=1tP=c5ℏG≈1,85487×1043{\displaystyle \omega _{\text{P}}={\frac {1}{t_{\text{P}}}}={\sqrt {\frac {c^{5}}{\hbar G}}}\approx 1{,}85487\times 10^{43}} c−1.
- Планковская мощность (или светимость) LP=mPc2tP=c5G≈3,62831×1052{\displaystyle L_{\mathrm {P} }={\frac {m_{\text{P}}c^{2}}{t_{\text{P}}}}={\frac {c^{5}}{G}}\approx 3{,}62831\times 10^{52}} Вт.
История
Система планковских единиц впервые предложена в 1899 году Максом Планком на основе скорости света c{\displaystyle c}, гравитационной постоянной G{\displaystyle G} и двух ввёденных им новых постоянных теории теплового излучения a{\displaystyle a} и b{\displaystyle b} (они отличаются от современных постоянных hk{\displaystyle {\frac {h}{k}}} и h{\displaystyle h} на безразмерные множители). Первоначально планковские единицы были введены в докладе, сделанном 18 мая 1899 года на заседании Академии наук в Берлине и посвящённом обзору теории явлений теплового излучения, рассматриваемых с точки зрения электромагнитной теории света, и значению второго начала термодинамики в ней.
В 1900 году Макс Планк предложил новый закон излучения (закон Планка), в котором фигурировали две новые постоянные h{\displaystyle h} и k.{\displaystyle k.} В 1901 году Планком была предложена система на основе постоянных c,{\displaystyle c,} G,{\displaystyle G,} h{\displaystyle h} и k{\displaystyle k}.
Планковская длина и евклидова геометрия
Гравитационное поле совершает нулевые колебания, и связанная с ним геометрия тоже колеблется. Отношение длины окружности к радиусу колеблется около евклидова значения: чем меньше масштаб, тем большими становятся отклонения от евклидовой геометрии. Оценим порядок длины волны нулевых гравитационных колебаний, при которой геометрия становится совсем не похожей на евклидову. Степень отклонения ζ{\displaystyle \zeta } геометрии от евклидовой в гравитационном поле определяется отношением гравитационного потенциала φ{\displaystyle \varphi } и квадрата скорости света c{\displaystyle c} : ζ=φc2{\displaystyle \zeta =\varphi /c^{2}}. Когда ζ≪1{\displaystyle \zeta \ll 1}, геометрия близка к евклидовой; при ζ∼1{\displaystyle \zeta \sim 1} всякое сходство исчезает. Энергия колебания масштаба l{\displaystyle l} равна E=ℏν∼ℏcl{\displaystyle E=\hbar \nu \sim \hbar c/l} (cl{\displaystyle c/l} — порядок частоты колебаний). Гравитационный потенциал, создаваемый массой m{\displaystyle m}, на такой длине есть φ=Gml{\displaystyle \varphi =Gm/l}, где G{\displaystyle G} — постоянная всемирного тяготения. Вместо m{\displaystyle m} следует подставить массу, которой, согласно формуле Эйнштейна, соответствует энергия E{\displaystyle E} (m=Ec2{\displaystyle m=E/c^{2}}). Получаем φ=GElc2=Gℏl2c{\displaystyle \varphi =GE/l\,c^{2}=G\hbar /l^{2}c}. Разделив это выражение на c2{\displaystyle c^{2}}, получим величину отклонения ζ=Gℏc3l2=ℓP2l2{\displaystyle \zeta =G\hbar /c^{3}l^{2}=\ell _{P}^{2}/l^{2}}. Приравняв ζ=1{\displaystyle \zeta =1}, найдем ту длину, на которой полностью искажается евклидова геометрия. Она равна планковской длине ℓP=Gℏc3≈10−35{\displaystyle \ell _{P}={\sqrt {G\hbar /c^{3}}}\approx 10^{-35}}м.
Значения других единиц, равные введённым выше
открыть
свернуть
Метрическая система
|
планковская плотность → тонна на кубометр (т/м³) |
|
|
планковская плотность → килограмм на кубометр (кг/м³) |
|
|
планковская плотность → грамм на кубометр (г/м³) |
|
|
планковская плотность → миллиграмм на кубометр (мг/м³) |
|
|
планковская плотность → килограмм на литр (кг/л) |
|
|
планковская плотность → грамм на литр (г/л) |
|
|
планковская плотность → миллиграмм на литр (мг/л) |
|
|
планковская плотность → килограмм на кубический дециметр (кг/дм³) |
|
планковская плотность → грамм на кубический дециметр (г/дм³) |
|
|
планковская плотность → миллиграмм на кубический дециметр (мг/дм³) |
|
|
планковская плотность → килограмм на кубический сантиметр (кг/см³) |
|
|
планковская плотность → грамм на кубический сантиметр (г/см³) |
|
|
планковская плотность → миллиграмм на кубический сантиметр (мг/см³) |
|
|
планковская плотность → килограмм на миллилитр (кг/мл) |
|
|
планковская плотность → грамм на миллилитр (г/мл) |
|
|
планковская плотность → миллиграмм на миллилитр (мг/мл) |
Единицы:
тонна на кубометр
(т/м³)
/
килограмм на кубометр
(кг/м³)
/
грамм на кубометр
(г/м³)
/
миллиграмм на кубометр
(мг/м³)
/
килограмм на литр
(кг/л)
/
грамм на литр
(г/л)
/
миллиграмм на литр
(мг/л)
/
килограмм на кубический дециметр
(кг/дм³)
/
грамм на кубический дециметр
(г/дм³)
/
миллиграмм на кубический дециметр
(мг/дм³)
/
килограмм на кубический сантиметр
(кг/см³)
/
грамм на кубический сантиметр
(г/см³)
/
миллиграмм на кубический сантиметр
(мг/см³)
/
килограмм на миллилитр
(кг/мл)
/
грамм на миллилитр
(г/мл)
/
миллиграмм на миллилитр
(мг/мл)
открыть
свернуть
Британские и американские единицы
|
планковская плотность → фунты на кубический ярд (lb/yd³) |
|
|
планковская плотность → фунты на кубический фут (lb/ft³) |
|
|
планковская плотность → фунты на кубический дюйм (lb/in³) |
|
|
планковская плотность → фунты на галлон США (lb/gal) |
|
| планковская плотность → фунты на британский галлон | |
| планковская плотность → фунты на бушель США |
|
планковская плотность → унции на кубический ярд (oz/yd³) |
|
|
планковская плотность → унции на кубический фунт (oz/ft³) |
|
|
планковская плотность → унции на кубический дюйм (oz/in³) |
|
|
планковская плотность → унции на галлон США (oz/gal) |
|
| планковская плотность → унции на британский галлон | |
| планковская плотность → унции на бушель США |
Единицы:
фунты на кубический ярд
(lb/yd³)
/
фунты на кубический фут
(lb/ft³)
/
фунты на кубический дюйм
(lb/in³)
/
фунты на галлон США
(lb/gal)
/
фунты на британский галлон
/
фунты на бушель США
/
унции на кубический ярд
(oz/yd³)
/
унции на кубический фунт
(oz/ft³)
/
унции на кубический дюйм
(oz/in³)
/
унции на галлон США
(oz/gal)
/
унции на британский галлон
/
унции на бушель США
открыть
свернуть
Английские инжернерные и британские гравитационные единицы
|
планковская плотность → Слаг на кубический ярд (slug/yd³) |
|
планковская плотность → Слаг на кубический фут (slug/ft³) |
|
|
планковская плотность → Слаг на кубический дюйм (slug/in³) |
Единицы:
Слаг на кубический ярд
(slug/yd³)
/
Слаг на кубический фут
(slug/ft³)
/
Слаг на кубический дюйм
(slug/in³)
открыть
свернуть
Естественнные единицы
В физике естественные единицы измерения базируются только на фундаментальных физических константах. Определение этих единиц никак не связано ни с какими историческими человеческими построениями, только с фундаментальными законами природы.
|
планковская плотность → планковская плотность (L⁻³M) |
Единицы:
планковская плотность
(L⁻³M)
открыть
свернуть
Плотности различных веществ
Это лишь несколько примеров. Все плотности даны для стандартных условий температур и давления.
| планковская плотность → плотность воздуха на уровне моря | |
| планковская плотность → плотность воды при 0°C | |
| планковская плотность → плотность воды при 4°C | |
| планковская плотность → плотность воды при 100°C | |
| планковская плотность → плотность льда | |
| планковская плотность → плотность алмаза |
| планковская плотность → плотность железа | |
| планковская плотность → плотность меди | |
| планковская плотность → плотность серебра | |
| планковская плотность → плотность свинца | |
| планковская плотность → плотность золота | |
| планковская плотность → плотность платины |
Единицы:
плотность воздуха на уровне моря
/
плотность воды при 0°C
/
плотность воды при 4°C
/
плотность воды при 100°C
/
плотность льда
/
плотность алмаза
/
плотность железа
/
плотность меди
/
плотность серебра
/
плотность свинца
/
плотность золота
/
плотность платины