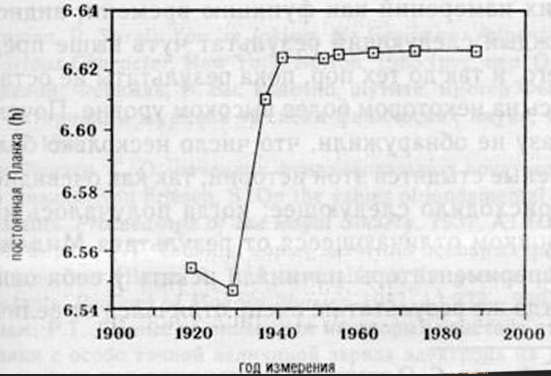
Постоянная планка
Содержание:
Введение и немного обо мне
Жан-Шарль де Бордамоё изобретениепериодический круг (repeating circle)здесьЛюди и измеренияИоганна Георга Траллесаситуации в ШвейцарииЛюдовика XVIКомиссии мер и весовинициативы Шарлеманяle Système international d’unitésПьер-Симон ЛапласАдриен-Мари ЛежандрЖозеф-Луи ЛагранжАнтуан ЛавуазьеМаркиз де КондорсеЖаком-Луи ДавидомМонжЖером ЛаландЛуи Лефеврписалдиссертациюстатье Теодора П. ХиллаДжоном Куинси АдамсомДоклад по мерам и весамmetric menВототкрытой обсерватории LIGOДатчики массы-24крошечные силыастрономии нужны префиксы2410.3931 /е-rarа-28950Лагранжправперевод часов в десятичную систему счисленияДаламберэту статьюбыли прекрасны«À tous les temps, à tous les peuplesТомаса Джефферсонасоздании новых единиц длины и массы
От истоков метрической системы до сегодняшних дней
Жан-Батист-Жозеф ДеламбрПьер Мешенсамой важной миссией, которая когда-либо была поставлена перед человекомМера всех вещейнемецкий фильмчитать о полученных результатах онлайнПарижского меридианаФрансуа АрагоНаполеонаповторное измерение меридианаЛуи Лефевром-Жане3измерений водыкниге УильямсаmetronmetrumЯ-син и Нанкин ЮэМарка-Этьена Жанетакнигу Макдональдса и Хантаулучшает его механические свойстваничего более величественного и простого не выходило из рук человекаmètre étalonэталонов метра:килограммкилометркилогерцМетрической конвенцииДональдом Кнутомкасательно единиц измерения для биологииэто не всерьезНационального института стандартов и технологийраскраскиNCSAпоследний эпизодВозвращение метрологовсуществующую книгуВсемирном дне метрологииМеждународная организация стандартизацииопределяет и описывает11-121-221-1слегка экзотическойУильям ТомсонмемристораqkqkqiqjКарнотеорией Эйнштейнанеизвестнохолодным или более теплым они имеют одинаковую температуруУилларда Гиббсасмежной теме отрицательных температурVфундаментальные константы
Формула Вина и формула Рэлея—Джинса
Теперь пора вернуться к вопросу, который был поставлен в начале статьи: как получить из теории спектральную функцию, которая описывает распределение энергии излучения по спектру, и как она зависит от температуры?
Прежде всего этот вопрос попробовали решить по аналогии, но аналогия с газом не помогла. Число степеней свободы светового потока, как их ни считай, бесконечно велико, и если на каждую степень свободы выделить по одинаковой порции энергии, скажем по kT (световым волнам разумно сопоставить колебательные степени), то общая энергия будет бесконечной при любой конечной температуре. Рассуждение «по аналогии» приводит нас к абсурдному выводу, что вся тепловая энергия стенок (а за ними и всего остального) должна перейти в электромагнитные волны, так что температура всех предметов должна стремиться к абсолютному нулю.
Точные физические измерения говорят, что при каждой температуре тело излучает волны в сравнительно узком интервале спектра. Максимальная энергия излучения сосредоточена вблизи длины волны, которая определяется так называемым законом Вина
Постоянная Вина b = 0,29·10-2 м·К была определена из опыта, но ее происхождение оставалось неясным. Мы увидим дальше, что она связана с постоянной Планка (так же, как и постоянная Стефана — Больцмана).
Закон Вина показывает, что с нагреванием тела максимум спектра смещается в сторону меньших длин волн, т.е. в сторону больших частот (этот закон часто так и называют законом смещения).
Итак, закон Стефана — Больцмана говорит о полной энергии излучения, а закон Вина — о положении максимума в спектре. Другими словами, известно, где спектральная кривая имеет максимум и какова площадь под кривой. Настала очередь обсудить более подробно форму этой кривой.
К началу XX века существовали две формулы, с помощью которых пытались описать форму кривой распределения энергии по спектру. Одну из них предложили два англичанина — это формула Рэлея — Джинса
Сравнение с опытом показало, что формула Рэлея — Джинса правильно описывает спектр только для самых малых частот (слева от максимума кривой).
Если посмотреть на эту формулу с точки зрения числа степеней свободы, то можно дать ей красивое объяснение. Формула Рэлея — Джинса имеет такой вид, как будто участок спектра Δν содержит \(~\frac{8 \pi \nu^2}{c^3}\) степеней свободы, на каждую из которых приходится тепловая энергия kT. Однако эта эффектная интерпретация порочна. Число степеней свободы быстро растет, если переходить ко все большим частотам в ультрафиолетовую часть спектра (направо от максимума кривой). Это значит, что чем больше частота, тем больше энергии содержит спектр, т.е. и по этой формуле все тела должны излучать электромагнитные волны с бесконечно большой энергией.
Этот странный вывод носил драматическое название ультрафиолетовой катастрофы, так как демонстрировал полный провал попыток объяснить свойства спектра, оставаясь в рамках понятий классической физики.
Другую формулу предложил уже известный нам Вин:
(Правда, он писал эту формулу несколько иначе, используя не частоту, а длину волны.) В формуле Вина A и a — некоторые постоянные, связанные, как мы это увидим в дальнейшем, с постоянной Планка. Формула Вина описывала ультрафиолетовую часть спектра, но была беспомощна, когда речь заходила о длинноволновой его части.
Итак, перед работами Планка физики знали уже довольно много: площадь под кривой распределения энергии по спектру, положение максимума и форму кривой в «начале» и в «конце». Оставалось сделать последний смелый шаг. Он-то и привел к рождению новой физики.
Степени свободы
Разница между системой материальных частиц и сплошной средой выступает очень четко, если посмотреть, каким числом координат задается состояние системы.
Положение каждой точки в пространстве задается тремя числами — тремя координатами. Говорят, что материальная точка имеет три степени свободы. Если в систему входит N материальных точек, то говорят, что она имеет 3N степеней свободы.
Такое же рассуждение можно провести и для скоростей. Скорость одной точки описывается тремя числами — тремя компонентами вектора скорости. Скорости N точек требуют для своего описания 3N чисел.
Сколько чисел надо задать, чтобы описать состояние поверхности моря? Строго говоря, для каждой точки поверхности надо задать три числа — вектор скорости воды в данной точке; следовательно, чисел будет бесконечно много. Поверхность моря представляется нам как система с бесконечно большим числом степеней свободы. Даже тот факт, что вода состоит из молекул, а потому число степеней свободы можно определить, сосчитав молекулы, не облегчает задачу: молекул настолько много, что практически число степеней свободы остается бесконечно большим. В действительности же нас не интересует движение каждой молекулы. Когда по морю бегут волны, например от идущего корабля, то мы можем описать картину распределения волн, используя сравнительно немного чисел. Мы можем задавать величину амплитуды и фазы каждой волны; волн хотя и много, но все же меньше, чем молекул. Кроме того, картина, в основном, повторяется со временем: волны более или менее одинаковые.
В каждой волне движется много молекул, движение носит коллективный характер, и мы сможем говорить о коллективных степенях свободы на поверхности моря, в отличие от индивидуальных степеней свободы, скажем, отдельной молекулы воды.
Такое же коллективное описание можно использовать, рассказывая о свойствах света. В частности, мы так и делаем, когда пытаемся описать распределение энергии по спектру.
Свет — волновой процесс, и его описание проще всего выглядит с позиций волновой теории. Конечно, подобное описание света совсем непохоже на описание системы точек. Здесь нет даже намека на какие-то степени свободы — волны и частицы совсем непохожи друг на друга. Но это все-таки не совсем так. У волн и частиц есть общие свойства. Это, прежде всего, те, которые проявляются, когда мы начинаем изучать тепловые явления и думать, как распределяется между волнами и частицами тепловая энергия.
Физические константы, связанные с постоянной Планка
Список
констант, указанных ниже, основан на данных 2014 CODATA. . Приблизительно 90 % неточности в этих
константах связаны с неточностью определения постоянной Планка, как это видно
из квадрата коэффициента корреляции Пирсона (r2 >
0,99, r > 0,995). Если
сравнивать с другими константами, постоянная Планка известна с точностью
порядкапри неопределённости измерения 1σ.Эта
точность значительно лучше, чем у гравитационной
постоянной или у универсальной газовой постоянной.
Масса покоя
электрона
Как
правило, постоянная Ридберга R∞
(в единицах обратной длины) определяется через массу электронаmeи другие физические константы:
Постоянная
Ридберга может быть определена очень точно ()
из спектра атома водорода, тогда как для массы электрона нет прямого способа
измерения. Поэтому для определения массы электрона используется формула:
где c есть скорость света и α есть постоянная
тонкой структуры. Скорость света достаточно точно определяется в системе
единиц СИ, как и постоянная тонкой структуры ().
Поэтому неточность определения массы электрона зависит только от неточности
постоянной Планка (r2 >
0,999).
Постоянная Авогадро
Основная статья: Число Авогадро
Число
Авогадро NA
определяется как отношение массы одного моля электронов к массе одного
электрона. Для её нахождения нужно взять массу одного моля электронов в виде
«относительной атомной массы» электрона Ar(e), измеряемой в ловушке Пеннинга (),
умноженной на единицу молярной массы Mu,
которая в свою очередь определяется как 0,001 кг/моль. В результате
получается:
Зависимость
числа Авогадро от постоянной Планка (r2 >
0,999) повторяется и для других постоянных, связанных с количеством вещества,
например, для атомной единицы массы. Неопределённость в значении постоянной
Планка ограничивает значения атомных масс и частиц в единицах системы СИ, то
есть в килограммах. В то же время отношения масс частиц известны с лучшей
точностью.
Элементарный
заряд
Основная статья: Элементарныйзаряд
Зоммерфельд
первоначально определял постоянную тонкой структуры α так:
где e есть элементарный электрический заряд, ε – электрическая постоянная (называемая также
диэлектрической проницаемостью вакуума), μ
– магнитная постоянная или магнитная проницаемость вакуума. Последние две
постоянные имеют фиксированные значения в системе единиц СИ. Значение α может быть определено экспериментально
путём измерения g-фактора электрона ge
и последующего сравнения со значением, вытекающим из квантовой электродинамики.
В
настоящее время наиболее точное значение элементарного электрического заряда
получается из приведённой выше формулы:
Магнетон
Бора и ядерный магнетон
Основные статьи: Магнетон Бора , Ядерный магнетон
Магнетон
Бора и ядерный магнетон являются единицами, используемыми для описания
магнитных свойств электрона и атомных ядер соответственно. Магнетон Бора есть
магнитный момент, который ожидается у электрона, если бы он вёл себя как
вращающаяся заряженная частица согласно классической электродинамике. Его
значение выводится через постоянную Дирака, элементарный электрический заряд и
массу электрона. Все эти величины выводятся через постоянную Планка,
результирующая зависимость от h½
(r2 > 0,995)
может быть найдена с учётом формулы:
Ядерный магнетон
имеет похожее определение, с той разницей, что протон значительно массивнее
электрона. Отношение электронной относительной атомной массы к протонной
относительной атомной массе может быть определено с большой точностью ().
Для связи между обоими магнетонами можно записать:
ФИЗИКА
Часть 4
Раздел 13 КОРПУСКУЛЯРНЫЕ СВОЙСТВА СВЕТА
13.4. Гипотеза Планка. Формула Планка
Все попытки вывести правильную формулу
для распределения энергии в спектре излучения абсолютно черного тела, исходя
из представлений об атомах как классические осцилляторы, оказались напрасными. Невозможность
объяснить излучения абсолютно черного тела, пользуясь арсеналом
классической физики, было «катастрофой» для нее.
В конце XIX в. среди многих
физиков царило ощущение совершенства и завершенности физической теории.
Правда, выдающийся английский физик В. Томсон указывал на отрицательный результат
опыта А. Майкельсона и на невозможность объяснить излучения абсолютно
черного тела законами классической физики. Как известно, опыт Майкельсона стал
позже экспериментальной основой специальной теории относительности Эйнштейна, а
невозможность объяснить распределение энергии в спектре излучения абсолютно
черного тела законам классической физики привела к возникновению квантовой
механики.
Первым отказался от классических
представлений при решении проблемы излучения абсолютно черного тела М. Планк
(1858 — 1947). В 1900 г. он предложил принципиально новый метод расчета
функции rλ,T, который основывается на квантовых
представлениях. В основу метода был положен гипотезу о том, что тела излучают
энергию не непрерывно, а отдельными порциями, которые получили название квантов. Энергия
в кванта пропорциональна частоте излучения (обратно пропорциональна длине
волны):

где
h = 6,626 ∙ 10-34 Дж ∙
с — постоянная Планка. В механике величина, имеющая размерность произведения энергии на
время, называют действием. В связи с этим постоянную Планка иногда называют квантом действия.
Новые представления Планка о кванты энергии коренным образом изменили взгляды физиков на
элементарные процессы излучения света, а также на все другие процессы в
микромире. Так возникла новая эпоха в учении о строении материи и ее движении.
Руководствуясь представлениями о квантовой
характер теплового излучения, М. Планк получил выражение для
излучательной способности абсолютно черного тела:
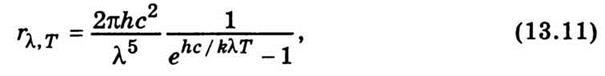
где
с — скорость света в вакууме; k- постоянная Больцмана;
Т — абсолютная
температура; е — основание натуральных логарифмов.
Согласно формуле Планка (13.11) для
каждой длины волны λ с повышением температуры
уменьшается величина еhс/kλТ, что стоит в знаменателе, rλ,T растет. Следовательно, с повышением
температуры увеличивается излучательная способность на всех участках спектра,
причем этот рост разное для различных интервалов длин волн. Именно такая зависимость
rλ,T от температуры наблюдается на
опыте.
Рассмотрим предельные случаи формулы
Планка. В интервале очень длинных волн (λ->∞) энергия отдельного кванта малапо сравнению с энергией теплового движения kT. В этом случае и величину еhс/kλТ можно разложить в ряд Если
учесть только два первых члена разложения, пренебрегая последними, то формула Планка
(13.11) превратится в формулу Рэлея — Джинса (13.8).
Во втором предельном случае очень коротких волн и
в знаменателе (13.11) можно пренебречь единицей по сравнению с первым членом. Тогда
формула Планка будет сводиться к формуле Вина (13.7), которая хорошо опишет участок
спектра в интервале малых длин волн.
В отличие от формулы Вина и Рэлея
— Джинса формула Планка хорошо согласуется с
экспериментом во всем интервале длин волн и всех температур. При
интегрировании по всем длинам волн из формулы Планка можно получить закон Стефана — Больцмана, а не бесконечность, как это было в
случае формулы Рэлея — Джинса.
Наконец, по правилам отыскания
максимума функции из формулы Планка обычными методами дифференциального
счисления можно вывести закон смещения Вина. Благодаря формуле Планка можно
определить также все другие закономерности излучения абсолютно черного тела.
Следует отметить, что, исходя из
формулы Планка для лучеиспускательной способности абсолютно черного тела, можно
достать не только внешнюю форму соответствующего закона, но и определить постоянную Стефана — Больцмана σ и постоянная закона смещения Вина b через универсальные стали h, k, с
т.д. Исчисленные таким
образом стали σ и b совпадают с их эмпирическим значением. Все это
приводит к выводу, что формула Планка наиболее полно характеризует тепловое
излучения.
Формула Планка имеет большое значение
не только в теории теплового излучения, но и в установлении современных взглядов
на строение материи и ее движении.
| Назад | Вперед |
История открытия
Формула Планка для теплового излучения
Основная статья: Формула Планка
Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком для равновесной плотности излучения u(ω,T){\displaystyle u(\omega ,T)}. Формула Планка была получена после того, как стало ясно, что формула Рэлея — Джинса удовлетворительно описывает излучение только в области длинных волн. В 1900 году Планк предложил формулу с постоянной (впоследствии названной постоянной Планка), которая хорошо согласовывалась с экспериментальными данными. При этом Планк полагал, что данная формула является всего лишь удачным математическим трюком, но не имеет физического смысла. То есть Планк не предполагал, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с циклической частотой излучения выражением:
- ε=ℏω.{\displaystyle \varepsilon =\hbar \omega .}
Коэффициент пропорциональности ħ впоследствии назвали постоянной Планка, ħ ≈ 1,054·10−34 Дж·с.
Фотоэффект
Основная статья: Фотоэффект
Фотоэффект — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Озеена, получил Нобелевскую премию) на основе гипотезы Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии, при представлении света в виде частиц (фотонов), следует формула Эйнштейна для фотоэффекта:
- ℏω=Aout+mv22,{\displaystyle \hbar \omega =A_{out}+{\frac {mv^{2}}{2}},}
где Aout{\displaystyle A_{out}} — т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества), mv22{\displaystyle {\frac {mv^{2}}{2}}} — кинетическая энергия вылетающего электрона, ω{\displaystyle \omega } — частота падающего фотона с энергией ℏω,{\displaystyle \hbar \omega ,} ℏ{\displaystyle \hbar } — постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из тела. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества, то есть на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.
Почему основных единиц измерения именно 7?
Гауссувыразить массувремя и длинуКантоммаксимально могут изменяться-18е2hэтуэту статьиμ-72hμααμволнового сопротивления вакуума ZБриджменЮлиус ВаллотЯн де БурЭдвард ГуггенхаймДжованни ДжорджиОтто ГёльдерРудольф ФлейшманнУльрих ШтиллеХасслер Уитнивероятность физической величинойРичарда фон МизесаРейхенбахакак раньшевекторную дифференциацию физических единицобщей структуре систем единиц измеренияразбирательствах в ДагштулеКлодом ШеннономСилардSP 811Однаконе отметитьэксперты обсуждаютдеталяхМикеланджелоДавиду3423-113повторным анализом Божественной комедии ДантеG(mе / (hк))1/2 Sinfonia de motuВойцеха КиляраРилькеСтатус единицы измерения
Спектральная функция
Спектральная функция f(ν) — это, вероятно, самое трудное, что нужно понять в этой статье. Спектр, который мы видим на экране, тянется непрерывной полоской, и в нем представлены все частоты. Не имеет смысла спрашивать, какую энергию можно сопоставить в спектре точно данной частоте ν. Когда из источника течет вода, нельзя спросить, сколько воды вытечет в какой-то определенный момент времени, например ровно в 12 часов дня. Точно в этот момент вытекает объем воды, равный нулю. Для того чтобы вытекло какое- то количество воды, надо, чтобы прошел хотя бы небольшой промежуток времени. Можно спросить, сколько воды вытечет за время от 12.00 до 12.01. Можно спросить, сколько вытечет воды за любой интервал времени Δt от 12 часов до 12 часов + Δt минут. Если вода течет более или менее равномерно и за 1 минуту вытекает g см3 воды, то за время Δt вытечет g(t)Δt см3.
Мы написали не g а g(t), так как в разное время (в час дня, в два часа дня и т.д.) вода может течь по-разному. Это, например, означает, что количество воды, вытекающее за 1 минуту в 12.15, и количество воды, вытекающее за 1 минуту в 12.30, относятся как g(15) : g(30), если за начало отсчета времени взять полдень — 12.00.
При подсчете количества воды мы сталкиваемся с новой величиной, которая описывает интенсивность непрерывного процесса, — g есть отношение количества воды, вытекающего за интервал времени Δt, к этому интервалу, когда он взят очень маленьким.
Спектральная функция имеет аналогичный смысл: она определяет отношение энергии в полоске спектра к ширине этой полоски, когда ширина полоски взята очень маленькой. Ширина при этом измеряется, как было уже сказано, не в длинах, а в частотах.
Вывод для абсолютно чёрного тела
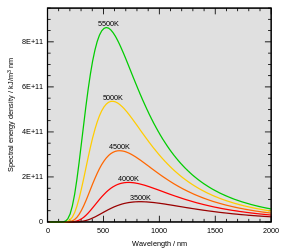 Излучение абсолютно чёрного тела
Излучение абсолютно чёрного тела
Вследствие линейности уравнений электромагнитного поля, любое их решение может быть представлено в виде суперпозиции монохроматических волн; каждая — с определённой угловой частотой ω{\displaystyle \omega }. Энергия поля может быть представлена как сумма энергий соответствующих полевых осцилляторов. Как известно из квантовой механики, энергия осциллятора принимает дискретные значения, согласно следующей формуле:
- En=ℏω(n+12).{\displaystyle E_{n}=\hbar \omega (n+1/2).}
Поскольку рассматривается равновесное излучение, то, используя каноническое распределение Гиббса, можно определить вероятность состояния осциллятора с заданной энергией:
- Wn=1Z⋅exp(−EnkT).{\displaystyle W_{n}={1 \over Z}\cdot \mathrm {exp} \left(-{E_{n} \over kT}\right).}
Статистическая сумма Z{\displaystyle Z} равна:
- Z=∑exp(−ℏωkT⋅(n+12))=exp(−ℏω2kT)⋅∑exp(−ℏωkT)n=exp(−ℏω2kT)1−exp(−ℏωkT).{\displaystyle Z=\sum \mathrm {exp} \left(-{\hbar \omega \over {kT}}\cdot (n+1/2)\right)=\mathrm {exp} \left(-{{\hbar \omega } \over {2kT}}\right)\cdot \sum \mathrm {exp} \left(-{{\hbar \omega } \over {kT}}\right)^{n}={\frac {\mathrm {exp} \left(-{{\hbar \omega } \over {2kT}}\right)}{1-\mathrm {exp} \left(-{{\hbar \omega } \over {kT}}\right)}}.}
Свободная энергия Ψ{\displaystyle \Psi } равна:
- Ψ=−kT⋅lnZ=ℏω2+kT⋅ln(1−exp(−ℏωkT)).{\displaystyle \Psi =-kT\cdot \ln Z={\frac {\hbar \omega }{2}}+kT\cdot \ln \left(1-\mathrm {exp} \left(-{\hbar \omega \over kT}\right)\right).}
Для средней (математическое ожидание) энергии ε¯{\displaystyle {\overline {\varepsilon }}} воспользуемся уравнением Гиббса — Гельмгольца:
- ε¯=∑(WnEn)=Ψ−(kT⋅∂(Ψ)∂(kT))=(kT)2⋅∂(lnZ)∂(kT)=(kT)2⋅(ℏω2(kT)2+exp(−ℏωkT)⋅ℏω(kT)21−exp(−ℏωkT)){\displaystyle {\overline {\varepsilon }}=\sum (W_{n}E_{n})=\Psi -\left(kT\cdot {\frac {\partial (\Psi )}{\partial (kT)}}\right)=(kT)^{2}\cdot {\frac {\partial (\ln Z)}{\partial (kT)}}=(kT)^{2}\cdot \left({\frac {\hbar \omega }{2(kT)^{2}}}+{\frac {\mathrm {exp} \left(-{{\hbar \omega } \over {kT}}\right)\cdot {\hbar \omega \over (kT)^{2}}}{1-\mathrm {exp} \left(-{\hbar \omega \over kT}\right)}}\right)};
таким образом — средняя энергия ε¯{\displaystyle {\overline {\varepsilon }}}, приходящаяся на полевой осциллятор, равна:
| ε¯=ℏω2+ℏωexp(ℏωkT)−1{\displaystyle {\overline {\varepsilon }}={\frac {\hbar \omega }{2}}+{\frac {\hbar \omega }{\mathrm {exp} \left({\hbar \omega \over kT}\right)-1}}}, | (1) |
где ℏ{\displaystyle \hbar } — постоянная Планка, k{\displaystyle k} — постоянная Больцмана.
Количество же стоячих волн в единице объёма в трёхмерном пространстве, в интервале (ω;ω+dω){\displaystyle (\omega ;\omega +d\omega )}, равно:
| dnω=ω2dωπ2c3{\displaystyle \mathrm {d} n_{\omega }={\frac {\omega ^{2}\mathrm {d} \omega }{\pi ^{2}c^{3}}}}. | (2) |
Следовательно, для спектральной плотности мощности электромагнитного излучения получаем:
- u(ω,T)=ε¯dnωdω=ℏω32π2c3+ℏω3π2c3(exp(ℏωkT)−1),{\displaystyle u(\omega ,T)={\overline {\varepsilon }}{\frac {\mathrm {d} n_{\omega }}{\mathrm {d} \omega }}={\frac {\hbar {\omega }^{3}}{2\pi ^{2}c^{3}}}+{\frac {\hbar {\omega }^{3}}{\pi ^{2}c^{3}\left(\mathrm {exp} \left({\hbar \omega \over kT}\right)-1\right)}},}
где первое слагаемое связано с энергией нулевых колебаний, а второе — это и есть формула Планка.
Формулу Планка также можно записать и через длину волны:
| up(λ,T)=4π2ℏc2λ5(exp(2πλℏckT)−1){\displaystyle u_{p}(\lambda ,T)={\frac {4\pi ^{2}\hbar c^{2}}{\lambda ^{5}\left(\mathrm {exp} \left({{2\pi \over \lambda }{\hbar c \over kT}}\right)-1\right)}}}. | (5) |
Вывод, исходя из распределения Бозе — Эйнштейна
Фотоны являются бозонами и подчиняются статистике Бозе — Эйнштейна. Для этой статистики, среднее число частиц с данной энергией ε{\displaystyle \varepsilon } равно:
- n¯(ε)=1exp(εΘ)−1.{\displaystyle {\overline {n}}(\varepsilon )={\frac {1}{\mathrm {exp} ({\varepsilon /\Theta })-1}}.}
По определению:
- u(ε)dε=εn(ε)dN(ε),{\displaystyle u(\varepsilon )\mathrm {d} \varepsilon =\varepsilon n(\varepsilon )\mathrm {d} N(\varepsilon ),}
где dN=ε2dεπ2c3ℏ3{\displaystyle \mathrm {d} N={\frac {\varepsilon ^{2}\mathrm {d} \varepsilon }{\pi ^{2}c^{3}\hbar ^{3}}}} — число осцилляторов (в единице объёма) электромагнитного поля с данной энергией, в бесконечно малой окрестности ε=ℏω{\displaystyle \varepsilon =\hbar \omega }.
Подставив формулу среднего числа бозонов с данной энергией в эту формулу, получим формулу Планка.
Итог
В стандартной модели Вселенной самая высокая из когда-либо зафиксированных температур была достигнута за доли секунды после Большого взрыва. В течение этого незначительного периода времени излучаемый свет имел длину волны 10 ^ -35 метров. Эта длина называется длиной Планка и является наименьшей измеримой длиной во Вселенной. Из-за этой небольшой длины волны температура достигала 1,416808·1032 кельвинов, или 142 квинтиллиона кельвинов (142 ниллионда по короткой шкале), что называется температурой Планка и является самым близким определением «абсолютной жары», которое мы имеем в настоящее время.
Помимо того, что температура Планка является самой высокой температурой, когда-либо теоретически достигнутой в нашей Вселенной, физики предполагают, что при любой температуре, превышающей стандарт Планка, гравитационные силы затронутых частиц станут настолько сильными, что они могут создать черную дыру. Черная дыра, которая создается из энергии, а не из материи, называется «кугельблиц». Наши общепринятые в настоящее время модели физики рушатся на фоне этого явления, оставляя многие вопросы без ответа.
Если вы что-то не поняли, предлагаем посмотреть этот ролик, из которого вы обязательно поймете многие вещи по этой теме:
https://youtube.com/watch?v=XEHbL3bnIbU