Корпускулярно-волновой дуализм

Импульс фотона

Импульс фотона:

Давление света

Максвелл на основе электромагнитной теории света предсказал, что свет должен оказывать давление на препятствия.

Под действием электрического поля волны, падающей на поверхность тела, например металла, свободный электрон движется в сторону, противоположную вектору ​\( \vec{E} \)​.

На движущийся электрон действует сила Лоренца, направленная в сторону распространения волны. Суммарная сила, действующая на электроны поверхности металла, и определяет силу светового давления.

Для доказательства справедливости теории Максвелла было важно измерить давление света. Многие ученые пытались это сделать, но безуспешно, так как световое давление очень мало

В яркий солнечный день на поверхности площадью 1 м2 действует сила, равная всего лишь 4·10-6 Н.

Впервые давление света измерил русский физик Петр Николаевич Лебедев в 1900 г. Прибор Лебедева состоял из очень легкого стерженька на тонкой стеклянной нити, по краям которого были приклеены легкие крылышки. Весь прибор помещался в сосуд, откуда был выкачан воздух. Свет падал на крылышки, расположенные по одну сторону от стерженька. О значении давления можно было судить по углу закручивания нити. Трудность точного измерения давления света была связана с невозможностью создать вакуум (движение молекул воздуха, вызванное неодинаковым нагревом крылышек и стенок сосуда, приводит к возникновению дополнительных вращающих моментов). На закручивание нити влияет и неодинаковый нагрев сторон крылышек (сторона, обращенная к источнику света, нагревается сильнее, чем противоположная сторона). Молекулы, отражающиеся от более нагретой стороны, передают крылышку больший импульс, чем молекулы, отражающиеся от менее нагретой стороны.

Лебедев сумел преодолеть все эти трудности, взяв очень большой сосуд и очень тонкие крылышки. Полученное значение совпало с предсказанным Максвеллом. Впоследствии после трех лет работы Лебедеву удалось осуществить еще более тонкий эксперимент: измерить давление света на газы.

Появление квантовой теории света позволило более просто объяснить причину светового давления. Фотоны, подобно частицам вещества, имеющим массу покоя, обладают импульсом. При поглощении их телом они передают ему свой импульс. Согласно закону сохранения импульса импульс тела становится равным импульсу поглощенных фотонов. Поэтому покоящееся тело приходит в движение. Изменение импульса тела означает, согласно второму закону Ньютона, что на тело действует сила.

Важно! Опыты Лебедева можно рассматривать как экспериментальное доказательство того, что фотоны обладают импульсом. Хотя световое давление очень мало в обычных условиях, оно является существенным в недрах звезд

При температуре в несколько десятков миллионов Кельвинов давление электромагнитного излучения достигает громадных значений и совместно с гравитационными силами обеспечивает стабильное состояние звезд

Хотя световое давление очень мало в обычных условиях, оно является существенным в недрах звезд. При температуре в несколько десятков миллионов Кельвинов давление электромагнитного излучения достигает громадных значений и совместно с гравитационными силами обеспечивает стабильное состояние звезд.

Давление света, согласно электродинамике Максвелла, возникает из-за действия силы Лоренца на электроны среды, колеблющиеся под действием электрического поля электромагнитной волны. С точки зрения квантовой теории давление появляется в результате передачи телу импульсов фотонов при их поглощении:

где ​\( \rho \)​ – коэффициент отражения, ​\( N \)​ – количество всех фотонов, падающих на единицу поверхности в единицу времени.

Примечания[править]

1. http://e-science.ru/physics/theory/?t=12
2. http://fn.bmstu.ru/phys/bib/physbook/tom5/ch1/texthtml/ch1_5.htm
3. Фок В. А., Теория пространства, времени и тяготения. — M.: Наука, 1972
4. Фейнман Р., Хибс А. Квантовая механика и интегралы по траекториям. — М.: 1968. — 384 с.о книге
5. Борн, М. Атомная физика. — М.: «Мир», 1965. — С. 389.о книгеСвойство «Ссылка/Автор» типа «Страница» со значением «Борн, М.» содержит недопустимые символы или неполно и может привести к неожиданным результатам при семантическом аннотировании или запросе.
6. Taylor, G. I. (1909). «Interference fringes with feeble light». Proceedings of the Cambridge Philosophical Society 15: 114—115.
7. Experimental Evidence for a Photon Anticorrelation Effect on a Beam Splitter: A New Light on Single-Photon Interferences

Опыты А. Г. Столетова

В 1888 году А. Г. Столетов впервые систематически исследовал фотоэффект. Он выяснил, от чего зависит число вырванных светом с поверхности вещества электронов (фотоэлектронов) и чем определяется их скорость или кинетическая энергия. Он исследовал вещества различной природы и установил, что наиболее восприимчивы к свету металлы: никель, медь, цинк, алюминий, серебро. Для облучения электродов он использовал свет различных длин волн: красный, зеленый, синий, ультрафиолетовый.

Для исследования фотоэффекта он собрал следующую установку: в стеклянный баллон, из которого выкачан воздух, помещаются два электрода.

Внутрь баллона на один из электродов поступает свет через кварцевое «окошко», прозрачное для ультрафиолетового излучения.

На электроды подается напряжение, которое можно менять с помощью потенциометра ​\( R \)​ и измерять вольтметром ​\( V \)​.

К освещаемому электроду (катоду ​\( K \)​) присоединяют отрицательный полюс батареи. Под действием света этот электрод испускает электроны, которые при движении в электрическом поле образуют электрический ток.

Облучая катод светом различных длин волн, Столетов установил закономерности (законы) фотоэффекта, не утратившие своего значения до нашего времени.

При малых напряжениях не все вырванные светом электроны достигают другого электрода (анод А). Если, не меняя интенсивности излучения, увеличивать разность потенциалов между электродами, то сила тока также увеличивается. При некотором напряжении она достигает максимального значения, после чего перестает изменяться.

Вольт-амперная характеристика (зависимость силы фототока от напряжения)

Из графика видно:

1) сила фототока отлична от нуля и при отсутствии напряжения. Это означает, что часть вырванных светом электронов достигает анода и при отсутствии напряжения, т. е. фотоэлектроны при вылете обладают кинетической энергией;

2) при некотором значении напряжения ​\( U_{нас} \)​ между электродами сила фототока перестает зависеть от напряжения и не изменяется при увеличении напряжения. Максимальное значение силы тока \( I_{нас} \) называется током насыщения. При фототоке насыщения все электроны, покинувшие за 1 с поверхность металла, за это же время попадают на анод. Поэтому по силе фототока насыщения можно судить о числе фотоэлектронов, вылетающих с катода в единицу времени:

где ​\( q_{max} \)​ – максимальный заряд, переносимый фотоэлектронами; ​\( n \)​ – число фотоэлектронов, вылетающих с поверхности освещаемого металла; ​\( e \)​ – заряд электрона;

3) если катод соединить с положительным полюсом источника тока, а анод — с отрицательным, то в электростатическом поле между электродами фотоэлектроны будут тормозиться, а сила фототока уменьшаться при увеличении значения этого отрицательного напряжения. При некотором значении отрицательного напряжения ​\( U_{зап} \)​ (его называют запирающим или задерживающим напряжением) фототок прекращается. Это значит, что электрическое поле тормозит вырванные электроны до полной остановки, а затем возвращает их на электрод.

Согласно теореме о кинетической энергии работа задерживающего электрического поля равна изменению кинетической энергии фотоэлектронов:

Законы внешнего фотоэффекта

• Закон Столетова: количество электронов, выбиваемых светом с поверхности металла за 1 с, прямо пропорционально интенсивности света и не зависит от частоты падающего света.
• Максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения, а определяется только его частотой.
• Для каждого вещества существует «красная граница» фотоэффекта, т. е. минимальная частота света, ниже которой фотоэффект невозможен.

«Красная граница» фотоэффекта – наименьшая частота (наибольшая длина волны), при которой начинается фотоэффект:

С уменьшением частоты падающего света (увеличением длины волны) энергия падающих квантов при некоторой частоте (длине волны) может стать равной работе выхода электрона из металла.

«Красная граница» фотоэффекта зависит только от работы выхода электрона из вещества.

Фотоэффект практически безынерционен. Он наступает через 10-9 с от момента освещения катода.

Элементы квантовой механики Править

Физика атомов, молекул и их коллективов, в частности кристаллов, а также атомных ядер и элементарных частиц изучается в квантовой механике. Объекты микромира, изучаемые квантовой механикой, имеют линейные размеры порядка $ 10^{-6}\ldots 10^{-13} $ см. Если частицы движутся со скоростями много меньше, чем скорость света в вакууме $ c $, то применяется нерелятивистская квантовая механика; при скоростях близких к $ c $ — релятивистская квантовая механика.

В основе квантовой механики лежат представления Планка о дискретном характере изменения энергии атомов, Эйнштейна о фотонах, данные о квантованности некоторых физических величин (например, импульса и энергии), характеризующих в определенных условиях состояния частиц микромира.
Основополагающей в квантовой механике явилась идея о том, что корпускулярно-волновая двойственность свойств, установленная для света, имеет универсальный характер. Она должна проявляться для любых частиц, обладающих импульсом $ p $. Все частицы, имеющие конечный импульс $ p $, обладают волновыми свойствами, и их движение сопровождается некоторым волновым процессом.

Формула де Бройля устанавливает зависимость длины волны $ \lambda $, связанной с движущейся частицей вещества, от импульса $ p $ частицы:

$ \lambda=\frac{h}{p}=\frac{h}{mv}, $

где $ m $ — масса частицы, $ v $ — ее скорость, $ h $ — постоянная Планка. Волны, о которых идет речь, называются волнами де Бройля.

Другой вид формулы де Бройля:

$ \mathbf{p}=\frac{h}{2\pi}\mathbf{k}=\hbar\mathbf{k}, $

где $ \mathbf{k}=\frac{2\pi}{\lambda}\mathbf{n} $ — волновой вектор, модуль которого $ k=\frac{2\pi}{\lambda} $ — волновое число — есть число длин волн, укладывающихся на $ 2\pi $ единицах длины, $ \mathbf{n} $ — единичный вектор в направлении распространения волны, $ \hbar=\frac{h}{2\pi}=1{,}05\cdot 10^{-34} $ Дж·с.

Длина волны де Бройля для частицы с массой $ m $, имеющей кинетическую энергию $ W_k $

$ \lambda=\frac{h}{\sqrt{2mW_k}}. $

В частности, для электрона, ускоряющегося в электрическом поле с разностью потенциалов $ \Delta\varphi $ вольт

$ \lambda=\frac{12{,}25}{\sqrt{\Delta\varphi}}\;\overset{\circ}{\mathrm{A}}. $

Формула де Бройля экспериментально подтверждается опытами по рассеянию электронов и других частиц на кристаллах и по прохождению частиц сквозь вещества. Признаком волнового процесса во всех таких опытах является дифракционная картина распределения электронов (или других частиц) в приемниках частиц.

Волновые свойства не проявляются у макроскопических тел. Длины волн де Бройля для таких тел настолько малы, что обнаружение волновых свойств оказывается невозможным.

Фазовая скорость волн де Бройля свободной частицы

$ v_f=\frac{\omega}{k}=\frac{c^2}{v}=\frac{c^2}{h}m\lambda=\frac{c^2p^2}{2Wh}\lambda, $

где $ \omega=2\pi\nu $ — циклическая частота, $ W $ — энергия свободной частицы, $ p=mv $ — импульс частицы, $ m $ — ее масса, $ v $ — ее скорость, $ \lambda $ — длина дебройлевской волны. Зависимость фазовой скорости дебройлевских волн от длины волны указывает на то, что эти волны испытывают дисперсию.

Групповая скорость волн де Бройля равна скорости частицы $ u $:

$ u=\frac{d\omega}{dk}=v. $

Связь между энергией частицы $ W $ и частотой $ \nu $ волны де Бройля

$ W=h\nu=\hbar\omega, $

Волны де Бройля имеют специфическую природу, не имеющую аналогии среди волн, изучаемых в классической физике: квадрат модуля амплитуды волны де Бройля в данной точке является мерой вероятности того, что частица обнаруживается в этой точке. Дифракционные картины, которые наблюдаются в опытах, являются проявлением статистической закономерности, согласно которой частицы попадают в определенные места в приёмниках — туда, где интенсивность волны де Бройля оказывается наибольшей. Частицы не обнаруживаются в тех местах, где, согласно статистической интерпретации, квадрат модуля амплитуды «волны вероятности» обращается в нуль.

Волны де Бройля

Основная статья: Волны де Бройля

Количественное выражение принцип корпускулярно-волнового дуализма получает в идее волн де Бройля. Для любого объекта, проявляющего одновременно волновые и корпускулярные свойства, имеется связь между импульсом p{\displaystyle \mathbf {p} } и энергией E{\displaystyle E}, присущими этому объекту как частице, и его волновыми параметрами — волновым вектором k{\displaystyle \mathbf {k} }, длиной волны λ{\displaystyle \lambda }, частотой ν{\displaystyle \nu }, циклической частотой ω{\displaystyle \omega }. Эта связь задаётся соотношениями:

p=ℏk; |p|=hλ,{\displaystyle \mathbf {p} =\hbar \mathbf {k} ;\ |\mathbf {p} |=h/\lambda ,}

E=ℏω=hν,{\displaystyle E=\hbar \omega =h\nu ,}

где ℏ{\displaystyle \hbar } и h=2πℏ{\displaystyle h=2\pi \hbar } — редуцированная и обычная постоянная Планка, соответственно. Эти формулы верны для релятивистских энергии и импульса.

Волна де Бройля ставится в соответствие любому движущемуся объекту микромира; таким образом, в виде волн де Бройля и свет, и массивные частицы подвержены интерференции и дифракции. В то же время чем больше масса частицы, тем меньше её дебройлевская длина волны при той же скорости, и тем сложнее зарегистрировать её волновые свойства. Грубо говоря, взаимодействуя с окружением, объект ведёт себя как частица, если длина его дебройлевской волны много меньше характерных размеров, имеющихся в его окружении, и как волна — если много больше; промежуточный случай может быть описан только в рамках полноценной квантовой теории.

Физический смысл волны де Бройля таков: квадрат модуля амплитуды волны в определённой точке пространства равен плотности вероятности обнаружения частицы в данной точке, если будет проведено измерение её положения. В то же время, пока измерение не проведено, частица в действительности не находится в каком-либо одном конкретном месте, а «размазана» по пространству в виде дебройлевской волны.

Идея волны де Бройля как эмпирическая закономерность помогает делать общие выводы о том, будут ли в той или иной ситуации проявляться волновые свойства массивных частиц, и получать количественные оценки в простых случаях — например, оценить ширину дифракционных полос при дифракции электронов. Но эта идея не описывает реальность непосредственно и не позволяет полностью правильно описать поведение частиц с учётом всех основных эффектов квантовой механики (например, квантовая запутанность). Поэтому в основе математического описания (нерелятивистской) квантовой механики лежит другой, более корректно и строго определённый объект с похожим смыслом — волновая функция.

Фотоэффект

Фотоэффект был открыт в 1887 году Г. Герцем.

В опытах с электроискровыми вибраторами Герц установил, что заряженный проводник, освещенный ультрафиолетовыми лучами, быстро теряет свой заряд, а электрическая искра возникает в искровом промежутке при меньшей разности потенциалов.

Фотоэффект – это явление взаимодействия света с веществом, в результате которого энергия фотонов передается электронам вещества.

Различают внутренний и внешний фотоэффект.

Внутренний фотоэффект – изменение концентрации носителей заряда в веществе.

Внешний фотоэффект – явление вырывания электронов с поверхности вещества под действием падающего на него света.

История развития

Основная статья: История квантовой механики

Вопросы о природе света и вещества имеют многовековую историю, однако до определённого времени считалось, что ответы на них обязаны быть однозначными: свет — либо поток частиц, либо волна; вещество либо состоит из отдельных частиц, подчиняющихся классической механике, либо представляет собой сплошную среду.

Атомно-молекулярное учение на протяжении своего развития долго оставалось в статусе лишь одной из возможных теорий, однако к концу XIX века существование атомов и молекул уже не вызывало сомнений. В 1897 году Томсон экспериментально обнаружил электрон, а в 1911 году Резерфорд открыл ядро атома. Была разработана боровская модель атома, в которой электрон подразумевался точечной или очень малой частицей. Однако модель Бора была не вполне последовательна, требовалась другая теория.

Что же касается света, то корпускулярная теория света, представляющая световой луч как поток отдельных частиц, была популярна в Новое время — самым известным из её сторонников был внёсший большой вклад в изучение света Исаак Ньютон. Однако в XIX веке были сформулированы принцип Гюйгенса — Френеля и затем уравнения Максвелла, прекрасно описывавшие свет как волну, состоящую из колебаний электромагнитного поля. Взаимодействие электромагнитной волны с веществом успешно описывалось классической теорией поля.

Казавшееся устоявшимся волновое описание света оказалось неполным, когда в 1901 году Планк получил формулу для спектра излучения абсолютно чёрного тела, а затем Эйнштейн объяснил фотоэффект, опираясь на предположение, что свет с определённой длиной волны излучается и поглощается исключительно определёнными порциями. Такая порция — квант света, позднее названный фотоном, — переносит энергию, пропорциональную частоте световой волны с коэффициентом h{\displaystyle h} — постоянная Планка. Таким образом, оказалось, что свет проявляет не только волновые, но и корпускулярные свойства.

Французский учёный Луи де Бройль (1892—1987), развивая представления о двойственной корпускулярно-волновой природе света, выдвинул в 1923 году гипотезу об универсальности корпускулярно-волнового дуализма. Он утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами.

Согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики — энергия E{\displaystyle E} и импульс p{\displaystyle p}, а с другой стороны — волновые характеристики — частота и длина волны.

Более конкретное и корректное воплощение принцип корпускулярно-волнового дуализма получил в «волновой механике» Шрёдингера, которая затем превратилась в современную квантовую механику.

Вскоре Джордж Томсон и Клинтон Джозеф Дэвиссон с Лестером Джермером независимо обнаружили дифракцию электронов, дав тем самым убедительное подтверждение реальности волновых свойств электрона и правильности квантовой механики.

Так как дифракционная картина исследовалась для потока электронов, то необходимо было доказать, что волновые свойства присущи каждому электрону в отдельности. Это удалось экспериментально подтвердить в 1948 году советскому физику В. А. Фабриканту. Он показал, что даже в случае столь слабого электронного пучка, когда каждый электрон проходит через прибор независимо от других, возникающая при длительной экспозиции дифракционная картина не отличается от дифракционных картин, получаемых при короткой экспозиции для потоков электронов в десятки миллионов раз более интенсивных.

Трактовку корпускулярно-волнового дуализма в русле квантовой механики дал физик В. А. Фок (1898—1974):

Ричард Фейнман в ходе построения квантовой теории поля развил общепризнанную сейчас формулировку через интегралы по траекториям, которая не требует использования классических понятий «частицы» или «волны» для описания поведения квантовых объектов.

Природа света[править]

Световая волна представляет собой нелокализованное электромагнитное поле, распределенное по пространству. Объемная плотность энергии электромагнитного поля волны, пропорциональная квадрату ее амплитуды, может изменяться на сколь угодно малую величину, то есть непрерывно.

Свет можно трактовать как поток корпускул (квантов, фотонов), которые во многих физических эффектах проявляют свойства . Свет демонстрирует свойства волны в явлениях дифракции и интерференции при масштабах, сравнимых с длиной световой волны. Например, даже одиночные фотоны, проходящие через двойную щель, создают на экране интерференционную картину, определяемую уравнениями Максвелла.

Экспериментально показано, что фотон не является коротким импульсом электромагнитного излучения. Он не может быть разделён на несколько пучков оптическими делителями лучей, что наглядно показал эксперимент, проведённый французскими физиками Гранжье, Роже и Аспэ в 1986 году. Корпускулярные свойства света проявляются при фотоэффекте и в эффекте Комптона. Фотон ведет себя и как частица, которая излучается или поглощается целиком объектами, размеры которых много меньше его длины волны (например, атомными ядрами), или вообще могут считаться точечными (например, электрон).

Не имеет значение в какой области рассматривать свет. Например, в области зрения и цветного зрения, свет выполняет функции как волны так и частицы — кванта энергии (фотона). Сфокусированная предметная точка на фоторецептор сетчатки, например, мембрану колбочки позволяет глазу отфильтровать, сформировать её значение в виде основных спектральных лучей света RGB согласно их длинам волн, и согласно значениям квантов энергии монолучей (не в цвете), которые в мозгу переводятся в наше ощущение цвета (сфокусированной предметной точки оптического изображения).

Природа света с точки зрения диалектикиправить

С точки зрения диалектической, современная физика отвечает на вопрос о природе света так: свет есть материальный объект, обладающий как волновыми, так и корпускулярными свойствами. Эти свойства в различных физических процессах могут проявляться на различном уровне.

Природа света с точки зрения оптическойправить

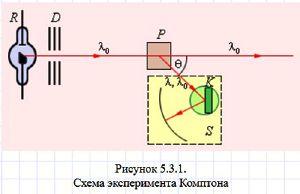
Рис.2. Опыт Комптона. на первом этапе рассеяния излучения на мишени оно ведет себя как поток фотонов, но в измерительном блоке это же излучение как электромагнитная волна испытывает дифракцию на кристаллической решетке.

При определенных условиях, например, в ряде оптических явлений свет проявляет свои свойства как волна. В данных случаях должны рассматривать свет как электромагнитные волны. В других оптических явлениях свет проявляет свои свойства как свойства частиц (корпускулярные). В этом случае свет следует представлять как поток фотонов (квантов). Иногда, оптический эксперимент можно организовать так, что свет будет проявлять в нем как волновые, так и корпускулярные свойства. Действительно, в опыте Комптона (см. рис. 2) на первом этапе рассеяния излучения на мишени оно ведет себя как поток фотонов, но в измерительном блоке это же излучение как электромагнитная волна испытывает дифракцию на кристаллической решетке.

Дифракция электронов

Дифракция электронов является опытным доказательством гипотезы де Бройля о волновых свойствах частиц.

Опыт К. Дэвиссона и Л. Джермера (1927)

Общим условием дифракции является соизмеримость длины падающей волны с расстоянием между рассеивающими центрами: ​\( \lambda\approx d \)​.

В качестве дифракционной решетки использовалась кристаллическая решетка никеля, расстояние между атомами которого ​\( d \)​ ≈ 2·10-10 м. Пучок ускоренных электрическим полем электронов с длиной волны ​\( \lambda \)​ ≈ 10-10 м направлялся под углом ​\( \varphi \)​ на поверхность кристалла никеля. Полученная дифракционная картина и явилась доказательством наличия у электронов волновых свойств.