Гелий he

Альфа-распад

При альфа-распаде излучается α-частица (ядро

атома гелия). Из вещества с количеством протонов Z и нейтронов N в атомном ядре оно превращается в вещество с количеством протонов Z-2 и количеством нейтронов N-2, атомной массой А-4. То есть происходит смещение образовавшегося элемента на две клетки назад в периодической системе.

Альфа-распад – это внутриядерный процесс. В составе тяжелого ядра за счет сложной картины сочетания ядерных и электростатических сил образуется самостоятельная α-частица, которая выталкивается кулоновскими силами гораздо активнее остальных нуклонов. При определенных условиях она может преодолеть силы ядерного взаимодействия и вылететь из ядра.

Физика8 класс

§ 29. Строение атомов

Атомы разных элементов в обычном состоянии отличаются друг от друга числом электронов, движущихся вокруг ядра. Так, в атоме водорода вокруг ядра движется один электрон, в атоме гелия — два электрона. Есть атомы с тремя, четырьмя электронами и т. д. Вокруг ядра атома кислорода движется 8 электронов, железа — 26, урана — 92 электрона.

Но всё же главной характеристикой данного химического элемента является не число электронов, а заряд ядра.

Дело в том, что электроны могут иногда отрываться от атома и тогда общий заряд электронов в атоме изменится. Заряд же ядра изменить очень трудно. А если он изменится, то получится уже другой химический элемент.

Так как заряд ядра равен по абсолютному значению общему заряду электронов атома, можно предположить, что в составе ядра находятся положительно заряженные частицы. Их назвали протонами. Масса протона 1,67•10-27 кг, что почти в 1840 раз больше, чем масса электрона.

Заряд протона положителен и равен по абсолютному значению заряду электрона.

Дальнейшее изучение состава ядра позволило предположить, что, кроме протонов, в ядрах атомов содержатся ещё нейтральные (не имеющие заряда) частицы. Они получили название нейтронов. Масса нейтрона не намного больше массы протона.

Итак, строение атома таково: в центре атома находится ядро, состоящее из протонов и нейтронов, а вокруг ядра движутся электроны.

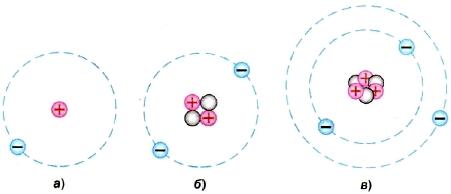
Рис. 40. Модели атомов:
а — водорода; б — гелия; в — лития

На рисунке 40 показаны модели атомов водорода (рис. 40, а), гелия (рис. 40, б) и лития (рис. 40, в). Протоны обозначены на рисунке кружками со знаком « + », нейтроны — серыми кружками (соотношение размеров и расстояний на рисунке не соблюдено).

Напомним, что атом в целом не имеет заряда, он нейтрален, потому что положительный заряд его ядра равен отрицательному заряду всех его электронов.

Но атом, потерявший один или несколько электронов, уже не является нейтральным, а будет иметь положительный заряд. Его называют тогда положительным ионом.

Наблюдается и обратное. Лишний электрон присоединяется к нейтральному атому. В этом случае атом приобретает отрицательный заряд и становится отрицательным ионом.

Вопросы

1. Чем отличаются друг от друга атомы различных химических элементов?
2. Что является главной характеристикой данного химического элемента?
3. Какие частицы входят в состав ядра?
4. Каково строение атомов водорода, гелия и лития?
5. Как образуются положительные и отрицательные ионы?

Упражнение 20

1. В ядре атома углерода содержится 12 частиц. Вокруг ядра движутся 6 электронов. Сколько в ядре этого атома протонов и сколько нейтронов?
2. От атома гелия отделился один электрон. Как называется оставшаяся частица? Каков её заряд?
3. Существуют ли атомы с зарядом ядра меньшим, чем заряд протона?

Вариационный метод

Для большей точности в вычислении энергии удобен вариационный принцип для учёта электрон-электронного взаимодействия V_ee  при использовании волновой функции

ψ(r→1,r→2)=8πa3e−2(r1+r2)a{\displaystyle \psi _{0}({\vec {r}}_{1},\,{\vec {r}}_{2})={\frac {8}{\pi a^{3}}}e^{-2(r_{1}+r_{2})/a}}:

⟨H⟩=8E1+⟨Vee⟩=8E1+(e24πϵ)(8πa3)2∫e−4(r1+r2)a|r1→−r2→|d3r→1d3r→2{\displaystyle \langle H\rangle =8E_{1}+\langle V_{ee}\rangle =8E_{1}+{\Bigg (}{\frac {e^{2}}{4\pi \epsilon _{0}}}{\Bigg )}{\Bigg (}{\frac {8}{\pi a^{3}}}{\Bigg )}^{2}\int {\frac {e^{-4(r_{1}+r_{2})/a}}{|{\vec {r_{1}}}-{\vec {r_{2}}}|}}\,d^{3}{\vec {r}}_{1}\,d^{3}{\vec {r}}_{2}}

После интегрирования получим:

⟨H⟩=8E1+54a(e24πϵ)=8E1−52E1=−109+34=−75 eV{\displaystyle \langle H\rangle =8E_{1}+{\frac {5}{4a}}{\Bigg (}{\frac {e^{2}}{4\pi \epsilon _{0}}}{\Bigg )}=8E_{1}-{\frac {5}{2}}E_{1}=-109+34=-75{\text{ eV}}}

Это значение ближе к экспериментальному значению, но если использовать лучшую пробную функцию то приближение можно улучшить. Идельная пробная функци будет учитывать влияние второго электрона. Другими словами, каждый электрон представляет собой облако отрицательного заряда, которое частично экранирует заряд ядра и, таким образом, электрон движется в эффективном потенциале с зарядом ядра Z, который меньше двух

Принимая во внимание это наблюдение волновая функция запишется в виде:

ψ(r→1,r→2)=Z3πa3e−Z(r1+r2)a{\displaystyle \psi ({\vec {r}}_{1},{\vec {r}}_{2})={\frac {Z^{3}}{\pi a^{3}}}e^{-Z(r_{1}+r_{2})/a}}

Используя Z как вариационный параметр дляя минимизации H. Гамильтониан для этой функции задаётся в виде:

⟨H⟩=2Z2E1+2(Z−2)(e24πϵ)⟨1r⟩+⟨Vee⟩{\displaystyle \langle H\rangle =2Z^{2}E_{1}+2(Z-2){\Bigg (}{\frac {e^{2}}{4\pi \epsilon _{0}}}{\Bigg )}\langle {\frac {1}{r}}\rangle +\langle V_{ee}\rangle }

Вычисляя средние от 1r{\displaystyle {\frac {1}{r}}} и V_ee гамильтониан приводится к виду:

⟨H⟩=−2Z2+274ZE1{\displaystyle \langle H\rangle =E_{1}}

Минимизируя среднюю энергию по Z находим:

ddZ(−2Z2+274ZE1)={\displaystyle {\frac {d}{dZ}}{\Bigg (}E_{1}{\Bigg )}=0}

Z=2716∼1.69{\displaystyle Z={\frac {27}{16}}\sim 1.69}

Это показывает, что второй электрон частично экранирует заряд ядра уменьшая его с 2 до 1,69. В этом случае результат более точный 

12(32)6E1=−77.5 eV{\displaystyle {\frac {1}{2}}{\Bigg (}{\frac {3}{2}}{\Bigg )}^{6}E_{1}=-77.5{\text{ eV}}}

Где, E₁ представляет ионизационную энергию для атома водорода.

Можно использовать следующую формула для лучшего согласия с экспериментом

−4917⋅(1+α)=−2.903386486 a.u.=−79.005153 eV{\displaystyle -{\frac {49}{17}}\cdot (1+\alpha )=-2.903386486{\text{ a.u.}}=-79.005153{\text{ eV}}}

где α{\displaystyle \alpha } — постоянная тонкой структуры.

Используя более сложные и точные вариационные функции, основное состояние атома гелия вычислимо с большей точностью и приближается к экспериментальному значению −78.95 eV. Вариационный подход использовался для вычислений этой системы с высокой точносью в работах G.W.F. Drake и J.D. Morgan III, Jonathan Baker and Robert Hill используя юазисные функции предложенные Hylleraas или Frankowski-Pekeris

следует заметить что для повышения точности до спектроскопических данных нужно принять во внимание эффекты релятивизма и квантовой электродинамики

Где искать электрон?

Наблюдая поведение электрона были выведены определённые закономерности, они описываются
квантовыми числами, всего их четыре:

• Главное квантовое число
• Орбитальное квантовое число
• Магнитное квантовое число
• Спиновое квантовое число

В результате исследования электронного облака, обнаружили, что в зависимости от уровня энергии,
облако принимает четыре основных формы: шар, гантели и другие две, более сложные.
В порядке возрастания энергии, эти формы называются s-,p-,d- и f-оболочкой.
На каждой из таких оболочек может располагаться 1 (на s), 3 (на p), 5 (на d) и 7 (на f)
орбиталей. Орбитальное квантовое число — это оболочка, на которой находятся
орбитали. Орбитальное квантовое число для s,p,d и f-орбиталей соответственно
принимает значения 0,1,2 или 3.

Магнитное квантовое число m_l

На p-оболочке находится три орбитали, они обозначаются цифрами
от -L, до +L, то есть, для p-оболочки (L=1) существуют орбитали «-1», «0» и «1».
Магнитное квантовое число обозначается буквой m_l.

Внутри оболочки электронам легче
располагаться на разных орбиталях, поэтому первые электроны заполняют по одному на каждую
орбиталь, а затем уже к каждому присоединяется его пара.

Спиновое квантовое число m_s

Спин — это направление вращения электрона вокруг своей оси, направлений два, поэтому спиновое квантовое число
имеет два значения: +1/2 и -1/2. На одном энергетическом подуровне могут находиться два электрона только с
противоположными спинами. Спиновое квантовое число обозначается m_s

Главное квантовое число n

Главное квантовое число — это уровень энергии, на данный момент известны семь энергетических уровней,
каждый обозначается арабской цифрой: 1,2,3,…7. Количество оболочек на каждом уровне равно номеру уровня:
на первом уровне одна оболочка, на втором две и т.д.

Сверхтекучесть в иных системах

• Построена сверхтекучая модель атомного ядра, которая достаточно хорошо описывает экспериментальные данные.
• В 1995 году в экспериментах с разрежёнными газами щелочных металлов были достигнуты достаточно низкие температуры для того, чтобы газ перешёл в состояние бозе-эйнштейновского конденсата. Как и ожидалось на основании теоретических вычислений, полученный конденсат вёл себя как сверхтекучая жидкость. В последующих экспериментах было установлено, что при движении тел сквозь этот конденсат со скоростями меньше критической никакой передачи энергии от тела к конденсату не происходит.
• В 2000 году Ян Петер Тоэнниэс демонстрирует сверхтекучесть водорода при 0,15 K
• В 2004 году было объявлено об открытии сверхтекучести и у твёрдого гелия. Последующие исследования, однако, показали, что ситуация далеко не столь проста, и потому говорить об экспериментальном обнаружении этого явления пока преждевременно.
• С 2004 года, на основании результатов ряда теоретических работ предполагается, что при давлениях порядка 4 миллионов атмосфер и выше водород становится неспособным переходить в твёрдую фазу при любом охлаждении (как и гелий при нормальном давлении) образуя тем самым сверхтекучую жидкость. Прямые экспериментальные подтверждения или опровержения пока отсутствуют.
• Существуют также работы, предсказывающие сверхтекучесть в холодном нейтронном или кварковом агрегатном состоянии. Это может оказаться важным для понимания физики нейтронных и кварковых звёзд.
• В 2005 году была открыта сверхтекучесть в холодном разрежённом газе фермионов.
• В 2009 году была продемонстрирована сверхтекучесть типа «supersolid» в холодном разрежённом газе рубидия.

История открытия

Почтовая марка России 2000 года

Сверхтекучесть жидкого гелия-II ниже лямбда-точки (T = 2,172 К) была экспериментально открыта в 1938 году П. Л. Капицей (Нобелевская премия по физике за 1978 год) и Джоном Алленом. Уже до этого было известно, что при прохождении этой точки жидкий гелий испытывает фазовый переход, переходя из полностью «нормального» состояния (называемого гелий-I) в новое состояние так называемого гелия-II, однако только Капица показал, что гелий-II течёт вообще (в пределах экспериментальных погрешностей) без трения.

Теория явления сверхтекучего гелия-II была разработана Л. Д. Ландау (Нобелевская премия по физике за 1962 год).

Гамма-распад

Гамма-распад – это излучение гамма-квантов ядрами в возбужденном состоянии, при котором они обладают большой по сравнению с невозбужденным состоянием энергией. В возбужденное состояние ядра могут приходить при ядерных реакциях либо при радиоактивных

распадах других ядер. Большинство возбужденных состояний ядер имеют очень непродолжительное время жизни – менее наносекунды.

Существуют распады с эмиссией нейтрона, протона, кластерная радиоактивность и некоторые другие, очень редкие виды распадов. Но превалирующие виды радиоактивности это альфа, бета и гамма распад.

Таблица распадов

История изучения радиоактивного излучения. Э. Резерфорд обнаружил две составляющие этого излучения: менее проникающую, названную α-излучением, и более проникающую, названную —излучением.
Третья составляющая урановой радиации, самая проникающая из всех, была
открыта позже, в 1900 году, Полем Виллардом и названа по аналогии с
резерфордовским рядом γ-излучением. Резерфорд и его сотрудники показали,
что радиоактивность связана с распадом атомов (значительно позже стало
ясно, что речь идет о распаде атомных ядер), сопровождающимся выбросом
из них определенного типа излучений. Этот вывод нанес сокрушительный
удар по господствовавшей в физике и химии концепции неделимости атомов.     В последующих исследованиях Резерфорда было показано, что α-излучение представляет собой поток α-частиц, которые являются не чем иным, как ядрами изотопа гелия 4Не, а 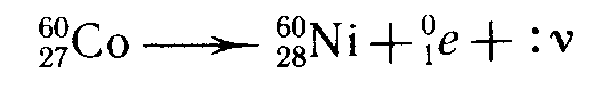β-излучение состоит из электронов и γ-излучение является потоком высокочастотных электромагнитных квантов, испускаемых атомными ядрами при переходе из возбужденных в более низколежащие состояния.     β-распада ядер.
Теория этого явления была создана лишь в 1933 году Энрико Ферми,
который использовал гипотезу Вольфганга Паули о рождении в β-распаде
нейтральной частицы, имеющей близкую к нулю массу покоя и названной
нейтрино .
Ферми обнаружил, что β-распад обусловлен новым типом взаимодействия
частиц в природе — «слабым» взаимодействием и связан с процессами
превращения в родительском ядре нейтрона в протон с испусканием
электрона е- и антинейтрино (β—распад), протона в нейтрон с испусканием позитрона е+ и нейтрино ν (β+-распад), а также с захватом протоном атомного электрона и испусканием нейтрино ν (электронный захват).     Четвертый вид радиоактивности, открытый в России в 1940 году молодыми физиками Г.Н. Флеровым и К.А. Петржаком,
связан со спонтанным делением ядер, в процессе которого некоторые
достаточно тяжелые ядра распадаются на два осколка с примерно равными
массами.     Но и деление не исчерпало всех видов радиоактивных
превращений атомных ядер. Начиная с 50-х годов физики методично
приближались к открытию протонной радиоактивности ядер. Для того чтобы
ядро, находящееся в основном состоянии, могло самопроизвольно испускать
протон, необходимо, чтобы энергия отделения протона от ядра была
положительной. Но таких ядер в земных условиях не существует, и их
необходимо было создать искусственно. К получению таких ядер были очень
близки российские физики в Дубне, но протонную радиоактивность открыли в
1982 году немецкие физики в Дармштадте, использовавшие самый мощный в
мире ускоритель многозарядных ионов. 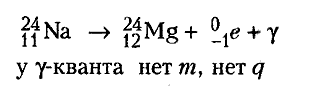    Наконец, в 1984 году
независимые группы ученых в Англии и России открыли кластерную
радиоактивность некоторых тяжелых ядер, самопроизвольно испускающих
кластеры — атомные ядра с атомным весом от 14 до 34.

Закон радиоактивного распада

Если имеется большое количество одинаковых радиоактивных ядер, то вероятность распада каждого из них в любой момент времени одинакова. Радиоактивный распад любого ядра является случайным процессом, поэтому момент его распада предсказать невозможно.

Однако для большого числа частиц, находящихся в образце вещества, выполняется статистический закон радиоактивного распада.

Закон радиоактивного распада: число нераспавшихся атомных ядер при естественном радиоактивном распаде экспоненциально уменьшается с течением времени.

Период полураспада – это время, в течение которого распадается половина способных к распаду ядер.

В начальный момент времени ​\( t \)​ = 0, число атомных ядер ​\( N_0 \)​.

Через промежуток времени, равный периоду полураспада ​\( t=T_{1/2} \)​, число атомных ядер ​\( N=\frac{N_0}{2} \)​.

Через промежуток времени, равный двум периодам полураспада \( t=2T_{1/2} \), число атомных ядер \( N=\frac{N_0}{4}=\frac{N_0}{2^2} \).

Через промежуток времени, равный ​\( n \)​ периодам полураспада ​\( t=nT_{1/2} \)​, число атомных ядер \( N=\frac{N_0}{2^n} \).

где ​\( N \)​ – число нераспавшихся атомных ядер к моменту времени ​\( t \)​; ​\( N_0 \)​ – начальное число атомных ядер; ​\( T_{1/2} \)​ – период полураспада.

На рисунке период полураспада соответствует времени, в течение которого число радиоактивных ядер (активность) уменьшается вдвое.

Детектирование

Детектируются альфа-частицы с помощью сцинтилляционных детекторов, газоразрядных детекторов, кремниевых pin-диодов (поверхностно-барьерных детекторов, нечувствительных к бета- и гамма-излучению) и соответствующей усилительной электроники, а также с помощью трековых детекторов. Для детектирования альфа-частиц с энергиями, характерными для радиоактивного распада, необходимо обеспечить малую поверхностную плотность экрана, отделяющего чувствительный объём детектора от окружающей среды. Например, в газоразрядных детекторах может устанавливаться слюдяное окно с толщиной в несколько микрон, проницаемое для альфа-частиц. В полупроводниковых поверхностно-барьерных детекторах такой экран не нужен, рабочая область детектора может непосредственно контактировать с воздухом. При детектировании альфа-активных радионуклидов в жидкостях исследуемое вещество смешивается с жидким сцинтиллятором.

В настоящее время наиболее распространены кремниевые поверхностно-барьерные детекторы альфа-частиц, в которых на поверхности полупроводникового кристалла с проводимостью p-типа создаётся тонкий слой с проводимостью n-типа путём диффузионного введения донорной примеси (например, фосфора). Приложение обратного смещения к p-n-переходу обедняет чувствительную область детектора носителями заряда. Попадание в эту область альфа-частицы, ионизирующей вещество, вызывает рождение нескольких миллионов электронно-дырочных пар, которые вызывают регистрируемый импульс тока с амплитудой, пропорциональной количеству родившихся пар и, соответственно, кинетической энергии поглощённой альфа-частицы. Поскольку обеднённая область имеет очень малую толщину, детектор чувствителен лишь к частицам с высокой плотностью ионизации (альфа-частицы, протоны, осколки деления, тяжёлые ионы) и малочувствителен к бета- и гамма-излучению.

Энергия связи нуклонов в ядре. Ядерные силы

Между нуклонами ядра действуют самые мощные силы природы – ядерные силы.

Ядерные силы – это силы притяжения, связывающие протоны и нейтроны в атомном ядре и обеспечивающие существование устойчивых ядер.

Свойства ядерных сил:

• являются силами притяжения;
• являются короткодействующими силами (действуют на малых расстояниях, не превышающих 2·10-15 м; на таком расстоянии ядерные силы больше кулоновских приблизительно в 100 раз);
• обладают свойством зарядовой независимости (ядерные силы, действующие между двумя протонами, двумя нейтронами и между протоном и нейтроном, одинаковы);
• имеют свойство насыщения (каждый нуклон взаимодействует только с ограниченным числом ближайших к нему нуклонов, а не со всеми нуклонами ядра);
• не являются центральными (не действуют по линии, соединяющей центры взаимодействующих нуклонов).

Массу ядра можно точно определить с помощью масс-спектрографов, которые разделяют заряженные частицы с разными удельными зарядами с помощью электрических и магнитных полей.

Опытным путем было установлено, что благодаря действию сил притяжения масса ядра всегда меньше суммы масс протонов и масс нейтронов, входящих в состав этого ядра:

где ​\( M \)​ – масса ядра.

Дефект масс – это величина, равная разности суммы масс входящих в ядро нуклонов и массы ядра:

где ​\( \Delta m \)​ – дефект масс.

Благодаря ядерным силам ядра атомов обладают огромной энергией связи.

Энергия связи – это энергия, которую необходимо затратить, чтобы разделить ядро на составляющие его нуклоны, или энергия, которая выделяется при образовании ядра из отдельных нуклонов:

где ​\( \Delta E_{св} \)​ – энергия связи, ​\( c \)​ – скорость света.

Если в формуле энергии связи массы протона и нейтрона выражены в килограммах, а скорость света – в метрах в секунду, то энергия связи будет измерена в джоулях. Однако в физике атома и атомного ядра энергию ядер и элементарных частиц чаще выражают в мегаэлектронвольтах (МэВ).

Энергетический эквивалент 1 а.е.м.

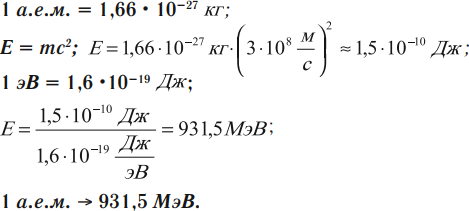
Поэтому энергию связи можно рассчитать следующим образом:

В этом случае энергия связи измеряется в мегаэлектронвольтах (МэВ).

Для характеристики прочности ядра используется величина, которая называется удельной энергией связи.

Удельная энергия связи – это энергия связи ядра, приходящаяся на один нуклон ядра:

где ​\( A \)​ – массовое число.

Удельная энергия связи неодинакова для разных химических элементов и даже для изотопов одного и того же химического элемента. Удельная энергия связи нуклона в ядре меняется в среднем в пределах от 1 МэВ у легких ядер до 8,6 МэВ у ядер средней массы (с массовым числом ​\( A \)​ ≈ 100). У тяжелых ядер (​\( A \)​ ≈ 200) удельная энергия связи нуклона меньше, чем у ядер средней массы, приблизительно на 1 МэВ, так что их превращение в ядра среднего веса (деление на 2 части) сопровождается выделением энергии в количестве около 1 МэВ на нуклон, или около 200 МэВ на ядро. Превращение легких ядер в более тяжелые ядра дает еще больший энергетический выигрыш в расчете на нуклон.

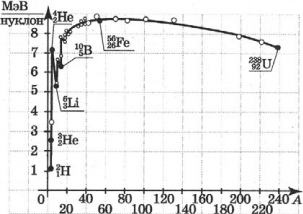
Зависимость удельной энергии связи от массового числа установили экспериментально. Из рисунка хорошо видно, что, не считая самых легких ядер, удельная энергия связи примерно постоянна и равна 8 МэВ/нуклон. Отметим, что энергия связи электрона и ядра в атоме водорода, равная энергии ионизации, почти в миллион раз меньше этого значения. Кривая на рисунке имеет слабо выраженный максимум. Максимальную удельную энергию связи (8,6 МэВ/нуклон) имеют элементы с массовыми числами от 50 до 60, т. е. железо и близкие к нему по порядковому номеру элементы. Ядра этих элементов наиболее устойчивы.

У тяжелых ядер удельная энергия связи уменьшается за счет возрастающей с увеличением ​\( Z \)​ кулоновской энергии отталкивания протонов. Кулоновские силы стремятся разорвать ядро.

Образование

Альфа-частицы возникают при альфа-распаде ядер, при ядерных реакциях и в результате полной ионизации атомов гелия-4. Например, в результате взаимодействия ядра лития-6 с дейтроном могут образоваться две альфа-частицы: 6Li+2H=4He+4He. Альфа-частицы составляют существенную часть первичных космических лучей; большинство из них являются ускоренными ядрами гелия из звёздных атмосфер и межзвёздного газа, некоторые возникли в результате ядерных реакций скалывания из более тяжёлых ядер космических лучей. Альфа-частицы высоких энергий могут быть получены с помощью ускорителей заряженных частиц.

Энергия образования

Чтобы рассчитать энергию образования альфа-частицы, следует воспользоваться знаменитым уравнением Эйнштейна, которое связывает массу и энергию через одну из фундаментальных постоянных нашей Вселенной — скорость света. Это уравнение имеет вид: E = mc2, где E — энергия, m — масса, c — скорость света в вакууме.

Зная, что при образовании альфа-частицы масса ее компонентов уменьшается на 0,015 * 10-27 кг, а также зная, что скорость света составляет 3 * 108 м/с, получаем энергию, которая выделяется во время этого процесса. Она равна E = 0,015 * 10-27 * 9 * 1016 = 1,35 * 10-12 Дж. В физике элементарных частиц принято энергии записывать в электрон-вольтах (эВ). Один электрон-вольт равен 1,602177 * 10−19 Дж. Тогда энергия образования альфа-частицы равна 8,426 * 106 эВ, или 8,426 МэВ (мегаэлектрон-вольт).

Чтобы понять, насколько велика эта энергия, можно провести простой расчет. Представим, что вся энергия образования альфа-частицы переводится на ее ускорение. Пользуясь уравнением Лоренца для нерелятивистских скоростей, то есть полагая, что кинетическая энергия-альфа частицы равна mv2/2, где v — скорость ее движения, получаем, что этой энергии образования будет достаточно, чтобы разогнать альфа-частицу до скорости 2 * 107 м/c, что составляет 6,7 % от скорости света в вакууме. Отметим, что задавать вопрос о том, на сколько увеличится масса альфа-частицы при таких скоростях, не имеет смысла, поскольку увеличением ее массы можно пренебречь, так как она составит всего 0,015/6,68 * 100 = 0,2 %.