Электродинамика (объяснение явлений; интерпретация результатов опытов)
Содержание:
Проверка практикой
Эта теория может объяснить, как биполяроны могут существовать при комнатных температурах, а также то, почему они возникают в «водородных» сверхпроводниках, которые по своим свойствам и структуре радикально отличаются от купратов и других металлических материалов такого рода.
«Теория – это одно дело, однако в дальнейшее развитие сверхпроводников должен вступить инженерный ум. В данном случае теория позволяет нам двигаться вперед не на ощупь, а осознанно. К примеру, я предложил простой подход: поскольку концентрация пар маленькая, то мы можем увеличить ее, взяв сверхпроводящий кабель и легировав его периферию магнитными примесями. Это приведет к увеличению концентрации пар в его середине», – отметил Лахно.
Как предполагает физик, эту идею можно достаточно легко воплотить на практике, если бы ей заинтересовался один из производителей высокотемпературных сверхпроводников. Проверить его гипотезу иначе можно в экспериментах, которые могли бы показать, что пары биполяронов будут существовать при высоких температурах.
По словам Лахно, подобные опыты в прошлом году уже провели физики из Йельского университета. Их эксперименты указали на то, что внутри медных высокотемпературных сверхпроводников есть определенные пары частиц, которые не распадаются при высоких температурах. Как предполагает ученый, они представляют собой пары биполяронов из его теории.
«Если мы подтвердим, что эти частицы существуют в конденсированной материи, то перед нами откроются чрезвычайно широкие теоретические перспективы и в других областях, в том числе в космологии и атомной физике. Нам, однако, нужно в первую очередь решать земные вопросы и создать реальные высокотемпературные сверхпроводники. До эпидемии я думал, что первые сверхпроводники, работающие при комнатной температуре и высоком давлении, появятся уже в этом году, однако теперь этот прогноз надо сдвинуть на полгода-год. А полностью эта задача будет решена в ближайшие одно-два десятилетия», – подытожил физик.
§ 3. Электродинамика
3.1. Основные понятия и законы электростатики
Закон Кулона:

 ε = 8, 85 · 10−12 Ф/мТочечными зарядамиНапряжённость электрического поля
ε = 8, 85 · 10−12 Ф/мТочечными зарядамиНапряжённость электрического поля Работа электрического поля
Работа электрического поля
 Потенциалом электрического поля
Потенциалом электрического поля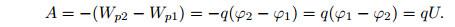 U = ϕ1 − ϕ2разность потенциаловнапряжениемПотенциал поля точечного заряда
U = ϕ1 − ϕ2разность потенциаловнапряжениемПотенциал поля точечного заряда
3.3. Основные понятия и законы постоянного тока
Электрический токЗакон Ома для участка цепиэлектрическим сопротивлениемСопротивление проводника
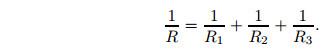 электродвижущей силойзаконом Ома для полной цепи
электродвижущей силойзаконом Ома для полной цепи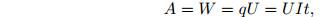 Закон Джоуля-Ленца:
Закон Джоуля-Ленца:
3.4. Основные понятия и законы магнитостатики
магнитная индукция ➛B.правила буравчика:Магнитным потоком Φ сила АмпераЗакон Ампера:
сила АмпераЗакон Ампера: левой
левой
руки:сила Лоренца. правила левой руки
правила левой руки
Варианты физических олимпиад
Всероссийская олимпиада школьников по физике
На пересечении строки (ваш класс) и столбца (этап Всеросса) находятся ссылки на варианты. Цифры ссылки — год проведения финала олимпиады.
| ШЭ | МЭ | РЭ | ЗЭ | |
|---|---|---|---|---|
| 7 класс |
, , , , , , |
, , , , , |
, | — |
| 8 класс |
, , , , , , |
, , , , , |
, , |
— |
| 9 класс |
, , , , , |
, , , , |
, , , , , , , , , , , , , , , , , , , , , , |
, , , , , , , , , , , , , , , , , , , , , , |
| 10 класс |
, , , , , |
, , , , |
, , , , , , , , , , , , , , , , , , , , , , |
, , , , , , , , , , , , , , , , , , , , , , |
| 11 класс |
, , , , , |
, , , , |
, , , , , , , , , , , , , , , , , , , , , , |
, , , , , , , , , , , , , , , , , , , , , , |
На основе классификации задач 1992–2017 годов составлены программы подготовки к региональному и заключительному этапам:
- 9 класс;
- 10 класс.
Московская олимпиада школьников по физике
| Нулевой тур | Первый тур | Второй тур | |
|---|---|---|---|
| 7 класс |
19.0, 19.118.0, 18.117.0, 17.116.0, 16.115.0, 15.114.0, 14.1, 14.2, 14.3, 14.4 |
, , , , , , , , , , |
, , , |
| 8 класс |
19.0, 19.118.0, 18.117.0, 17.116.0, 16.115.0, 15.114.0, 14.1, 14.2, 14.3, 14.4 |
, , , , , , , , , , |
, , , , , , , , , , |
| 9 класс |
19.0, 19.118.0, 18.117.0, 17.116.0, 16.115.0, 15.114.0, 14.1, 14.2, 14.3, 14.4 |
, , , , , , , , , , |
, , , , , , , , , , |
| 10 класс |
19.0, 19.118.0, 18.117.0, 17.116.0, 16.115.0, 15.114.0, 14.1, 14.2, 14.3, 14.4 |
, , , , , , , , , , |
, , , , , , , , , , |
| 11 класс |
19.0, 19.1, 19.2, 19.T18.0, 18.1, 18.2, 18.317.0, 17.1, 17.2, 17.316.0, 16.1, 16.2, 16.315.0, 15.1, 15.2, 15.314.0, 14.1, 14.2, 14.3, 14.4 |
, , , , , , , , , , |
, , , , , , , , , , |
Примечания.
- Для 7–10 классов финалом является второй тур (победители и призёры определяются по количеству баллов на втором туре). Нулевой и первый туры служат отборочным этапом.
- Для 11 класса финалом являются первый и второй туры (победители и призёры определяются по сумме баллов на первом и втором турах). Нулевой тур служит отборочным этапом; поэтому число заочных заданий нулевого тура в 11 классе больше, чем в 7–10 классах.
- Второй тур для 7 класса впервые проведён в 2015 году. До 2014 года включительно финалом в 7 классе был первый тур.
- Нулевой тур проводится с 2013/14 года. До этого был просто «отборочный этап».
Олимпиада «Физтех»
| Онлайн | Финал | |
|---|---|---|
| 7 класс |
, , , |
— |
| 8 класс |
, , , |
— |
| 9 класс |
, , , , |
20.1, 20.219.1, 19.218.1, 18.217.1, 17.216.1, 16.2, 16.3 |
| 10 класс |
, , , , , |
20.1, 20.219.1, 19.218.1, 18.217.1, 17.216.1, 16.2, 16.315.1, 15.2, 15.3 |
| 11 класс |
, , , , , |
20.1, 20.219.1, 19.218.1, 18.2, 18.3, 18.417.1, 17.216.1, 16.2, 16.315.1, 15.2, 15.314.1, 14.2; 13.1, 13.212.1, 12.2; 11.1, 11.2; 09.1, 09.2; , |
Примечания.
- Очный финал для 7–8 классов пока не проводится.
- Очный финал для 10 класса впервые прошёл в 2015 году, а для 9 класса — в 2016 году.
- В 2016/17 и 2017/18 годах на онлайн-этапе для 7 класса давалось задание 8 класса.
- Задания онлайн-этапа 2012/13 года найти не удалось.
Открытая олимпиада Физтех-лицея 2014/15 года —
7 класс,
8 класс,
9 класс,
10 класс,
11 класс.
Олимпиада «Покори Воробьёвы горы!»
| 7–9 классы |
19.1, 19.2, 19.3, 19.4, 19.518.1, 18.2, 18.317.1, 17.2, 17.316.1, 16.2; , |
| 10–11 классы |
19.1, 19.2, 19.3, 19.4, 19.5, 19.618.1, 18.2, 18.3, 18.417.1, 17.2, 17.3, 17.4, 17.5, 17.616.1, 16.2, 16.3, 16.4, 16.5, 16.6, 16.715.1, 15.2, 15.3, 15.5, 15.7, 15.8, 15.914.1, 14.2, 14.3, 14.4, 14.5, 14.6, 14.7 |
Олимпиада «Росатом»
| 7 класс |
, , , , , , , , |
| 8 класс |
20.1, 20.2, , 17.1, 17.2, , , , , |
| 9 класс |
20.1, 20.2, 20.3, , 17.1, 17.2, , , , , |
| 10 класс |
20.1, 20.2, 20.3, , 17.1, 17.2, , , , , |
| 11 класс |
20.1, 20.2, 20.319.1, 19.2, 19.318.1, 18.2, 18.3, 18.417.1, 17.2, 17.3, 17.4, , 13.1, 13.2, 13.3, 13.4, 13.5, 13.612.1, 12.2, 12.3, 12.4, 12.511.1, 11.2, 11.3, 11.4, 11.5 11.6 |
Теория к заданию 23 из ЕГЭ по физике
6.1. Основные понятия и законы квантовой физики
Фотоэффектом называется потеря телами электронов под действием света. Существует критическая длина волны (своя для каждого металла), с превышением которой фотоэффект прекращается. Т.к. эта длина волны лежит в длинноволновой области спектра, то её принято называть красной границей фотоэффекта
Для фотоэффекта Эйнштейн привлёк представление о фотонах (квантах света), предложенное Планком для объяснения теплового излучения тел. Уравнение Эйнштейна для фотоэффекта имеет вид: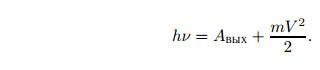
Постулаты Бора:
1) электроны движутся в атоме по стационарным орбитам, на которых они обладают энергией, но энергии не излучают
Таких стационарных орбит в атоме несколько. Нижняя орбита называется основным состоянием атома, остальные — возбуждённым состоянием атома;
2) переходя с одной стационарной орбиты на другую, электрон испускает или поглощает квант электромагнитной энергии, чья энергия пропорциональна частоте:
6.2. Основные понятия и законы ядерной физики
В 1932 г. советский физик Иваненко и немецкий физик Гейзенберг предложили протонно-нейтронную модель ядра атома. По этой модели ядро атома состоит из двух видов элементарных частиц — протонов и нейтронов. Так как в целом атом электрически нейтрален, то число протонов в ядре равно числу электронов в атомной оболочке. Следовательно, число протонов равно атомному номеру элемента (Z) таблицы Менделеева. Сумму числа протонов Z и числа нейтронов N называют массовым числом и обозначают A.
Под энергией связи понимают ту энергию, которая необходима для полного расщепления ядра на отдельные нуклоны. Энергию связи атомных ядер можно рассчитать по формуле
Величину ∆M называют дефектом масс, который определяется по формуле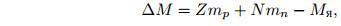
где mp — масса протона, mn — масса нейтрона.
Самопроизвольное испускание неких частиц атомами получило название радиоактивность. Было установлено, что радиоактивные элементы испускают три вида излучения. Их назвали α-, β- и γ- лучами.
Природа α-, β- и γ- лучей различна. γ-лучи — это электромагнитные волны с очень маленькой длиной волны (от 10−8 до 10−11 см). β-лучи — это электроны, движущиеся со скоростями, близкими к скорости света. α-лучи — это поток ядер атомов гелия (дважды ионизированные атомы гелия). α-, β- и γ- лучи испускаются атомами радиоактивных элементов при их превращениях.
Для α- и β-распада действует правило смещения: при α-распаде ядро теряет положительный заряд 2e, а масса его убывает на 4 атомных единицы. В результате элемент смещается на 2 клетки к началу периодической системы. Если α-распад претерпевает элемент X, то в результате получается элемент Y :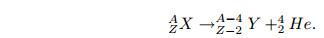
При β-распаде из ядра вылетает электрон. Он символически изображается -1e, т. к. масса его очень мала. После β-распада элемент смещается на одну клетку к концу таблицы Менделеева: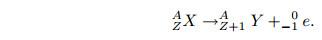
При γ-распаде заряд не меняется, масса ядра меняется ничтожно мало.
Число α-распадов
Число β-распадов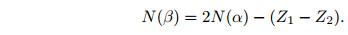
Основные теоретические сведения
Импульс тела
Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р. Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:
Направление вектора импульса совпадает с направлением вектора скорости тела (направлен по касательной к траектории). Единица измерения импульса – кг∙м/с.
Изменение импульса одного тела находится по формуле (обратите внимание, что разность конечного и начального импульсов векторная):
где: pн – импульс тела в начальный момент времени, pк – в конечный. Главное не путать два последних понятия.
Абсолютно упругий удар – абстрактная модель соударения, при которой не учитываются потери энергии на трение, деформацию, и т.п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется. Может поменяться только его направление. При этом угол падения равен углу отражения.
Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Например, пластилиновый шарик при падении на любую поверхность полностью прекращает свое движение, при столкновении двух вагонов срабатывает автосцепка и они так же продолжают двигаться дальше вместе.
Закон сохранения импульса
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения импульса (ЗСИ). Следствием его являются законы Ньютона. Второй закон Ньютона в импульсной форме может быть записан следующим образом:
Как следует из данной формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Аналогично можно рассуждать для равенства нулю проекции силы на выбранную ось. Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Аналогичные записи можно составить и для остальных координатных осей. Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.
Сохранение проекции импульса
Возможны ситуации, когда закон сохранения импульса выполняется только частично, то есть только при проектировании на одну ось. Если на тело действует сила, то его импульс не сохраняется. Но всегда можно выбрать ось так, чтобы проекция силы на эту ось равнялась нулю. Тогда проекция импульса на эту ось будет сохраняться. Как правило, эта ось выбирается вдоль поверхности по которой движется тело.
Многомерный случай ЗСИ. Векторный метод
В случаях если тела движутся не вдоль одной прямой, то в общем случае, для того чтобы применить закон сохранения импульса, нужно расписать его по всем координатным осям, участвующим в задаче. Но решение подобной задачи можно сильно упростить, если использовать векторный метод. Он применяется если одно из тел покоится до или после удара. Тогда закон сохранения импульса записывается одним из следующих способов:
Из правил сложения векторов следует, что три вектора в этих формулах должны образовывать треугольник. Для треугольников применяется теорема косинусов.
Проблемы теории
«У теории БКШ и других объяснений существованию сверхпроводников есть и другие проблемы. К примеру, долгое время ученые считали, что в формировании куперовских пар участвуют все свободные электроны. На самом деле это не так. В 2016 году наши коллеги из США провели серию экспериментов, которая показала, что лишь небольшая часть частиц участвовала в их образовании», – пояснил ученый.
Как отметил Лахно, его теория разрешает эту проблему, а также объясняет многие другие необычные особенности, характерные как для купратов, давно известных высокотемпературных сверхпроводников на основе меди, так и для недавно открытых веществ подобного рода. В их число входят различные соединения водорода и некоторых других элементов, в том числе серы, лантана, актиния.
По его мнению, необычные свойства новых сверхпроводников, а также все характерные черты их классических аналогов могут объясняться тем, что сверхпроводящие материалы по структуре похожи на своеобразный двумерный или даже одномерный материал с необычными физическими свойствами.
В прошлом ученые считали, что двумерные аналоги конденсата Бозе–Эйнштейна не могут существовать в принципе. Однако несколько лет назад российские физики-теоретики, в том числе Лахно, показали, что подобные структуры могут существовать внутри особых структур и зон в высокотемпературных сверхпроводниках.
«Биполяроны в сверхпроводниках обладают крайне необычными свойствами, они ведут себя как волны, а не как частицы, которые можно локализовать в конкретных точках пространства. Они образуют конденсат Бозе – Эйнштейна, их уже давно пытались связать со сверхпроводимостью. Однако их существование при высоких температурах раньше считалось невозможным. Наша теория показывает, что это возможно для делокализованных квазичастиц, которые могут двигаться по всему кристаллу и сохраняют стабильность не только при низких температурах», – пояснил Лахно.