Изотопы железа
Содержание:
- Самый дорогой металл
- Примеры расчётов
- Главный поставщик биосферного радионуклида
- Стабильность периода полураспада
- Эфиры тестостерона и его производных[править | править код]
- Гамма-распад (изомерный переход)
- Таблица изотопов железа
- ПримерПравить
- Теория
- Временной интервал в радиоактивности
- Закон радиоактивного распада
Самый дорогой металл
Известно, что в наше время есть металлы значительно более дорогие, чем золото, серебро и платина. К ним относится и плутоний. Интересно, что в природе созданный в процессе эволюции плутоний не встречается. Большинство элементов получены в лабораторных условиях. Эксплуатация плутония-239 в ядерных реакторах дала возможность ему стать чрезвычайно популярным в наши дни. Получение достаточного для использования в реакторах количества данного изотопа делает его практически бесценным.

Плутоний-239 получается в естественных условиях как следствие цепочки превращений урана-239 в нептуний-239 (период полураспада — 56 часов). Аналогичная цепочка позволяет накопить плутоний в ядерных реакторах. Скорость появления необходимого количества превосходит естественную в миллиарды раз.
Примеры расчётов
Пример 1
Если рассматривать достаточно близкие моменты времени t1{\displaystyle t_{1}} и t2{\displaystyle t_{2}}, то число ядер, распавшихся за этот промежуток времени t2−t1≪λ{\displaystyle t_{2}-t_{1}\ll \lambda }, можно приближённо записать как ΔN≈λN(t2−t1){\displaystyle \Delta N\approx \lambda N_{0}(t_{2}-t_{1})}.
С её помощью легко оценить число атомов урана-238, имеющего период полураспада T12=4,498⋅109{\displaystyle T_{1/2}=4,498\cdot 10^{9}} лет, испытывающих превращение в данном количестве урана, например, в одном килограмме в течение одной секунды. Имея в виду, что количество любого элемента в граммах, численно равное атомному весу, содержит, как известно, 6,02⋅1023 атомов, а в году 365⋅24⋅60⋅60{\displaystyle 365\cdot 24\cdot 60\cdot 60} секунд, можно получить, что
- ΔN≈,6934,498⋅109⋅365⋅24⋅60⋅606,02⋅1023238⋅1000=12⋅106.{\displaystyle \Delta N\approx {\frac {0,693}{4,498\cdot 10^{9}\cdot 365\cdot 24\cdot 60\cdot 60}}{\frac {6,02\cdot 10^{23}}{238}}\cdot 1000=12\cdot 10^{6}.}
Вычисления приводят к тому, что в одном килограмме урана в течение одной секунды распадается двенадцать миллионов атомов. Несмотря на такое огромное число, всё же скорость превращения ничтожно мала. Действительно, в секунду из наличного количества урана распадается его доля, равная
- 12⋅106⋅2386,02⋅1023⋅1000=47⋅10−19.{\displaystyle {\frac {12\cdot 10^{6}\cdot 238}{6,02\cdot 10^{23}\cdot 1000}}=47\cdot 10^{-19}.}
Пример 2
Образец содержит 10 г изотопа плутония Pu-239 с периодом полураспада 24 400 лет. Сколько атомов плутония распадается ежесекундно?
Поскольку рассматриваемое время (1 с) намного меньше периода полураспада, можно применить ту же, что и в предыдущем примере, приближённую формулу:
- ΔN≈Δt⋅Nln2T12=Δt⋅mμNAln2T12{\displaystyle \Delta N\approx \Delta t\cdot N_{0}{\frac {\ln 2}{T_{1/2}}}=\Delta t\cdot {\frac {{\frac {m}{\mu }}N_{A}\ln 2}{T_{1/2}}}}
Подстановка численных значений даёт
ΔN≈1⋅,693⋅10239⋅6⋅102324400⋅365⋅24⋅60⋅60=,693⋅2,5⋅10227,7⋅1011=2,25⋅1010.{\displaystyle \Delta N\approx 1\cdot {\frac {0,693\cdot {\frac {10}{239}}\cdot 6\cdot 10^{23}}{24400\cdot 365\cdot 24\cdot 60\cdot 60}}={\frac {0,693\cdot 2,5\cdot 10^{22}}{7,7\cdot 10^{11}}}=2,25\cdot 10^{10}.}
Когда рассматриваемый период времени сравним с периодом полураспада, следует пользоваться точной формулой
- ΔN=N−N(t)=N(1−2−tT12).{\displaystyle \Delta N=N_{0}-N(t)=N_{0}\left(1-2^{-t/T_{1/2}}\right).}
Она пригодна в любом случае, однако для малых периодов времени требует вычислений с очень большой точностью. Так, для данной задачи:
- ΔN=N(1−2−tT12)=2.5⋅1022(1−2−17.7⋅1011)=2.5⋅1022(1−0.99999999999910)=2.25⋅1010.{\displaystyle \Delta N=N_{0}\left(1-2^{-t/T_{1/2}}\right)=2.5\cdot 10^{22}\left(1-2^{-1/7.7\cdot 10^{11}}\right)=2.5\cdot 10^{22}\left(1-0.99999999999910\right)=2.25\cdot 10^{10}.}
Главный поставщик биосферного радионуклида
Источником биосферного радиоактивного нуклида цезия-137 с периодом полураспада больше 30 лет является ядерная энергетика.
Статистика неумолима. По данным 2000 года, всеми реакторами атомных электростанций мира в атмосферу выброшено порядка около 22,2 × 1019 Бк цезия-137, период полураспада которого — более 30 лет.
Загрязняется не только атмосфера. С танкеров и ледоколов с атомными установками, с подводных атомных лодок в год в океан попадает данный радионуклид. Так, по подсчетам специалистов, в течение работы одного реактора подводной лодки в течение одного года в океан попадет порядка 24 х 1014 Бк. Если учесть время полураспада цезия-137, это становится опасным источником очень длительного загрязнения окружающей среды.
Стабильность периода полураспада
Во всех наблюдавшихся случаях (кроме некоторых изотопов, распадающихся путём электронного захвата) период полураспада был постоянным (отдельные сообщения об изменении периода были вызваны недостаточной точностью эксперимента, в частности, неполной очисткой от высокоактивных изотопов). В связи с этим период полураспада считается неизменным. На этом основании строится определение абсолютного геологического возраста горных пород, а также радиоуглеродный метод определения возраста биологических останков: зная концентрацию радиоизотопа в настоящее время и в прошлом, можно рассчитать, сколько точно времени прошло с тех пор.
Предположение об изменяемости периода полураспада используется креационистами, а также представителями т. н. «альтернативной науки» для опровержения научной датировки горных пород, остатков живых существ и исторических находок, с целью дальнейшего опровержения научных теорий, построенных с использованием такой датировки. (См., например, статьи Креационизм, Научный креационизм, Критика эволюционизма, Туринская плащаница).
Вариабельность постоянной распада для электронного захвата наблюдалась в эксперименте, но она лежит в пределах процента во всём доступном в лаборатории диапазоне давлений и температур. Период полураспада в этом случае изменяется в связи с некоторой (довольно слабой) зависимостью плотности волновой функции орбитальных электронов в окрестности ядра от давления и температуры. Существенные изменения постоянной распада наблюдались также для сильно ионизованных атомов (так, в предельном случае полностью ионизованного ядра электронный захват может происходить только при взаимодействии ядра со свободными электронами плазмы; кроме того, распад, разрешённый для нейтральных атомов, в некоторых случаях для сильно ионизованных атомов может быть запрещён кинематически). Все эти варианты изменения постоянных распада, очевидно, не могут быть привлечены для «опровержения» радиохронологических датировок, поскольку погрешность самого радиохронометрического метода для большинства изотопов-хронометров составляет более процента, а высокоионизованные атомы в природных объектах на Земле не могут существовать сколько-нибудь длительное время.
Поиск возможных вариаций периодов полураспада радиоактивных изотопов, как в настоящее время, так и в течение миллиардов лет, интересен в связи с гипотезой о вариациях значений фундаментальных констант в физике (постоянной тонкой структуры, константы Ферми и т. д.). Однако тщательные измерения пока не принесли результата — в пределах погрешности эксперимента изменения периодов полураспада не были найдены. Так, было показано, что за 4,6 млрд лет константа α-распада самария-147 изменилась не более чем на 0,75 %, а для β-распада рения-187 изменение за это же время не превышает 0,5 %; в обоих случаях результаты совместимы с отсутствием таких изменений вообще.
Эфиры тестостерона и его производных[править | править код]
Строение эфиров и время полувыведения (из «Анаболик Ревю»)
Время полувыведения инъекционных стероидов с указанием источников
Эфир — это остаток карбоновой кислоты, присоединяемый к спиртовой группе молекулы анаболического стероида, с целью придания ему необходимых фармакологических свойств: депонирование и медленное высвобождение в кровь.
Большинство анаболических стероидов очень быстро разрушаются в организме, например, введение чистого тестостерона требует выполнения ежедневных уколов. Для удобства были изобретены депо-препараты, которые представляют собой комплекс «анаболик+эфир», растворенный в масле. Эфиры хорошо растворимы в масле и плохо в воде, однако если масляный раствор капнуть в воду, то молекулы «анаболик+эфир» будут очень медленно переходить из масла в воду.
В месте инъекции (чаще внутри мышцы) образуется масляное депо, из которого происходит выделение препарата в кровоток. Скорость перехода стероида в кровь характеризуется периодом полужизни его эфира. Период полужизни (или полураспада или полувыведения) — это время, за которое концентрация эфира в крови после 1 инъекции снизится ровно на 50% (половина препарата выведется из организма). Существует множество различных эфиров, различающихся между собой только периодом полураспада.
- Более длинные эфиры лучше растворяются в масле, за счет высокой липофильности, медленнее поступают в кровоток, и имеют более продолжительный период полураспада.
- Продолжительность действия равна примерно двум периодам полувыведения. Таким образом, чем длиннее цепочка эфира, тем больше продолжительность действия препарата.
Никакого влияния на свойства стероида, кроме продолжительности действия, эфиры не оказывают.
Виды эфировправить | править код
Рассмотрим наиболее употребляемые эфиры тестостерона и его производных в бодибилдинге.
Ацетат. Имеет наименьший период полураспада, равный примерно 1 суткам. С данным эфиром, наиболее употребляемыми являются такие стероиды как тренболон и примоболан. Кроме того, тестостерона ацетат входит в пятиэфирную смесь эфиров тестостерона набирающей популярность фирмы Lyka Labs.
Пропионат. Один из наиболее известных эфиров, благодаря распространенному приему бодибилдерами тестостерона пропионата. Кроме того, из наиболее частых применений пропионата — дростанолон пропионат (мастерон) и метандриол дипропионат. Имеет период полураспада в диапазоне от одного до двух суток.
Фенилпропионат. На основе данного эфира наиболее известен нандролон фенилпропионат. Выпускается и тестостерона фенилпропионат. Также используется в смесях тестостерона, таких как сустанон, омнадрен и др. Период полураспада 2 — 3 суток.
Изокапроат (изогексаноат). Входит в состав сустанона и омнадрена наряду с другими эфирами тестостерона. Период полураспада равен 4 — 5 суток
Энантат. Один из наиболее часто используемых эфиров. Используется с тестостероном, тренболоном, метенолоном и другими препаратами. Имеет период полураспада 5-7 суток.
Гексагидробензилкарбонат или циклогексилметилкарбонат (синонимы: гексагидробенциклокарбонат, англ.: cyclohexylmethylcarbonate, hexahydrobencylcarbonic или hexahydrobenzyl carbonate). Цепочка имеет 8 атомов углерода, хотя часто встречается ошибочное указание на 7 атомов, период полужизни по разным источникам примерно 6-8 дней, по свойствам схож с энантатом. Встречается у тренболона (параболан). Наименования отличаются по причине использования различных номенклатур.
Ципионат. Практически взаимозаменяем с энантатом. Наиболее распространен в США, хотя и у нас встречается довольно часто в виде ципионата тестостерона и нандролона. Период полужизни до 7 суток.
Деканоат. Сразу вспоминается деканоат нандролона, хотя также входит в состав сустанона, как эфир с самым большим сроком действия в нем. Период полураспада по разным данным 7 — 9 суток. Для поддержания постоянного уровня в крови, инъекции делаются в среднем раз в неделю. Ранее выпускался как отдельный препарат под маркой Neotest 250 (Loeffler), однако больше не производится.
Ундециленат или ундесиленат. Имеет период полураспада 9 — 11 суток. Из наиболее известных применений — болденона ундециленат.
Лаурат. Период полураспада 10 — 12 суток. Наиболее долгоиграющий эфир из использующихся в бодибилдинге. Из применений — нандролона лаурат.
Существует еще немало эфиров, однако они в бодибилдинге практически не используются или используются довольно редко, поэтому в данную статью не вошли.
Механизм действия всех этих эфиров на организм достаточно хорошо изучен и, кроме времени всасывания стероида в кровоток, ни на какие другие характеристики действия данного стероида влияния не оказывает.
Гамма-распад (изомерный переход)
Основная статья: Изомерия атомных ядер
Почти все ядра имеют, кроме основного квантового состояния, дискретный набор возбуждённых состояний с большей энергией (исключением являются ядра 1H, 2H, 3H и 3He). Возбуждённые состояния могут заселяться при ядерных реакциях либо радиоактивном распаде других ядер. Большинство возбуждённых состояний имеют очень малые времена жизни (менее наносекунды). Однако существуют и достаточно долгоживущие состояния (чьё время жизни измеряется микросекундами, сутками или годами), которые называются изомерными, хотя граница между ними и короткоживущими состояниями весьма условна. Изомерные состояния ядер, как правило, распадаются в основное состояние (иногда через несколько промежуточных состояний). При этом излучаются один или несколько гамма-квантов; возбуждение ядра может сниматься также посредством вылета конверсионных электронов из атомной оболочки. Изомерные состояния могут распадаться также и посредством обычных бета- и альфа-распадов.
Таблица изотопов железа
| Символ нуклида | Z (p) | N (n) | Масса изотопа (а. е. м.) | Период полураспада(T1/2) | Спин и чётность ядра |
|---|---|---|---|---|---|
| Энергия возбуждения | |||||
| 45Fe | 26 | 19 | 45,01458 | 4,9 мс | 3/2+ |
| 46Fe | 26 | 20 | 46,00081 | 9 мс | 0+ |
| 47Fe | 26 | 21 | 46,99289 | 21,8 мс | 7/2- |
| 48Fe | 26 | 22 | 47,98050 | 44 мс | 0+ |
| 49Fe | 26 | 23 | 48,97361 | 70 мс | 7/2- |
| 50Fe | 26 | 24 | 49,96299 | 155 мс | 0+ |
| 51Fe | 26 | 25 | 50,956820 | 305 мс | 5/2- |
| 52Fe | 26 | 26 | 51,948114 | 8,275 ч | 0+ |
| 52mFe | 6,81 МэВ | 45,9 с | 12+ | ||
| 53Fe | 26 | 27 | 52,9453079 | 8,51 мин | 7/2- |
| 53mFe | 3,040 МэВ | 2,526 мин | 19/2- | ||
| 54Fe | 26 | 28 | 53,9396105 | стабилен | 0+ |
| 54mFe | 6,5269 МэВ | 364 нс | 10+ | ||
| 55Fe | 26 | 29 | 54,9382934 | 2,737 лет | 3/2- |
| 56Fe | 26 | 30 | 55,9349375 | стабилен | 0+ |
| 57Fe | 26 | 31 | 56,9353940 | стабилен | 1/2- |
| 58Fe | 26 | 32 | 57,9332756 | стабилен | 0+ |
| 59Fe | 26 | 33 | 58,9348755 | 44,495 сут | 3/2- |
| 60Fe | 26 | 34 | 59,934072 | 2,6 млн лет | 0+ |
| 61Fe | 26 | 35 | 60,936745 | 5,98 мин | 3/2- |
| 61mFe | 861 кэВ | 250 нс | 9/2+ | ||
| 62Fe | 26 | 36 | 61,936767 | 68 с | 0+ |
| 63Fe | 26 | 37 | 62,94037 | 6,1 с | 5/2- |
| 64Fe | 26 | 38 | 63,9412 | 2,0 с | 0+ |
| 65Fe | 26 | 39 | 64,94538 | 1,3 с | 1/2- |
| 65mFe | 364 кэВ | 430 нс | 5/2- | ||
| 66Fe | 26 | 40 | 65,94678 | 440 мс | 0+ |
| 67Fe | 26 | 41 | 66,95095 | 394 мс | 1/2- |
| 67mFe | 367 кэВ | 64 мкс | 5/2- | ||
| 68Fe | 26 | 42 | 67,95370 | 187 мс | 0+ |
| 69Fe | 26 | 43 | 68,95878 | 109 мс | 1/2- |
| 70Fe | 26 | 44 | 69,96146 | 94 мс | 0+ |
| 71Fe | 26 | 45 | 70,96672 | 30 мс | 7/2+ |
| 72Fe | 26 | 46 | 71,96962 | 10 мс | 0+ |
| 73Fe | 26 | 47 | > 633 нс | ||
| 74Fe | 26 | 48 | > 638 нс |
ПримерПравить
Если обозначить для данного момента времени число ядер способных к радиоактивному превращению через N, а промежуток времени через t2 — t1, где t1 и t2 — достаточно близкие моменты времени (t1 < t2), и число разлагающихся атомных ядер в этот отрезок времени через n, то n = KN(t2 — t1). Где коэффициент пропорциональности K = 0,693/T½ носит название константы распада. Если принять разность (t2 — t1) равной единице, т.е. интервал времени наблюдения равным единице, то K = n/N и, следовательно, константа распада показывает долю от наличного числа атомных ядер, испытывающих распад в единицу времени. Следовательно, распад совершается так, что в единицу времени распадается одна и та же доля от наличного числа атомных ядер, что определяет закон экспоненциального распада.
Величины периодов полураспада для различных изотопов различны; для некоторых, особенно быстро распадающихся, период полураспада может быть равным миллионным долям секунды, а для некоторых изотопов, как уран 238 и торий 232, он соответственно равен 4,498*109 и 1,389*1010 лет. Легко подсчитать число атомов урана 238, испытывающих превращение в данном количестве урана, например, в одном килограмме в течение одной секунды. Количество любого элемента в граммах, численно равное атомному весу, содержит, как известно, 6,02*1023 атомов. Поэтому согласно приведённой выше формуле n = KN(t2 — t1) найдём число атомов урана, распадающихся в одном килограмме в одну секунду, имея ввиду, что в году 365*24*60*60 секунд,
- $ \frac{0,693}{4,498*10^{9}*365*24*60*60} \frac{6,02*10^{23}}{238} * 1000 = 2*10^6 $.
Вычисления приводят к тому, что в одном килограмме урана в течение одной секунды распадается два миллиона атомов. Несмотря на такое огромное число, всё же скорость превращения ничтожно мала. Действительно, в секунду распадается следующая часть урана:
- $ \frac{2*10^6 * 238}{6,02*10^{23}*1000} = 7,9*10^{-19} $.
Таким образом, из наличного количества урана в одну секунду распадается его доля, равная
- $ 7,9 \over 10 000 000 000 000 000 000 $.
Обращаясь опять к основному закону радиоактивного распада KN(t2 — t1), т.е. к тому факту, что из наличного числа атомных ядер в единицу времени распадается всего одна и та же их доля и, имея к тому же ввиду полную независимость атомных ядер в каком-либо веществе друг от друга, можно сказать, что этот закон является статистическим в том смысле, что он не указывает какие именно атомные ядра подвергнутся распаду в данный отрезок времени, а лишь говорит об их числе. Несомненно, этот закон сохраняет силу лишь для того случая, когда наличное число ядер очень велико. Некоторые из атомных ядер распадутся в ближайший момент, в то время как другие ядра будут претерпевать превращения значительно позднее, поэтому когда наличное число радиоактивных атомных ядер сравнительно невелико, закон радиоактивного распада может и не выполняться во всей строгости.
Теория
Естественная радиоактивность — самопроизвольный распад атомных ядер, встречающихся в природе.
Искусственная радиоактивность — самопроизвольный распад атомных ядер, полученных искусственным путём через соответствующие ядерные реакции.
Ядро, испытывающее радиоактивный распад, и ядро, возникающее в результате этого распада, называют соответственно материнским и дочерним ядрами. Изменение массового числа и заряда дочернего ядра по отношению к материнскому описывается правилом смещения Содди.
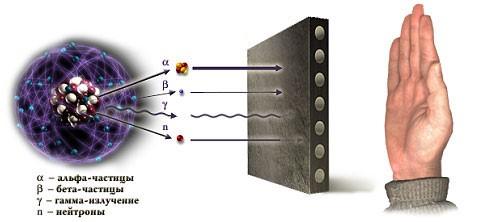
Распад, сопровождающийся испусканием альфа-частиц, назвали альфа-распадом; распад, сопровождающийся испусканием бета-частиц, был назван бета-распадом (в настоящее время известно, что существуют типы бета-распада без испускания бета-частиц, однако бета-распад всегда сопровождается испусканием нейтрино или антинейтрино). Термин «гамма-распад» применяется редко; испускание ядром гамма-квантов называют обычно изомерным переходом. Гамма-излучение часто сопровождает другие типы распада, когда в результате первого этапа распада возникает дочернее ядро в возбуждённом состоянии, затем испытывающее переход в основное состояние с испусканием гамма-квантов.
Энергетические спектры α-частиц и γ-квантов, излучаемых радиоактивными ядрами, прерывистые («дискретные»), а спектр β-частиц — непрерывный.
В настоящее время, кроме альфа-, бета- и гамма-распадов, обнаружены распады с испусканием нейтрона, протона (а также двух протонов), кластерная радиоактивность, спонтанное деление. Электронный захват, позитронный распад (или β+-распад), а также двойной бета-распад (и его виды) обычно считаются различными типами бета-распада.
Некоторые изотопы могут испытывать одновременно два или более видов распада. Например, висмут-212 распадается с вероятностью 64 % в таллий-208 (посредством альфа-распада) и с вероятностью 36 % в полоний-212 (посредством бета-распада).
Образовавшееся в результате радиоактивного распада дочернее ядро иногда оказывается также радиоактивным и через некоторое время тоже распадается. Процесс радиоактивного распада будет происходить до тех пор, пока не появится стабильное, то есть нерадиоактивное ядро. Последовательность таких распадов называется цепочкой распадов, а последовательность возникающих при этом нуклидов называется радиоактивным рядом. В частности, для радиоактивных рядов, начинающихся с урана-238, урана-235 и тория-232, конечными (стабильными) нуклидами являются соответственно свинец-206, свинец-207 и свинец-208.
Ядра с одинаковым массовым числом A (изобары) могут переходить друг в друга посредством бета-распада. В каждой изобарной цепочке содержится от 1 до 3 бета-стабильных нуклидов (они не могут испытывать бета-распад, однако не обязательно стабильны по отношению к другим видам радиоактивного распада). Остальные ядра изобарной цепочки бета-нестабильны; путём последовательных бета-минус- или бета-плюс-распадов они превращаются в ближайший бета-стабильный нуклид. Ядра, находящиеся в изобарной цепочке между двумя бета-стабильными нуклидами, могут испытывать и β−-, и β+-распад (или электронный захват). Например, существующий в природе радионуклид калий-40 способен распадаться в соседние бета-стабильные ядра аргон-40 и кальций-40:
- 1940K+e−→1840Ar+νe,{\displaystyle {}_{19}^{40}{\textrm {K}}+e^{-}\rightarrow {}_{18}^{40}{\textrm {Ar}}+\nu _{e},}
- 1940K→1840Ar+e++νe,{\displaystyle {}_{19}^{40}{\textrm {K}}\rightarrow {}_{18}^{40}{\textrm {Ar}}+e^{+}+\nu _{e},}
- 1940K→2040Ca+e−+ν¯e.{\displaystyle {}_{19}^{40}{\textrm {K}}\rightarrow {}_{20}^{40}{\textrm {Ca}}+e^{-}+{\bar {\nu }}_{e}.}
Временной интервал в радиоактивности
Момент развала частицы невозможно установить для данного конкретного атома. Для него это скорее «несчастный случай», нежели закономерность. Выделение энергии, характеризующее этот процесс, определяют как активность образца.
 Замечено, что она с течением времени меняется. Хотя отдельные элементы демонстрируют удивительное постоянство степени излучения, существуют вещества, активность которых уменьшается в несколько раз за достаточно короткий промежуток времени. Удивительное разнообразие! Возможно ли найти закономерность в этих процессах?
Замечено, что она с течением времени меняется. Хотя отдельные элементы демонстрируют удивительное постоянство степени излучения, существуют вещества, активность которых уменьшается в несколько раз за достаточно короткий промежуток времени. Удивительное разнообразие! Возможно ли найти закономерность в этих процессах?
Установлено, что существует время, в течение которого ровно половина атомов данного образца претерпевает распад. Этот интервал времени получил название «период полураспада». В чем смысл введения этого понятия?
Закон радиоактивного распада
Моделирование распада многих идентичных атомов. Начиная с 4 атомов (слева) и 400 (справа). Сверху показано число периодов полураспада.
Основная статья: Закон радиоактивного распада
Закон радиоактивного распада — закон, открытый Фредериком Содди и Эрнестом Резерфордом экспериментальным путём и сформулированный в 1903 году. Современная формулировка закона:
- dNdt=−λN,{\displaystyle {\frac {dN}{dt}}=-\lambda N,}
что означает, что число распадов за интервал времени t в произвольном веществе пропорционально числу N имеющихся в образце радиоактивных атомов данного типа.
Решение этого дифференциального уравнения с начальным условием N=N{\displaystyle N=N_{0}} при t={\displaystyle t=0:}
- N(t)=Ne−λt=Ne−tτ,{\displaystyle N(t)=N_{0}e^{-\lambda t}=N_{0}e^{-{\frac {t}{\tau }}},}
- где τ{\displaystyle \tau } — среднее время жизни радиоактивного атома.
В этом математическом выражении λ — постоянная распада, которая характеризует вероятность радиоактивного распада за единицу времени и имеет размерность с−1. Знак минус указывает на убывание числа радиоактивных ядер со временем. Закон выражает независимость распада радиоактивных ядер друг от друга и от времени: вероятность распада данного ядра в каждую следующую единицу времени не зависит от времени, прошедшего с начала эксперимента, и от количества ядер, оставшихся в образце.
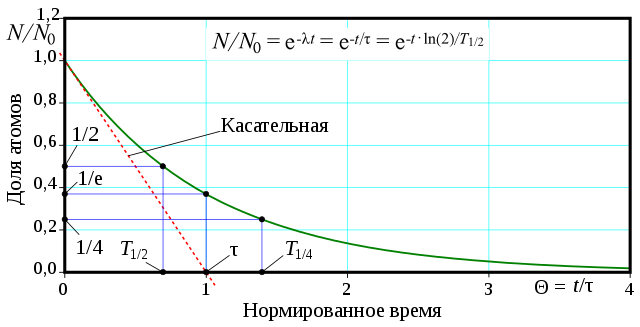 Экспоненциальная кривая радиоактивного распада: по оси абсцисс («оси x») — нормированное время Θ=tτ,{\displaystyle \Theta =t/\tau ,} по оси ординат («оси y») — доля NN{\displaystyle N/N_{0}} ещё нераспавшихся ядер или скорость распада в единицу времени I(Θ)=dNdΘ{\displaystyle \mathrm {I} (\Theta )=dN/d\Theta }
Экспоненциальная кривая радиоактивного распада: по оси абсцисс («оси x») — нормированное время Θ=tτ,{\displaystyle \Theta =t/\tau ,} по оси ординат («оси y») — доля NN{\displaystyle N/N_{0}} ещё нераспавшихся ядер или скорость распада в единицу времени I(Θ)=dNdΘ{\displaystyle \mathrm {I} (\Theta )=dN/d\Theta }
Этот закон считается основным законом радиоактивности, из него было извлечено несколько важных следствий, среди которых формулировки характеристик распада — среднее время жизни атома и период полураспада.
Константа распада радиоактивного ядра в большинстве случаев практически не зависит от окружающих условий (температуры, давления, химического состава вещества и т. п.). Например, твёрдый тритий T2 при температуре в несколько кельвинов распадается с той же скоростью, что и газообразный тритий при комнатной температуре или при температуре в тысячи кельвинов; тритий в составе молекулы T2 распадается с той же скоростью, что и в составе, например, аминокислоты валина с замещёнными атомами водорода атомами трития.
Слабые изменения константы распада в лабораторных условиях обнаружены лишь для электронного захвата — доступные в лаборатории температуры и давления, а также изменение химического состава способны несколько изменять плотность электронного облака в окружении ядра, что приводит к изменению скорости распада на доли процента. Однако в достаточно жёстких условиях (высокая ионизация атома, высокая плотность электронов, высокий химический потенциал нейтрино, сильные магнитные поля), труднодостижимых в лаборатории, но реализующихся, например, в ядрах звёзд, другие типы распадов тоже могут изменять свою вероятность.
Постоянство константы радиоактивного распада позволяет измерять возраст различных природных и искусственных объектов по результатам измерения концентрации входящих в их состав радиоактивных ядер и концентрации накопленных продуктов распада. Разработан ряд методов радиоизотопного датирования, позволяющих измерять возраст объектов в диапазоне от единиц до миллиардов лет; среди них наиболее известны радиоуглеродный метод, уран-свинцовый метод, уран-гелиевый метод, калий-аргоновый метод и др.