Спин (физика)

Суммарное спиновое число

Суммарное спиновое число равно сумме ms всех электронов атома. Это условие впервые было сформулировано Хундом и известно как правило Хунда.
 

Такая перестройка приведет к возрастанию суммарного спинового числа ( Ss), как это показано на рис. 38, по оси ординат которого даны спиновые числа для возбужденных и невозбужденных состояний.
 

Суммарное электронное состояние характеризуют также суммарным спиновым числом S, причем последнее изображается в виде числа 2S 4s 1, записанного в виде индекса слева сверху от символа орбитального состояния. Это число указывает, сколько имеется независимых спиновых состояний, и называется мулыпиплетностью.
 

Суммарное электронное состояние характеризуют также суммарным спиновым числом S, причем последнее изображается в виде числа 25 1, записанного в виде индекса сверху слева от символа орбитального состояния. Это число указывает, сколько имеется независимых спиновых состояний, и называется мультиплетностью.
 

Порядок заполнения орбиталей данного подслоя подчиняется правилу Хунда: суммарное спиновое число электронов данного подслоя должно быть максимальным.
 

Заполнение электронами атомных р-орбиталей одного подуровня происходит таким образом, чтобы их суммарное спиновое число было максимальным.
 

При заполнении ( заселении) электронами подуровней нужно соблюдать правило Гунда: суммарное спиновое число электронов данного подуровня должно быть максимальным. Правило Гунда получено на основании спектральных исследований и формулируется вообще более сложно. Оно полностью применимо для атомов в их устойчивом или стабильном состоянии, а также и для возбужденных атомов.
 

При заполнении ( заселении) электронами подуровней нужно соблюдать правило Гунда: суммарное спиновое число электронов данного подуровня должно быть максимальным. Правило Гунда получено на основании спектральных исследований и формулируется вообще более сложно. Оно полностью применимо для атомов в их устойчивом или стабильном, состоянии, а также и для возбужденных атомов. Рассмотрим правило Гунда на примере заполнения подуровня 2р, который имеет три орбитали: pz; px; ру. Эти орбитали можно условно представить в виде трех клеточек, заполненных тремя электронами с различными спиновыми моментами.
 

При заполнении ( заселении) электронами подуровней нужно соблюдать правило Гунда: суммарное спиновое число электронов данного подуровня должно быть максимальным. Правило Гунда получено на основании спектральных исследований и формулируется вообще более сложно. Оно полностью применимо для атомов в их устойчивом, или стабильном, состоянии.
 

Поскольку для отдельного электрона спиновое квантовое число s 1 / 2, максимальное значение суммарного спинового числа равно просто половине количества электронов, входящих в расчет, а минимальное — 1 / 2 для нечетного количества электронов и нулю для четного.
 

При возбуждении атомов их электроны переходят на более высокие подуровни и соответственно с этим увеличивается их суммарное спиновое число ( Ssj), так как при этом разрушаются уже готовые электронные пары. Энергия возбуждения атома в пределах одного и того же уровня, как правило, невелика. Возбуждение может происходить за счет изменения энергии при образовании молекул или за счет энергии химических реакций. Степень возбуждения атома определяется наличием свободных орбиталей в пределах уровней, имеющихся в атоме. Чем больше главное квантовое число п и чем сложнее строение уровня ( см. рис. 17, табл. 2.8), тем больше существует возможностей для возбуждения атомов.
 

При возбуждении атомов их электроны переходят на более высокие подуровни и соответственно с этим увеличивается их суммарное спиновое число ( 2s), так как при этом разрушаются уже готовые электронные пары. Энергия возбуждения атома в пределах одного и того же уровня, как правило, невелика.
 

Спин классических систем

Понятие спина было введено в квантовой теории.
Тем не менее, в релятивистской механике можно определить спин классической (не квантовой)
системы как собственный момент импульса.
Классический спин является 4-вектором и определяется следующим образом:

Sν=12εναβγLαβUγ,{\displaystyle S_{\nu }={\frac {1}{2}}\,\varepsilon _{\nu \alpha \beta \gamma }\,L^{\alpha \beta }\,U^{\gamma },}

где

Lαβ=∑(xαpβ−xβpα){\displaystyle L^{\alpha \beta }=\sum (x^{\alpha }p^{\beta }-x^{\beta }p^{\alpha })} — тензор полного момента импульса системы (суммирование проводится по всем частицам системы);

Uα=PαM{\displaystyle U^{\alpha }=P^{\alpha }/M} — суммарная 4-скорость системы, определяемая при помощи суммарного 4-импульса Pα=∑pα{\displaystyle P^{\alpha }=\sum p^{\alpha }} и массы M системы;

εναβγ{\displaystyle \varepsilon _{\nu \alpha \beta \gamma }} — тензор Леви-Чивиты.

В силу антисимметрии тензора Леви-Чивиты, 4-вектор спина всегда ортогонален к 4-скорости Uα.{\displaystyle U^{\alpha }.} В системе отсчёта, в которой суммарный импульс системы равен нулю, пространственные компоненты спина совпадают с вектором момента импульса, а временная компонента равна нулю.

Именно поэтому спин называют собственным моментом импульса.

В квантовой теории поля это определение спина сохраняется. В качестве момента импульса и суммарного импульса выступают интегралы движения соответствующего поля. В результате процедуры вторичного квантования 4-вектор спина становится оператором с дискретными собственными значениями.

Спиновое квантовое число

Спин элементарных частиц

В теории элементарных частиц обычно предполагается, что фотон, электрон и кварки не делятся на более мелкие
части и являются самыми «элементарными». Однако спин, который приписывается
этим частицам, слишком велик, чтобы его можно было объяснить вращением
составляющего вещества при известных оценках размеров частиц. Поэтому для этих
частиц спин полагается некоторым внутренним свойством, наподобие массы и
заряда, требующим особого, пока ещё не известного обоснования.

В квантовой механике спиновый момент импульса любой системы квантуется.
Амплитуда или длина вектора спинового момента в каждом состоянии равна:

где есть постоянная Дирака, а спиновое квантовое число s является положительным целым или полуцелым числом (0, 1/2, 1, 3/2, 2, …) и зависит от типа
частицы. В противоположность этому орбитальный момент импульса имеет только
целые квантовые числа.

Спин составных частиц

К составным частицам можно отнести атомные ядра, состоящие из нуклонов, а
также адроны, согласно кварковой концепции
состоящие из кварков. Спин составной частицы находится векторным суммированием
орбитальных и спиновых моментов импульса всех составляющих её частиц, с учётом
правил квантового сложения, и также квантуется, как любой момент импульса. В
квантовой механике каждая составная частица имеет некоторый минимально
возможный спин, не обязательно равный нулю (в этом состоянии моменты импульса
составляющих частиц частично компенсируют друг друга, уменьшая спин составной
частицы до минимума). Если же моменты импульса составляющих частиц
складываются, то это может приводить к состояниям, в которых составная частица
имеет значительный спин. Так, одним из наибольших спинов среди адронов обладает
барионный резонанс Δ(2950) со спином 15/2. Спин
ядер из-за их относительно больших размеров может превышать 20 .

В качестве других примеров можно привести Δ-барион
и какой-либо нуклон, протон или нейтрон. В кварковой
теории у Δ-бариона спины всех трёх кварков
складываются, давая спин 3/2. В нуклоне спины двух кварков противоположны и
вычитаются, и спин 1/2 нуклона равен спину третьего кварка. Картина однако усложняется тем, что в нуклонах кроме кварков
предполагаются глюоны как переносчики взаимодействия,
а также виртуальные частицы. Вследствие этого распределение момента импульса
между кварками и глюонами в адронах точно не
определено.

Спин атомов и молекул

Размеры атомов и молекул много больше размеров атомных ядер, так что спин
какого-либо атома определяется его электронной оболочкой. В заполненных атомных
оболочках количество электронов чётно и их суммарный момент импульса равен
нулю. Поэтому за спин атомов и молекул ответственны неспаренные
электроны, находящиеся обычно на внешней оболочке. Считается, что именно спин неспаренных электронов приводит к явлению парамагнетизма.

Ниже указаны спины некоторых элементарных и составных частиц.

Ссылки

1. B. Friedrich, D. Herschbach.
   Stern
   and Gerlach: How a Bad Cigar Helped Reorient
   Atomic Physics. Physics Today, 2003, Vol. 56, issue 12, page 53.
2. W. Pauli «The Connection Between Spin and Statistics», Phys. Rev. 58, 716-722 (1940), pdf.
3. W.J. Marciano, A.I. Sanda.
   Exotic decays of the muon and heavy leptons in gauge theories. Physics Letters, 1977, Vol. B67, issue 3, page 303–305.
4. B.W. Lee, R.E. Shrock.
   Natural suppression of symmetry violation in gauge theories: Muon- and
   electron-lepton-number nonconservation. Physical Review, 1977, Vol. D16, issue 5, page 1444–1473.
5. K. Fujikawa, R.
   E. Shrock. Magnetic Moment of a Massive Neutrino
   and Neutrino-Spin Rotation. Physical Review Letters, 1980, Vol. 45, issue 12, page 963–966.
6. N.F. Bell et al. How Magnetic is
   the Dirac Neutrino? Physical Review Letters, 2005, Vol. 95, issue 15, page
   151802. arXiv hep-ph/0504134.
7. Spintronics. Feature Articleв Scientific American, June 2002.
8. Федосин С.Г. Физические теории и бесконечная
   вложенность материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289
   назв. ISBN 978-5-9901951-1-0.
9. Федосин С. Г. Физика и философия подобия от преонов
   до метагалактик, Пермь: Стиль-МГ, 1999, ISBN 5-8131-0012-1, 544 стр.,
   Табл.66, Ил.93, Библ. 377 назв.
10. Комментарии к книге: Федосин
    С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 844
    стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
11. Федосин С.Г. Современные проблемы физики. В
    поисках новых принципов, М: Эдиториал УРСС,
    2002, ISBN 5-8360-0435-8, 192 стр., Ил.26, Библ. 50 назв.

Использование концепции спина в науке и технике

Понятие спина широко используется в ядерном магнитном резонансе в химической
спектроскопии, в электронном парамагнитном резонансе в химической и физической
спектроскопии, в магниторезонансных измерениях плотности протонных спинов с
целью сканирования внутренних органов в медицине, в технологиях современных
компьютерных жёстких дисков на основе гигантского магниторезистивного эффекта.

Спин рассматривается как возможный носитель двоичной информации в спиновых
транзисторах. Электроника, связанная с такими транзисторами, носит название спинтроника.

Спин и принцип Паули оказываются необходимыми в квантовой механике для
объяснения ряда явлений и закономерностей, таких например, как периодическая
таблица Дмитрия Менделеева.

Что такое спин — на примерах

Пример объекта, который требует поворота на 720 градусов для возврата в начальное положение.

Хотя термин «спин» относится только к квантовым свойствам частиц, свойства некоторых циклически действующих макроскопических систем тоже могут быть описаны неким числом, которое показывает, на сколько частей нужно разделить цикл вращения некоего элемента системы, чтобы она вернулась в состояние, неотличимое от начального.

Легко представить себе спин, равный 0: это точка — она со всех сторон выглядит одинаково, как её ни крути.

Примером спина, равного 1, может служить большинство обычных предметов без какой-либо симметрии: если такой предмет повернуть на 360 градусов, то этот предмет вернётся в своё первоначальное состояние. Для примера — можно положить ручку на стол, и после поворота на 360° ручка опять будет лежать так же, как и до поворота.

В качестве примера спина, равного 2 можно взять любой предмет с одной осью центральной симметрии: если его повернуть на 180 градусов, он будет неотличим от исходного положения, и получается за один полный оборот он становится неотличим от исходного положения 2 раза. Примером из жизни может служить обычный карандаш, только заточенный с двух сторон или не заточенный вообще — главное чтобы был без надписей и однотонный — и тогда после поворота на 180° он вернется в положение, не отличимое от исходного. Хокинг в качестве примера приводил обычную игральную карту типа короля или дамы

А вот с полуцелым спином, равным 1/₂ немножко сложнее: это получается, что в исходное положение система возвращается после 2-х полных оборотов, то есть после поворота на 720 градусов. Примеры:

Если взять ленту Мёбиуса и представить, что по ней ползет муравей, тогда, сделав один оборот (пройдя 360 градусов), муравей окажется в той же точке, но с другой стороны листа, а чтобы вернуться в точку, откуда он начал, придётся пройти все 720 градусов.

Четырёхтактный двигатель возвращается в исходное состояние при повороте коленчатого вала на 720 градусов, что является неким аналогом полуцелого спина

четырехтактный двигатель внутреннего сгорания. При повороте коленчатого вала на 360 градусов поршень вернётся в исходное положение (например, верхнюю мёртвую точку), но распределительный вал вращается в 2 раза медленнее и совершит полный оборот при повороте коленчатого вала на 720 градусов. То есть при повороте коленчатого вала на 2 оборота двигатель внутреннего сгорания вернётся в то же состояние. В этом случае третьим измерением будет положение распределительного вала.

На подобных примерах можно проиллюстрировать сложение спинов:

• Два заточенных только с одной стороны одинаковых карандаша («спин» каждого — 1), скреплённые боковыми сторонами друг с другом так, что острый конец одного будет рядом с тупым концом другого (↑↓). Такая система вернётся в неотличимое от начального состояния при повороте всего на 180 градусов, то есть «спин» системы стал равным двум.
• Многоцилиндровый четырёхтактный двигатель внутреннего сгорания («спин» каждого из цилиндров которого равен 1/2). Если все цилиндры работают одинаково, то состояния, при которых поршень находится в начале такта рабочего хода в любом из цилиндров, будут неотличимы. Следовательно, двухцилиндровый двигатель будет возвращаться в состояние, неотличимое от исходного, через каждые 360 градусов (суммарный «спин» — 1), четырёхцилиндровый — через 180 градусов («спин» — 2), восьмицилиндровый — через 90 градусов («спин» — 4).

Ориентация спина

Квантовое число проекции спина и мультиплетность

Поскольку спин является вектором момента импульса, он имеет и амплитуду и направление в пространстве. В квантовой механике
используется понятие о проекции момента импульса на некоторую выделенную ось
(обычно направление этой оси в пространстве задаётся внешним магнитным полем).
Пусть выделенное направление фиксируется осью zиспользуемой системы отсчёта. Тогда возможные
проекции спина на эту ось имеют значения:

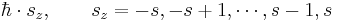
где sесть спиновое квантовое число для частицы или системы частиц. Общее
число проекций спина s_zравно 2s+1. В стандартной теории в
приближении спин-орбитальной связи число 2s+1называется мультиплетностью спиновой системы.
В частности, для частиц со спином 1/2получается
только два значения для проекции спина: s_z
= +1/2 и s_z = -1/2. Отсюда следует,
что для электрона в водородоподобном атоме мультиплетность равна 2, а спектры
таких атомов имеют дублетную природу. При наличии двух электронов, как это
происходит в гелии, суммарный спин обоих электронов равен 0 либо 1.
Соответственно, мультиплетность будет равна 1 для парагелия с одиночными
линиями в спектре, и равна 3 для ортогелия с триплетными линиями в спектре.

Вектор спина

В каждом квантовом состоянии можно ввести вектор спина ,
чьими компонентами являются ожидаемые значения проекций спина на оси системы
координат .
Этот вектор указывает «направление» спина, соответствующее в
классическом пределе оси вращения. В квантовомеханических
вычислениях вектор спина имеет особенность – его компоненты s_x,s_yиs_zне могут быть измерены одновременно из-за квантового принципа неопределённости Гейзенберга.
Однако для статистически больших наборов частиц при одинаковых начальных
квантовых состояниях, как это имеет место в опыте Штерна — Герлаха,
вектор спина и связанный с ним вектор магнитного момента имеют хорошо
определённое экспериментально направление – оно задаётся той ориентацией
детектора, при которой отмечается наибольшее
количество частиц из всего используемого набора.

Вследствие связи между спином и его магнитным моментом внешнее магнитное
поле будет приводить к прецессии спина вдоль магнитного поля. Этот эффект
аналогичен классическому гироскопическому эффекту – магнитное поле действует на
магнитный дипольный момент и создаёт крутящий момент, который прикладывается к
спиновому механическому моменту частицы и приводит к прецессии оси вращения и
спина частицы.

В квантовой механике спин описывается не просто вектором как классический
момент импульса, а с помощью математических объектов – спиноров. Поведение
векторов и спиноров при вращении координат различается. Например, каждое
вращение частицы со спином 1/2 на 360 градусов приводит частицу не в прежнее
состояние, а в состояние с противоположной квантовомеханической
фазой. Для частицы с нулевым спином её квантовое состояние при вращении не
меняется. Если же у частицы спин равен 2, то при вращении на 180 градусов она
получает прежнее квантовое состояние.

Спиновый магнитный момент

Спин является частью полного механического момента импульса частицы, и если
последняя заряжена, то спину по формулам классической электродинамики можно
поставить в соответствие определённый магнитный дипольный момент. При этом
часто используется так называемое гиромагнитное отношение как отношение
магнитного момента к механическому моменту. Для частицы с массой m, зарядом qи спином Sспиновый магнитный момент μ равен:

где безразмерная величина gназывается g-фактором. Для чисто орбитального
(например, кругового) вращения элементов заряженного вещества частицы вокруг
оси g-фактор должен быть равен 1. У электрона g-фактор почти точно равен 2, что
существенно отличает спин от орбитального вращения. Отличие g-фактора электрона
от 2 в квантовой электродинамике обосновывается как следствие взаимодействия
заряда электрона с окружающим электромагнитным полем, включая самодействие поля
электрона. За счёт спинового магнитного момента частицы могут взаимодействовать
друг с другом и с внешними магнитными полями.

Как правило принимается, что нейтрино электрически
нейтральны, но при наличии некоторой ненулевой массы покоя у них не исключается
наличие магнитного момента. Формула
для предполагаемого магнитного момента нейтрино имеет вид:

где есть масса-энергия
нейтрино в электронвольтах, –
магнетон Бора. Если исходить из оценок массы-энергии нейтрино, не превышающих
значение 1 eV, то из соображений ограниченности электромагнитной энергии по
сравнению с энергией покоя ожидается, что магнитный момент нейтрино не
превышает 10−14.
Из имеющихся экспериментальных данных магнитный момент нейтрино не превышает
1,2 × 10–10 от величины магнитного момента электрона.

Наличие спина у составных частиц приводит к соответствующему спиновому
магнитному моменту. Многие нейтральные адроны, невзирая на равенство нулю у них
суммарного заряда, обладают магнитным моментом, причём направление магнитного
момента обычно противоположно спину. Это ясно указывает на их сложную
внутреннюю электромагнитную структуру. С точки зрения кварков, которым
приписываются различные заряды, магнитные моменты адронов приблизительно могут
быть получены как комбинации спиновых и орбитальных магнитных моментов
составляющих адроны кварков.

В веществе большинства тел магнитные моменты атомов направлены случайным
образом в различные стороны и взаимно вычитают друг друга, обращая суммарное
магнитное поле в нуль. В ферромагнитных материалах
ниже температуры Кюри возникает внутренняя магнитная упорядоченность за счёт
доменной структуры. В каждом домене магнитные моменты атомов выстраиваются
приблизительно параллельно, усиливая общее магнитное поле. В свою очередь
магнитные поля доменов суммируются векторно, приводя
к достаточно устойчивой намагниченности ферромагнетиков и превращая их в
магниты.

Магнитная упорядоченность возникает и под действием внешнего магнитного
поля. В парамагнитных материалах магнитные моменты атомов устанавливаются вдоль
приложенного магнитного поля, тогда как в диамагнитных веществах атомные
магнитные моменты направлены против поля и ослабляют его. Электронный
парамагнетизм есть следствие ориентации электронных магнитных моментов, которые
начинают прецессировать вдоль направления поля. Диамагнетизм вытекает из
действия закона электромагнитной индукции, согласно которому при изменении
магнитного потока в системе зарядов возникает электродвижущая сила.
Появляющееся по действием
этой силы движение зарядов приводит к магнитному полю, направленному
противоположно исходному магнитному полю (правило Ленца). Считается, что
существенная доля магнитных моментов атомов связана со спином электронов, хотя
вклады в магнитные эффекты делают и орбитальные магнитные моменты электронов.