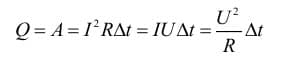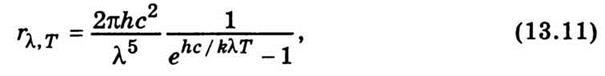Фундаментальные физические постоянные

Фундаментальные физические постоянные

Величина	Символ	Значение	Прим.
скорость света в вакууме	c{\displaystyle \ c}	299 792 458 м·с−1= 2,99792458·108 м·с−1	точно
гравитационная постоянная	G{\displaystyle \ G}	6,674 08(31)·10−11 м3·кг−1·с−2	a
постоянная Планка (элементарный квант действия)	h{\displaystyle \ h}	6,626 070 040(81)·10−34 Дж·с	a
постоянная Дирака (приведённая постоянная Планка)	ℏ=h2π{\displaystyle \hbar =h/2\pi }	1,054 571 800(13)·10−34 Дж·с	a
элементарный заряд	e{\displaystyle \ e}	1,602 176 6208(98)·10−19 Кл = 4,803 204 673(29)·10−10абсол. электростат. ед.	a
постоянная Больцмана	k{\displaystyle \ k}	1,380 648 52(79)·10−23 Дж·К−1	a

Векторные и скалярные величины

В физике существует два вида физических величин: векторные и скалярные. Основное их отличие в том, что векторные физические величины имеют направление. Что значит физическая величина имеет направление? Например, число картофелин в мешке, мы будем называть обыкновенными числами, или скалярами. Еще одним примером такой величины может служить температура. Другие очень важные в физике величины имеют направление, это, например, скорость; мы должны задать не только быстроту перемещения тела, но и путь, по которому оно движется. Импульс и сила тоже имеют направление, как и смещение: когда кто-нибудь делает шаг, можно сказать не только, как далеко он шагнул, но и куда он шагает, то есть определить направление его движения. Векторные величины лучше запомнить.

Некоторые уравнения электродинамики в СИ

В материальных уравнениях, в вакууме, через электрическую постоянную связаны вектор электрической индукции D{\displaystyle \mathbf {D} } и вектор напряжённости электрического поля E{\displaystyle \mathbf {E} }:

D=ε E.{\displaystyle \mathbf {D} =\varepsilon _{0}\ \mathbf {E} .}

Она также входит в запись закона Кулона (тоже в вакууме):

F12=14πε⋅q1q2r122r12r12.{\displaystyle \mathbf {F} _{12}={\frac {1}{4\pi \varepsilon _{0}}}\cdot {\frac {q_{1}q_{2}}{r_{12}^{2}}}{\frac {\mathbf {r} _{12}}{r_{12}}}.}

При использовании СИ произведение электрической постоянной на относительную диэлектрическую проницаемость называют абсолютной диэлектрической проницаемостью.

Некоторые другие физические постоянные

Название	Символ	Значение	Прим.
Массы элементарных частиц: масса электрона	me{\displaystyle \ m_{e}}	9,109 383 7015(28)⋅10−31 кг (абсол.) = 0,000548579909065(16) а.е.м. (относит.)
масса протона	mp{\displaystyle \ m_{p}}	1,672 621 923 69(51)⋅10−27 кг = 1,007276466621(53) а.е.м.
масса нейтрона	mn{\displaystyle \ m_{n}}	1,674 927 498 04(95)⋅10−27 кг= 1,008 664 915 60(57) а.е.м.
М протон плюс электрон (абсолютная масса атома водорода 1H)	mp+e{\displaystyle \ m_{p+e}}	≈ 1,673 5328⋅10−27 кг = 1,007825 а.е.м. (относит.)
магнитный момент электрона	μe{\displaystyle \mu _{e}}	−928,476 470 43(28)⋅10−26 Дж·Тл−1
магнитный момент протона	μp{\displaystyle \mu _{p}}	1,410 606 797 36(60)⋅10−26 Дж·Тл−1
магнетон Бора	μB=eℏ2me{\displaystyle \mu _{B}=e\hbar /2m_{e}}	927,401 007 83(28)⋅10−26 Дж·Тл−1
ядерный магнетон	μN{\displaystyle \mu _{N}}	5,050 783 7461(15)⋅10−27 Дж·Тл−1
g-фактор свободного электрона	ge=2μeμB{\displaystyle g_{e}=2\mu _{e}/\mu _{B}}	2,002 319 304 362 56(35)
гиромагнитное отношение протона	γp=2μpℏ{\displaystyle \gamma _{p}=2\mu _{p}/\hbar }	2,675 221 8744(11)⋅108 с−1·Тл−1
постоянная Фарадея	F=NAe{\displaystyle \ F=N_{A}e}	96 485,332 12… Кл·моль−1
универсальная газовая постоянная	R=kNA{\displaystyle \ R=kN_{A}}	8,314 462 618… Дж·К−1·моль−1 ≈ 0,082057 л·атм·К−1·моль−1
молярный объём идеального газа (при 273,15 К, 101,325 кПа)	Vm{\displaystyle \ V_{m}}	22,413 969 54… ⋅10−3 м³·моль−1
стандартное атмосферное давление (н.у.)	атм	101 325 Па	точно
боровский радиус	a=α(4πR∞){\displaystyle a_{0}=\alpha /(4\pi R_{\infty })}	0,529 177 210 903(80)⋅10−10 м
энергия Хартри	Eh=2R∞hc{\displaystyle E_{h}=2R_{\infty }hc}	4,359 744 722 2071(85)⋅10−18 Дж
постоянная Ридберга	R∞=α2mec2h{\displaystyle R_{\infty }=\alpha ^{2}m_{e}c/2h}	10 973 731,568 160(21) м−1
первая радиационная постоянная	c1=2πhc2{\displaystyle c_{1}=2\pi hc^{2}}	3,741 771 852… ⋅10−16 Вт·м²
вторая радиационная постоянная	c2=hck{\displaystyle c_{2}=hc/k}	1,438 776 877… ⋅10−2 м·К
постоянная Стефана-Больцмана	σ=(π260)k4ℏ3c2{\displaystyle \sigma =(\pi ^{2}/60)k^{4}/\hbar ^{3}c^{2}}	5,670 374 419… ⋅10−8 Вт·м−2·К−4
постоянная Вина	b=c24,965114231…{\displaystyle b=c_{2}/4,965114231…}	2,897 771 955… ⋅10−3м·К
стандартное ускорение свободного падения на поверхности Земли (усреднённое)	gn{\displaystyle g_{n}}	9,806 65 м·с−2	точно
Температура тройной точки воды	T{\displaystyle T_{0}}	273,16 K

Expeditionary Fighting Vehicle (EFV)

Боевая машина Expeditionary Fighting Vehicle. /Фото: naked-science.ru

Еще одна амбициозная задумка, однако теперь в виде одного образца техники. Проект Expeditionary Fighting Vehicle должен был подарить американской армии инновационную амфибийную боевую машину, удовлетворяющую нужды морских пехотинцев США. На первых порах, EFV была довольно перспективной: в ней объединились немалая боевая мощь, хорошая защита и приличная скорость.

Однако на этапе испытаний был выявлен ряд недостатков, которые фактически поставили крест на массовом производстве EFV. Так, например, машина никак не могла разогнаться до максимальной скорости на воде, ее силовая установка оказалась весьма капризной. Кроме того, морских пехотинцев откровенно оттолкнула цена амфибии – около 25 млн долларов за единицу. Даже сам концепт EFV подвергся критике, ведь к тому времени противокорабельные средства были достаточно эффективными, и защита машины оказывалась перед ними уязвимой.

2.1. Системы единиц физических величин

Понятие о физической величине — одно из наиболее общих в физике и метрологии. Под физической величиной понимается свойство, общее в качественном отношении для многих физических объектов (физических систем, их состояний и происходящих в них процессов), но в количественном отношении индивидуальное для каждого объекта. Так, все тела обладают массой и температурой, но для каждого из них эти параметры различны. То же самое можно сказать и о других величинах — электрическом токе, вязкости жидкостей или потоке излучения.

Для того чтобы можно было установить различия в количественном содержании свойств в каждом объекте, отображаемых физической величиной, вводится понятие размера физической величины.

Исторически первой системой единиц физических величин была принятая в 1791 г. Национальным собранием Франции метрическая система мер. Она не являлась еще системой единиц в современном понимании, а включала в себя единицы длин, площадей, объемов, вместимостей и веса, в основу которых были положены две единицы: метр и килограмм.

В 1832 г. немецкий математик К. Гаусс предложил методику построения системы единиц как совокупности основных и производных. Он построил систему единиц, в которой за основу были приняты три произвольные, независимые друг от друга единицы — длины, массы и времени. Все остальные единицы можно было определить с помощью этих трех. Такую систему единиц, связанных определенным образом с тремя основными, Гаусс назвал абсолютной системой. За основные единицы он принял миллиметр, миллиграмм и секунду.

В дальнейшем с развитием науки и техники появился ряд систем единиц физических величин, построенных по принципу, предложенному Гауссом, базирующихся на метрической системе мер, но отличающихся друг от друга основными единицами.

Рассмотрим главнейшие системы единиц физических величин .

Система СГС. Система единиц физических величин СГС, в которой основными единицами являются сантиметр как единица длины, грамм как единица массы и секунда как единица времени, была установлена в 1881 г.

Система МКГСС. Применение килограмма как единицы веса, а в последующем как единицы силы вообще, привело в конце XIX века к формированию системы единиц физических величин с тремя основными единицами: метр — единица длины, килограмм-сила — единица силы и секунда — единица времени.

Система МКСА. Основы этой системы были предложены в 1901 г. итальянским ученым Джорджи. Основными единицами системы МКСА являются метр, килограмм, секунда и ампер.

Связь между температурой и энергией

В однородном идеальном газе, находящемся при абсолютной температуре T{\displaystyle T}, энергия, приходящаяся на каждую поступательную степень свободы, равна, как следует из распределения Максвелла, kT2{\displaystyle kT/2}. При комнатной температуре (300 К) эта энергия составляет 2,07×10−21{\displaystyle 2{,}07\times 10^{-21}} Дж, или 0,025851 эВ. В одноатомном идеальном газе каждый атом обладает тремя степенями свободы, соответствующими трём пространственным осям, что означает, что на каждый атом приходится энергия в 32kT{\displaystyle {\frac {3}{2}}kT}.

Зная тепловую энергию, можно вычислить среднеквадратичную скорость атомов, которая обратно пропорциональна квадратному корню атомной массы. Среднеквадратичная скорость при комнатной температуре изменяется от 1370 м/с для гелия до 240 м/с для ксенона. В случае молекулярного газа ситуация усложняется, например, двухатомный газ имеет 5 степеней свободы — 3 поступательных и 2 вращательных (при низких температурах, когда не возбуждены колебания атомов в молекуле и не добавляются дополнительные степени свободы).

Примечания

1. ↑
2.  (недоступная ссылка). physics.nist.gov. Дата обращения 28 июня 2015.
3.  (недоступная ссылка). physics.nist.gov. Дата обращения 28 июня 2015.
4.  (недоступная ссылка). physics.nist.gov. Дата обращения 28 июня 2015.
5. из соотношения E = mc2
6. из отношения, определяющего зависимость свободной энергии от концентрации (парциального давления): G=G∘+RT ln(pp∘){\displaystyle G=G^{\circ }+RT~\mathrm {ln} \left({\frac {p}{\displaystyle {p^{\circ }}}}\right)} 2,30259 — модуль перехода (логарифмы)
7. из соотношения E=hv=hcv¯{\displaystyle E=hv=hc{\bar {v}}}, где v¯{\displaystyle {\bar {v}}} выражено в обратных сантиметрах см−1
8. . physics.nist.gov.

Колебания

Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω:

Решение предыдущего уравнения является уравнением движения для гармонических колебаний и имеет вид:

Период колебаний вычисляется по формуле:

Частота колебаний:

Циклическая частота колебаний:

Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:

Максимальное значение скорости при гармонических механических колебаниях:

Зависимость ускорения от времени при гармонических механических колебаниях:

Максимальное значение ускорения при механических гармонических колебаниях:

Циклическая частота колебаний математического маятника рассчитывается по формуле:

Период колебаний математического маятника:

Циклическая частота колебаний пружинного маятника:

Период колебаний пружинного маятника:

Максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:

Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:

Взаимосвязь энергетических характеристик механического колебательного процесса:

Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:

Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:

Циклическая частота колебаний в электрическом колебательном контуре:

Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:

Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:

Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:

Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:

Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:

Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин следующим образом. Действующее значение силы тока:

Действующее значение напряжения:

Мощность в цепи переменного тока:

Трансформатор

Если напряжение на входе в трансформатор равно U₁, а на выходе U₂, при этом число витков в первичной обмотке равно n₁, а во вторичной n₂, то выполняется следующее соотношение:

Коэффициент трансформации вычисляется по формуле:

Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):

В неидеальном трансформаторе вводится понятие КПД:

Волны

Длина волны может быть рассчитана по формуле:

Разность фаз колебаний двух точек волны, расстояние между которыми l:

Скорость электромагнитной волны (в т.ч. света) в некоторой среде:

Скорость электромагнитной волны (в т.ч. света) в вакууме постоянна и равна с = 3∙108 м/с, она также может быть вычислена по формуле:

Скорости электромагнитной волны (в т.ч. света) в среде и в вакууме также связаны между собой формулой:

При этом показатель преломления некоторого вещества можно рассчитать используя формулу:

Определение энтропии

Энтропия термодинамической системы определяется как величина, пропорциональная натуральному логарифму от числа различных микросостояний Z{\displaystyle Z}, соответствующих данному макроскопическому состоянию (например, состоянию с заданной полной энергией).

S=kln⁡Z.{\displaystyle S=k\ln Z.}

Коэффициент пропорциональности k{\displaystyle k} и есть постоянная Больцмана. Это выражение, определяющее связь между микроскопическими (Z{\displaystyle Z}) и макроскопическими состояниями (S{\displaystyle S}), выражает центральную идею статистической механики.

Автомобиль-вертолёт

Один из проектов летающего автомобиля. /Фото: reddit.com

И до Второй мировой войны, и во время нее инженеры пытались создать такое оружие или военную технику, чьи способности и характеристики кажутся впечатляющими даже сейчас. Одним из таких откровенно странных проектов можно смело назвать разработку нового летательного аппарата в виде гибрида вертолета и автомобиля.

Подобную машину решили спроектировать военные инженеры британской армии. В конечном итоге у них получился агрегат, который представлял собой внедорожник, оснащенный хвостом и несущим винтом от вертолёта. Поразительно, но эта машина действительно неплохо летала. Однако крест на развитии необычного концепта поставила банальная практичность: быстро стало ясно, что транспортировка наземной техники осуществляется немного проще посредством самолётов, нежели путем создания десятков и сотен гибридов.

Проблема фундаментальных физических констант

Проблема фундаментальных физических констант естественным образом возникла на основе большого количества накопленных результатов исследований в области физики элементарных частиц. Благодаря этому направлению исследований появилось большое количество новых фундаментальных физических постоянных, которые уже выделены в отдельный класс – «атомные и ядерные константы» . Следует отметить, что их количество уже намного превышает количество всех других констант вместе взятых . В общей сложности в физике используются уже сотни физических констант. Список фундаментальных физических констант рекомендованный CODATA 1998 насчитывает около 300 фундаментальных физических констант . То, что количество констант достигло уже нескольких сотен, и все они фундаментальные – явно ненормально. Если к ним подходить как к истинно фундаментальным, то их слишком много. Если исходить из того, что в основе мира лежит единая сущность, и что механические, электрические и гравитационные явления должны иметь единую природу, то для описания всех физических явлений и законов не нужно такое большое количество констант. Если же подходить к понятию фундаментальности по полной мере, то истинной фундаментальностью должны обладать совсем минимальное количество констант, а никак не сотни. Таким образом, существует большое противоречие между минимально необходимым количеством фундаментальных констант и их реальным обилием.

Можно предположить, что известные на сегодня константы являются составными константами и статус фундаментальных они носят лишь в силу исторических особенностей их появления. Тогда возникают вопросы: «из каких новых неприводимых констант они могут состоять и как они связаны между собой?». Если такие первичные константы существуют, то они могли бы претендовать на роль фундаментальных физических суперконстант и заменить собой существующие константы. Существуют ли такие суперконстанты, которые в состоянии заменить такое большое количество столь различных фундаментальных физических констант и сколько их? На эти вопросы в рамках современных знаний ответов пока нет.

Наиболее важные современные физические теории оперируют константами G, h, c в их различных комбинациях . Так, например, теорию тяготения Ньютона можно условно назвать G-теорией . Общая теория относительности является классической (G, c)-теорией. Релятивистская квантовая теория поля является квантовой (h, c)-теорией . Каждая из этих теорий оперирует одной или двумя размерными константами. Открытие планковских единиц длины, массы и времени породили надежду на возможность создания новой квантовой теории на основе трех констант. Однако, попытки создать единую теорию электромагнитных полей, частиц и гравитации на основе трех размерных констант – (G, c, h)-теорию, окончились неудачей. Такой теории до сих пор нет, хотя на ее появление возлагали большие надежды . На G—c—h-базис все еще возлагают надежды как на основополагающую тройку констант для будущей теории. И действительно, многое указывает на то, что трех размерных констант должно быть достаточно для создания единой теории. Ведь неспроста только из трех основных единиц – метра, килограмма и секунды можно получить все производные единицы, имеющие механическую природу. Однако до сих пор неясно, какие три константы должны составить основу будущей непротиворечивой теории? Задача эта оказалась очень сложной. Я считаю, что причины сложности кроются в невыясненной сущности многих фундаментальных констант и в невыясненных истоках их происхождения. Проведенные исследования позволяют сказать, что минимальное количество первичных констант, из которых состоят современные фундаментальные физические константы, действительно существует. При этом в минимальный константный базис входят как уже известные физические постоянные, так и новые константы.

Обзор

Слово «постоянная» в физике употребляется в двояком смысле:

• численное значение некоторой величины вообще не зависит от каких-либо внешних параметров и не меняется со временем,
• изменение численного значения некоторой величины несущественно для рассматриваемой задачи.

Например, гелиоцентрическая постоянная, равная произведению гравитационной постоянной на массу Солнца, уменьшается из-за уменьшения массы Солнца, происходящего вследствие излучения им энергии и испускания солнечного ветра. Однако, поскольку относительное уменьшение массы Солнца составляет величину порядка 10-14, то для большинства задач небесной механики гелиоцентрическая постоянная с удовлетворительной точностью может рассматриваться как постоянная. Также в физике высоких энергий постоянная тонкой структуры, характеризующая интенсивность электромагнитного взаимодействия, растёт с ростом переданного импульса (на малых расстояниях), однако её изменение несущественно для широкого круга обычных явлений, например, для спектроскопии.

Физические постоянные делятся на две основные группы — размерные и безразмерные постоянные. Численные значения размерных постоянных зависят от выбора единиц измерения. Численные значения безразмерных постоянных не зависят от систем единиц и должны определяться чисто математически в рамках единой теории. Среди размерных физических постоянных следует выделять постоянные, которые не образуют между собой безразмерных комбинаций, их максимальное число равно числу основных единиц измерения — это и есть собственно фундаментальные физические постоянные (скорость света, постоянная Планка и др.). Все остальные размерные физические постоянные сводятся к комбинациям безразмерных постоянных и фундаментальных размерных постоянных. С точки зрения фундаментальных постоянных, эволюция физической картины мира — это переход от физики без фундаментальных постоянных (классическая физика) к физике с фундаментальными постоянными (современная физика). Классическая физика при этом сохраняет своё значение как предельный случай современной физики, когда характерные параметры исследуемых явлений далеки от фундаментальных постоянных.

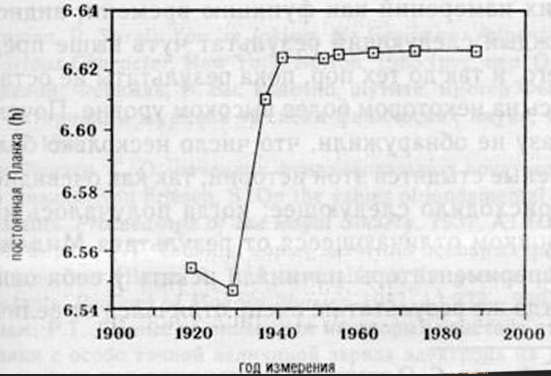
Скорость света появилась ещё в классической физике в XVII в., но тогда она не играла фундаментальной роли. Фундаментальный статус скорость света приобрела после создания электродинамики Дж. К. Максвеллом и специальной теории относительности А. Эйнштейном (1905). После создания квантовой механики (1926) фундаментальный статус приобрела постоянная Планка h, введённая М. Планком в 1901 г. как размерный коэффициент в законе теплового излучения. К фундаментальным постоянным также ряд учёных относит гравитационную постоянную G, постоянную Больцмана k, элементарный заряд e (или постоянную тонкой структуры α) и космологическую постоянную Λ. Фундаментальные физические постоянные являются естественными масштабами физических величин, переход к ним в качестве единиц измерения лежит в основе построения естественной (планковской) системы единиц. К фундаментальным постоянным в силу исторической традиции также относят и некоторые другие физические постоянные, связанные с конкретными телами (например, массы элементарных частиц), однако эти постоянные должны, согласно современным представлениям, каким-то пока неизвестным образом выводиться из более фундаментального масштаба массы (энергии), так называемого вакуумного среднего поля Хиггса.

Международно принятый набор значений фундаментальных физических постоянных и коэффициентов для их перевода регулярно издаётся Рабочей группой CODATA по фундаментальным постоянным.

Boeing YAL-1

Самолет, который должен был сбивать противника лазером. /Фото: medium.com

Boeing YAL-1 — это концепт экспериментального боевого самолёта, которых должен был уничтожать вражеские объекты, в том числе баллистические ракеты, используя мощный химический (бортовой) лазер. Первые упоминания о подобной программе датируются еще концом восьмидесятых, однако первые реальные результаты были получены в 2002 году, когда был собран, оставшийся единственным, опытный образец самолета с необычной возможностью уничтожения вражеского оружия и техники.

Главным плюсом данной системы была возможность ликвидации стартующих баллистических и крылатых ракет с ядерной боевой частью еще на начальном участке траектории полета. Однако даже эта многообещающая технология оказалась беззащитна перед банальным сокращением военного бюджета США. Именно по этой причине в 2001 году проект был закрыт, а еще три года спустя единственный образец Boeing YAL-1 утилизировали.

Скобки

В круглых скобках указывается одна или несколько переменных, от которых зависит физическая величина. Например, f(x,y){\displaystyle f(x,y)} означает, что некоторая величина является функцией (f{\displaystyle f}) величин x{\displaystyle x} и y{\displaystyle y}.

Символ	Значение
u,v{\displaystyle }	векторное произведение, коммутатор между двумя операторами, скобка Паерлза
(u,v){\displaystyle (\mathbf {u} ,\mathbf {v} )}	скалярное произведение
⟨n|A^|m⟩{\displaystyle \langle n|{\hat {A}}|m\rangle }, ⟨u⟩{\displaystyle \langle u\rangle }	бра и кет нотация, средняя величина
{u,v}{\displaystyle \{u,v\}}	скобки Пуассона
|u|{\displaystyle |u|}	модуль
‖u‖{\displaystyle \|u\|}	норма

XM29 OICW

Футуристическая винтовка, так и не вышедшая в серию. /Фото: wikiрedia.org

В девяностых годах прошлого века две компании — американской Alliant Techsystems и немецкой Heckler & Koch — начали разработку совместной программы по созданию принципиально нового вида оружия, построенного по модульной схеме: в результате должна была получиться наполовину винтовка со стандартными пулями 5.56 мм, наполовину гранатомёт калибра 20 мм с боезапасом осколочного боеприпаса дистанционного (воздушного) подрыва.

Примерно в 1999 году необычный концепт обрел материальную форму в виде модели XM29 OICW. При многообещающих технических характеристиках внешний вид оружия оказался соответствующим — неоднократно отмечалось, что оно похоже на футуристическую «пушку» из видеоигр. Однако на деле концепт не оправдал ожидания заказчиков, оказавшись малоэффективным: неудовлетворительное поражающее действие гранаты, а также «неприемлемая масса» самого оружия поставило точку в его дальнейшей разработке, и проект был закрыт в 2004 году.

Специальные символы

Символ	Значение
≪	намного меньше
≫	намного больше
∼	равно по порядку величины
∝	пропорционально
∇{\displaystyle \nabla }	оператор Гамильтона
∇⋅{\displaystyle \nabla \cdot }	дивергенция
∇×{\displaystyle \nabla \times }	ротор
{\displaystyle \square }	даламбертиан
×{\displaystyle \times }	векторное произведение
⊗{\displaystyle \otimes }	тензорное произведение
∂{\displaystyle \partial }	частная производная
ℏ{\displaystyle \hbar }	приведённая постоянная Планка
!	факториал
A{\displaystyle A\!\!\!/}	слэш-обозначения Фейнмана
∧{\displaystyle \wedge }	внешнее произведение
∫ab{\displaystyle \int _{a}^{b}}	интеграл от a до b
∮C{\displaystyle \oint _{C}}	интеграл по контуру
Ø	диаметр

Некоторые избранные постоянные

Использованные сокращения: И — иррациональное число, А — алгебраическое число, Т — трансцендентное число, ? — неизвестно; мат — обычная математика, ТЧ — теория чисел, ТХ — теория хаоса, комб — комбинаторика, АИТ — алгоритмическая теория информации.

Символ	Приближенное значение	Название	Область	Значение	Впервые описана	Число известных знаков
π{\displaystyle \pi }	≈ 3,141 592 653 589 793 238 462 643 383 279 502 88	пи, архимедова константа	мат	Т	до 2600 до н. э. (Месопотамия, Египет)	12 100 000 000 000
τ{\displaystyle \tau }	≈ 6,283 185 307 179 586	тау (2π)	мат	Т
e	≈ 2,718 281 828 459 045 235 360 287 471 352 662 50	константа Непера, число Эйлера, основание натурального логарифма	мат	Т	1618	12 884 901 000
2{\displaystyle {\sqrt {2}}}	≈ 1,414 213 562 373 095 048 801 688 724 209 698 08	константа Пифагора, квадратный корень из 2	мат	А, И	до 1800 до н. э.	137 438 953 444
3{\displaystyle {\sqrt {3}}}	≈ 1,732 050 807 568 877 293 527 446 341 505 872 37	константа Феодора, квадратный корень из 3	мат	А, И	до 800 до н. э.
γ	≈ 0,577 215 664 901 532 860 606 512 090 082 402 43	постоянная Эйлера — Маскерони	мат, ТЧ	?	1735	108 000 000
φ	≈ 1,618 033 988 749 894 848 204 586 834 365 638 12	золотое сечение	мат	А, И	ок. 300 до н. э.	3 141 000 000
β*	≈ 0,702 58	константа Эмбри — Трефетена	ТЧ
δ	≈ 4,669 201 609 102 990 671 853 203 820 466 201 61	постоянная Фейгенбаума	ТХ		1975
α	≈ 2,502 907 875 095 892 822 283 902 873 218 215 78	константа Фейгенбаума	ТХ		1975
C2	≈ 0,643 410 546 29	Константа Каэна	ТЧ	Т
C2	≈ 0,660 161 815 846 869 573 927 812 110 014 555 77	константа простых близнецов	ТЧ			5 020
M1	≈ 0,261 497 212 847 642 783 755 426 838 608 695 85	константа Майсселя — Мертенса	ТЧ		;	8010
B2	≈ 1,902 160 583 104	константа Бруна для простых близнецов	ТЧ			10
B4	≈ 0,870 588 380 0	константа Бруна для простых четвёрок	ТЧ
	≈ 0,662 743 419 349 181 580 974 742 097 109 252 90	предел Лапласа	мат
G	≈ 0,915 965 594 177 219 015 054 603 514 932 384 11	постоянная Каталана	комб			31 026 000 000
Λ	Λ ≥ 0	константа де Брёйна — Ньюмана	ТЧ		,
K	≈ 0,764 223 653 589 220 66	константа Ландау — Рамануджана	ТЧ	И (?)		30 010
K	≈ 1,131 988 24	константа Висваната	ТЧ			16
K	≈ 2,685 452 001 065	постоянная Хинчина	ТЧ
J	≈ 3,058 198 247 456 354 132 564 564 787 888 767…	константа Поля — Гаусса	ТЧ			10343
B´L	1 (первоначальная гипотеза 1,08366)	константа Лежандра	ТЧ	Ц		точное значение
λ	≈ 0,624 329 988 543 550 870 992 936	Постоянная Голомба — Дикмана	ТЧ
μ	≈ 1,451 369 234 883 381 050 283 968 485 892 027	константа Рамануджана — Солднера	ТЧ			75 500
E’B	≈ 1,606 695 152 415 291 763	константа Эрдёша — Борвейна	ТЧ	И
Ω	≈ 0,007 874 996 997 812 384 4	константа Хайтина	АИТ	Т
ζ(3)	≈ 1,202 056 903 159 594 285 399 738 161 511 449 99	постоянная Апери	ТЧ	И		100 000 001 000
ɯ	≈ 0,739 085 133 215 160 641 655 312 087 673 873 40	число Дотти, притягивающая неподвижная точка функции cos(x)	ТХ
A	≈ 1,282 427 129 100 622 636 875 342 568 869 791 73	постоянная Глейшера — Кинкелина	ТЧ
θ, A	≈ 1,306 377 883 863 080 690 468 614 492 6	Константа Миллса	ТЧ			6850
ρ	≈ 1,324 717 957 244 746 025 960 908 854 478	Пластическое число	ТЧ	А, И

«Gyrojet»

Не самый удачный бесшумный пистолет. /Фото: alloutdoor.com

В начале 1960-х годов компания MB Associates дала начало появлению целого семейства уникальных ракетных пистолетов и винтовок. В сущности, эти модели оружия были не такими плохими: они имели удовлетворительную эффективность, к тому же являлись бесшумными.

Однако их история не была успешной, и, пожалуй, главным их достижением оказалось появление в киноленте про легендарного агента 007 Джеймса Бонда «Живёшь только дважды». Ведь практика его использования показала, что за пределами экрана оружие было недостаточно точным, малополезные снаряды при использовании на ближних дистанциях, к тому же часто допускало осечки.

Атомная и ядерная физика

Энергия кванта электромагнитной волны (в т.ч. света) или, другими словами, энергия фотона вычисляется по формуле:

Импульс фотона:

Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ):

Максимальная кинетическая энергия вылетающих электронов при фотоэффекте может быть выражена через величину задерживающего напряжение U_з и элементарный заряд е:

Существует граничная частота или длинна волны света (называемая красной границей фотоэффекта) такая, что свет с меньшей частотой или большей длиной волны не может вызвать фотоэффект. Эти значения связаны с величиной работы выхода следующим соотношением:

Второй постулат Бора или правило частот (ЗСЭ):

В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах:

На любой орбите в атоме водорода кинетическая (К) и потенциальная (П) энергии электрона связаны с полной энергией (Е) следующими формулами:

Общее число нуклонов в ядре равно сумме числа протонов и нейтронов:

Дефект массы:

Энергия связи ядра выраженная в единицах СИ:

Энергия связи ядра выраженная в МэВ (где масса берется в атомных единицах):

Формула альфа-распада:

Формула бета-распада:

Закон радиоактивного распада:

Ядерные реакции

Для произвольной ядерной реакции описывающейся формулой вида:

Выполняются следующие условия:

Энергетический выход такой ядерной реакции при этом равен: