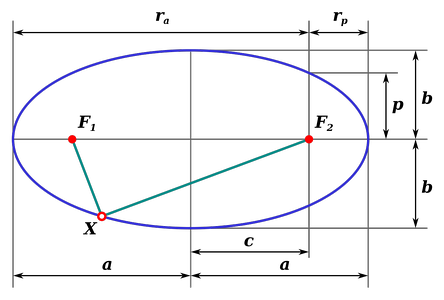
Постоянная тонкой структуры

Ссылки Править

• Cohen E.R., Crowe C.M., Dumond J.W.M. Fundamental constants of physics. N.Y., L., 1957, 287 p.
• Barrow J.D. The Constants of Nature: From Alpha to Omega. London: Jonathan Cape, 2002. N.Y.: Pantheon, 2003, 353 p.
• Спиридонов О. П. Фундаментальные физические постоянные. М.: Высшая школа, 1991, 238 с.
• Сагитов М. У. Постоянная тяготения и масса Земли. М.: Наука, 1969, 188 с.
• Квантовая метрология и фундаментальные константы. М.: Мир, 1981, 368 с.

• Страница — краткая статья
• Страница — энциклопедическая статья
• Разное — на страницах: , , ,

Объяснение тонкой структуры спектра

Развитие представлений о постоянной тонкой структуры связано с дальнейшим прогрессом квантовой физики, в частности с понятием спина – собственного момента импульса частицы. Выяснилось, что тонкое расщепление спектральных линий обусловлено не только релятивистским движением электрона в атоме, но и взаимодействием его спинового момента с орбитальным. В зависимости от ориентации спина оно может описываться как векторной суммой, так и разностью, в результате чего и возникают малые различия в значениях энергии, приводящие к расщеплению линии в спектре.

Что касается константы «альфа», то она (точнее ее квадрат) входит в качестве коэффициента в уравнение спин-орбитального взаимодействия, дающего поправку к энергии атомного электрона. Иными словами, эта постоянная определяет размер тонкого расщепления линий спектра. Однако это мало проясняет ее физическую природу.

Скорость света в вакууме

В соответствии с теорией относительности Эйнштейна скорость света в вакууме  является абсолютной константой. Большинство современных физических теорий основывается именно на этом постулате. Поэтому существует стойкое теоретическое предубеждение против того, чтобы рассматривать вопрос о возможном изменении скорости света в вакууме. В любом случае вопрос этот в настоящее время официально признан закрытым. С 1972 г. скорость света в вакууме была объявлена постоянной по определению и теперь считается равной 299792,458 ± 0,0012 к/с.

Так же как и в случае с гравитационной постоянной, прежние измерения этой константы значительно отличались от современной, официально признанной величины. К примеру, в 1676 г. Ремер вывел величину, которая была на 30 % ниже современной, а полученные в 1849 г. результаты Физо были на 5 % выше.

С 1928 по 1945 гг. скорость света в вакууме, как оказалось, была на 20 км/с меньше, чем до и после этого периода.

В конце 40-х гг. величина этой константы вновь стала возрастать. Неудивительно, что когда новые измерения стали давать более высокие значения этой постоянной, среди ученых сначала возникло некоторое недоумение. Новая величина оказалась примерно на 20 км/с выше прежней, то есть достаточно близкой к установленной в 1927 г. Начиная с 1950 г. результаты всех измерений этой константы опять оказались очень близки друг к другу (ил. 15). Остается лишь предполагать, как долго сохранялось бы единообразие получаемых результатов, если бы измерения продолжали проводиться. Но на практике в 1972 г. было принято официальное значение скорости света в вакууме, а дальнейшие исследования прекращены.

В экспериментах проведённых доктором наук Люжин Ванг (Dr. Lijun Wang) в NEC исследовательском институте в Принстоне (NEC research institute in Princeton), были получены удивительные результаты. Эксперимент заключался в том, что световые импульсы пропускались через ёмкость, наполненную специально обработанным газом цезия. Результаты экспериментов оказались феноменальными — скорость световых импульсов оказалась в 300 (триста) раз больше, чем допустимая скорость из преобразований Лоренца (2000 год)!

В Италии, другая группа физиков из Итальянского Национального Совета по исследованиям (Italian National Research Council), в своих экспериментах с микроволнами (2000 год) получила скорость распространения их на 25% больше, чем допустимая скорость по А. Эйнштейну…

Самое интересно, что Эйншейну было известно о непостоянстве скорости света:

Постоянная Планка

Постоянная Планка (h) является фундаментальной константой квантовой физики и связывает частоту излучения (υ) с квантом энергии (Е) в соответствии с формулой E-hυ. Она имеет размерность действия (то есть произведения энергии на время).

Нам твердят, что квантовая теория — образец блестящего успеха и удивительной точности: «Законы, открытые при описании квантового мира (…) являются наиболее верными и точными инструментами из всех, когда-либо применявшихся для успешного описания и предсказания Природы. В некоторых случаях совпадение между теоретическим прогнозом и реально полученным результатом настолько точно, что расхождения не превышают одной миллиардной части».

Подобные утверждения я слышал и читал так часто, что привык считать, будто численное значение постоянной Планка должно быть известно с точностью до самого дальнего знака после запятой. Кажется, что так оно есть: стоит лишь заглянуть в какой-нибудь справочник по этой теме. Однако иллюзия точности исчезнет, если открыть предыдущее издание того же справочника. На протяжении многих лет официально признанная величина этой «фундаментальной константы» изменялась, демонстрируя тенденцию к постепенному возрастанию.

Максимальное изменение значения постоянной Планка отмечалось с 1929 по 1941 гг., когда ее величина возросла более чем на 1 %. В значительной степени это увеличение было вызвано существенным изменением экспериментально измеренного заряда электрона, е. Измерения постоянной Планка не дают непосредственных значений данной константы, поскольку при ее определении необходимо знать величину заряда и массу электрона. Если одна или тем более обе последние константы изменяют свои величины, изменяется и величина постоянной Планка.

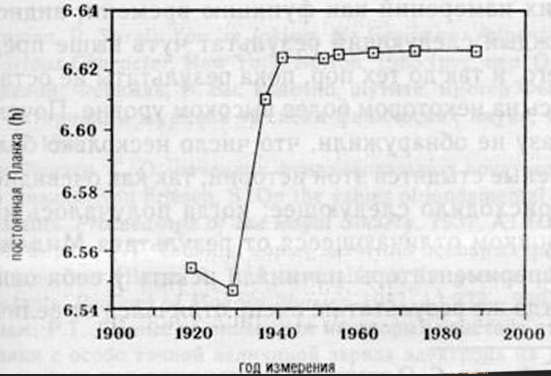
Изменение постоянной Планка с течением времени

Гравитационная постоянная

Гравитационная постоянная (G) впервые появилась в выведенном Ньютоном уравнении силы тяжести, в соответствии с которым сила гравитационного взаимодействия двух тел равна отношению умноженного на нее произведения масс этих взаимодействующих тел к квадрату расстояния между ними. Значение этой константы многократно измерялось с тех пор, как в 1798 г. было впервые определено в точном эксперименте Генри Кавендишем.

В начальной стадии измерений наблюдался значительный разброс результатов, а затем прослеживается хорошая сходимость получаемых данных. Тем не менее даже после 1970 г. «лучшие» результаты колеблются в диапазоне от 6,6699 до 6,6745, то есть разброс составляет 0,07 %.

Из всех известных фундаментальных констант именно численное значение гравитационной постоянной определено с наименьшей точностью, хотя важность этой величины трудно переоценить. Все попытки прояснить точное значение этой константы не увенчались успехом, а все измерения так и остались в слишком большом диапазоне возможных значений

Тот факт, что точность численного значения гравитационной постоянной до сих пор не превышает 1/5000, редактор журнала «Nature» определил как «пятно позора на лице физики».

В начале 80-х гг. Фрэнк Стейси со своими коллегами измерял эту константу в глубоких шахтах и скважинах Австралии, и полученное им значение оказалось примерно на 1 % выше официального значения, принятого в настоящее время. 

Физическая сущность явления

Универсальная динамическая проводимость графена

В общем случае действительная часть динамической проводимости в графене определяется следующим образом:

GR=πe2ωv(ω)2D(ω)f(−ℏω2)−f(ℏω2), {\displaystyle G_{R}={\frac {\pi e^{2}}{\omega }}v(\omega )^{2}D(\omega ),\ }

где v(ω){\displaystyle v(\omega )} — скорость матричных элементов между начальной энергией фотона −ℏω2 {\displaystyle -{\frac {\hbar \omega }{2}}\ } и конечной ℏω2 {\displaystyle {\frac {\hbar \omega }{2}}\ }, D(ω){\displaystyle D(\omega )} — плотность состояний в графене, f(E)=1exp⁡(ET)+1{\displaystyle f(E)={\frac {1}{\exp(E/T)+1}}} — статистическое распределение Ферми — Дирака, E{\displaystyle E} — энергия, T{\displaystyle T} — температура и ω{\displaystyle \omega } — частота падающих фотонов.

Безусловно, это достаточно сложное выражение, которое плохо поддаётся теоретическому расчету в общем случае. Но для графена можно сделать следующие упрощения:

D(ω)≈ℏωt2a2, {\displaystyle D(\omega )\approx {\frac {\hbar \omega }{t^{2}a^{2}}},\ }

где t{\displaystyle t} — энергия перескоков (около 3 эВ) и a{\displaystyle a} — межатомное расстояние (около 1,42 ангстрем).

v(ω)≈vF≈taℏ, {\displaystyle v(\omega )\approx v_{F}\approx {\frac {ta}{\hbar }},\ }

где vF{\displaystyle v_{F}} — скорость Ферми в графене.

Для произведения «прыжкового импульса» на межатомное расстояние можно взять оценку из соотношения неопределённостей:

ta≈,5h. {\displaystyle ta\approx 0,5h.\ }

Таким образом, предельное масштабное значение для универсальной динамической проводимости будет определяться только через фундаментальные постоянные:

G=e24ℏ. {\displaystyle G_{0}={\frac {e^{2}}{4\hbar }}.\ }

Данное значение и было подтверждено в опытах Кузьменко в диапазоне энергий падающих фотонов от 0,1 до 0,2 эВ.

Оптическая проницаемость графена

Ещё в работе Кузьменко отмечалось, что коэффициент пропускания оптического излучения одноатомным слоем графена может быть представлен в виде:

Topt=1(1+2πGc)2=1(1+,5πα)2≈,977,{\displaystyle T_{opt}={\frac {1}{(1+{\frac {2\pi G_{0}}{c}})^{2}}}={\frac {1}{(1+0,5\pi \alpha )^{2}}}\approx 0,977,}

где c− {\displaystyle c-\ } скорость света. Таким образом, коэффициент пропускания полностью определяется безразмерными фундаментальными величинами.

В общем случае наличия нескольких слоёв графена (бинарный и выше), мы будем иметь коэффициент поглощения:

1−Tn≈nπα, {\displaystyle 1-T_{n}\approx n\pi \alpha ,\ }

где n=1,2,3,…{\displaystyle n=1,2,3,…} — число одноатомных слоёв графена в образце.
Для наглядности Нэйр использовал в своих образцах плавный переход от одноатомного к бинарному слоям графена и с точностью до нескольких процентов подтвердил указанную теорию.

«Тэйлситтеры»

Один из первых самолетов вертикального взлета. /Фото: popmech.ru

Пожалуй, концепция вертикально взлетающего летательного аппарата появилась едва ли не с начала эпохи авиации, однако попытки воплотить ее в жизнь были предприняты гораздо позже. Так, одна из первых разработок, призванных удовлетворить данный запрос, был открыт к середине прошлого века.

Проект по созданию так называемых «Тэйлситтеров» был начат в 1950 году, а представлял собой одну из первых вариантов самолетов, «сидящих на хвосте», то есть таких, которые взлетали бы вертикально. Казалось бы, что успешно отстроенные опытные образцы обеспечат успешный исход испытаний, однако на деле все случилось иначе

Выяснилось, что взлёт и приземление самолетов данного типа требовали от летчиков большой осторожности и мастерства. Угроза жизни управлении и стали причиной закрытия проекта, хотя основные составляющие концепта тэйлситтеров в дальнейшем использовались при создании летающих дронов

Связь спин-орбита

Поправка спин-орбита появляется, когда мы из стандартной системы отсчёта (где электрон облетает вокруг ядра) переходим в систему, где электрон покоится, а ядро облетает вокруг него. В этом случае движущееся ядро представляет собой эффективную петлю с током, которая в свою очередь создаёт магнитное поле. Однако электрон сам по себе имеет магнитный момент из-за спина. Два магнитных вектора, B→{\displaystyle {\vec {B}}} и μ→s{\displaystyle {\vec {\mu }}_{s}} сцепляются вместе так, что появляется определённая энергия, зависящая от их относительной ориентации. Так появляется энергетическая поправка вида
ΔESO=ξ(r)L→⋅S→{\displaystyle \Delta E_{SO}=\xi (r){\vec {L}}\cdot {\vec {S}}}

Наземные боевые роботы

Неудачная попытка создать боевого робота. /Фото: popmech.ru

Когда в конце 1990-х — первой половине 2000-х годов беспилотные летательные аппараты доказали свою эффективность во время военных конфликтов на Среднем Востоке, они стали одним из основных типов оружия армии США. В свою очередь наземные роботы в большинстве остались на периферии.

Переломить ситуацию решили в 2007 году во время боевых действий в Ираке. Туда были отправлены наземные боевые роботы, представленные модифицированными для стрельбы роботами TALON. Однако их история закончилась не начавшись, и в реальных полевых условиях в пекле войны они так и не побывали. А все потому, что они откровенно провалили испытания, во время которых над ними было потеряно управление, и роботы попросту вышли из строя.

Что такое константа?

Фундаментальные физические постоянные или как их еще часто называют константы являются неотъемлемой частью современной науки, и незаменимы при решении задач. Но что такое константа? Давайте разберемся по порядку.

Все объекты, тела процессы и явления в этом мире обладают различными характеристиками. К примеру, говоря что человек высокий, мы рассматриваем такую его характеристику как рост, а рассказывая друзьям о том что наш мопед способен разгоняться до 65 км/ч, (правда с горки, да и то когда ветер в спину), рассматривается максимальная скорость мопеда. И понятно что люди бывают высокие и низкие, а максимальная скорость мопедов может очень сильно варьироваться, но существуют такие величины и характеристики которые остаются неизменными. Их называют константами или постоянными

К примеру известно что все тела будут падать на землю с одинаковым ускорением, и неважно слон это или ваш любимый кот, ускорение будет равно примерно 9.8 м/с2. И это будет константа

Константа — величина, не меняющая своё значение в рамках рассматриваемого процесса

Стоит отметить что физические постоянные не всегда являются характеристиками того или иного объекта или явления, а могут быть просто коэффициентом пропорциональности для перевода вычислений в единую систему единиц. (Чаще всего СИ). По мимо этого при решении физических задач пригодятся и некоторые математические константы, например число π. Но нас в первую очередь интересуют физические постоянные по этому рассмотрим основные из них:

«Алмазная галька»

Сеть противоракетных спутников с поэтичным названием. /Фото: trinixy.ru

Программа «Алмазная галька» (в других переводах — «Бриллиантовая галька») разрабатывалась в рамках так называемой Стратегической Оборонной Инициативы (сокр. СОИ, также «звездные войны»), которая, в свою очередь, представляла собой глобальную противоракетную сеть США в период Холодной войны. Ее начало объявил президент Рональд Рейган 23 марта 1983 года, а состояла она как из научно-исследовательской деятельности в данном направлении, так и опытно-конструкторских проектных работ.

Согласно сохранившимся свидетельствам, программа «Алмазная галька» была предложена в 1986 году и предусматривала создание сети из 4000 военных кинетических спутников-перехватчиков, которые должны были сбивать советские ракеты с помощью с помощью кинетического удара при прямом столкновении. Именно данная система считалась наиболее перспективной среди ряда других разработок программы СОИ, однако это не обеспечило ей достойного будущего, которое разбилось об исторический контекст. Проект не был реализован в конце 1980-х, а после развала СССР в нем уже не было необходимости, и его закрыли в 1994 году.

Релятивистские поправки

В классической теории кинетический член гамильтониана:
T=p22m{\displaystyle T={\frac {p^{2}}{2m}}}

Однако, учитывая СТО, мы должны использовать релятивистское выражение для кинетической энергии,
T=p2c2+m2c4−mc2{\displaystyle T={\sqrt {p^{2}c^{2}+m^{2}c^{4}}}-mc^{2}}

где первый член — это общая релятивистская энергия, а второй член — это энергия покоя электрона. Раскладывая это в ряд, получаем

T=p22m−p48m3c2+…{\displaystyle T={\frac {p^{2}}{2m}}-{\frac {p^{4}}{8m^{3}c^{2}}}+\dots }

Отсюда, поправка первого порядка к гамильтониану равна
H′=−p48m3c2{\displaystyle H’=-{\frac {p^{4}}{8m^{3}c^{2}}}}

Используя это как возмущение, мы можем вычислить релятивистские энергетические поправки первого порядка.

En(1)=⟨ψ|H′|ψ⟩=−18m3c2⟨ψ|p4|ψ⟩=−18m3c2⟨ψ|p2p2|ψ⟩{\displaystyle E_{n}^{(1)}=\langle \psi ^{0}\vert H’\vert \psi ^{0}\rangle =-{\frac {1}{8m^{3}c^{2}}}\langle \psi ^{0}\vert p^{4}\vert \psi ^{0}\rangle =-{\frac {1}{8m^{3}c^{2}}}\langle \psi ^{0}\vert p^{2}p^{2}\vert \psi ^{0}\rangle }

где ψ{\displaystyle \psi ^{0}} — невозмущенная волновая функция. Вспоминая невозмущенный гамильтониан, мы видим

H|ψ⟩=En|ψ⟩{\displaystyle H^{0}\vert \psi ^{0}\rangle =E_{n}\vert \psi ^{0}\rangle }

(p22m+U)|ψ⟩=En|ψ⟩{\displaystyle \left({\frac {p^{2}}{2m}}+U\right)\vert \psi ^{0}\rangle =E_{n}\vert \psi ^{0}\rangle }

p2|ψ⟩=2m(En−U)|ψ⟩{\displaystyle p^{2}\vert \psi ^{0}\rangle =2m(E_{n}-U)\vert \psi ^{0}\rangle }

Далее, мы можем использовать этот результат для вычисления релятивистской поправки:

En(1)=−18m3c2⟨ψ|p2p2|ψ⟩{\displaystyle E_{n}^{(1)}=-{\frac {1}{8m^{3}c^{2}}}\langle \psi ^{0}\vert p^{2}p^{2}\vert \psi ^{0}\rangle }

En(1)=−18m3c2⟨ψ|(2m)2(En−U)2|ψ⟩{\displaystyle E_{n}^{(1)}=-{\frac {1}{8m^{3}c^{2}}}\langle \psi ^{0}\vert (2m)^{2}(E_{n}-U)^{2}\vert \psi ^{0}\rangle }

En(1)=−12mc2(En2−2En⟨U⟩+⟨U2⟩){\displaystyle E_{n}^{(1)}=-{\frac {1}{2mc^{2}}}(E_{n}^{2}-2E_{n}\langle U\rangle +\langle U^{2}\rangle )}

Для атома водорода, U=e2r{\displaystyle U={\frac {e^{2}}{r}}}, ⟨U⟩=e2an2{\displaystyle \langle U\rangle ={\frac {e^{2}}{a_{0}n^{2}}}} и ⟨U2⟩=e4(l+12)n3a2{\displaystyle \langle U^{2}\rangle ={\frac {e^{4}}{(l+1/2)n^{3}a_{0}^{2}}}} где a{\displaystyle a_{0}} — боровский радиус, n{\displaystyle n} — главное квантовое число и l{\displaystyle l} — орбитальное квантовое число. Следовательно, релятивистская поправка для атома водорода равна

En(1)=−12mc2(En2−2Ene2an2+e4(l+12)n3a2)=−En22mc2(4nl+12−3){\displaystyle E_{n}^{(1)}=-{\frac {1}{2mc^{2}}}\left(E_{n}^{2}-2E_{n}{\frac {e^{2}}{a_{0}n^{2}}}+{\frac {e^{4}}{(l+1/2)n^{3}a_{0}^{2}}}\right)=-{\frac {E_{n}^{2}}{2mc^{2}}}\left({\frac {4n}{l+1/2}}-3\right)}