Чему равна гравитационная постоянная?
Содержание:
- Сравнение силы тяготения на Земле с другими небесными телами
- Происхождение Луны
- Тепловая машина
- Трудности с низкой гравитацией
- Квантово-релятивистская формулировка гравитационной постоянной[править]
- Рождение планет
- Saturday Morning Science
- Лунотрясения
- Лунные аномалии
- Особенности гравитации
- Аномальная гравитация на Луне
- Из истории гравитационной постоянной
- Примечания[править | править код]
- Эффект Пельтье, Томсон и температура
- Примечания[править]
- Притяжение Луны и Земли
- Вывод гравитационной константы «Метод G-2001» и массы Солнца, Земли, Луны.
Сравнение силы тяготения на Земле с другими небесными телами
В таблице приведены значения величин ускорения свободного падения на поверхности Земли, Солнца, Луны, планет Солнечной системы, ряда спутников и астероидов. Для планет — гигантов под «поверхностью» понимается видимая поверхность, а для Солнца — верхняя граница фотосферы. Данные в таблице не учитывают эффекта центробежной силы от вращения планет и фактически означают значения искомых величин вблизи полюсов планет. Справочно указано время падения объекта на данное небесное тело со 100-метровой высоты и максимальная скорость, достигаемая при этом (сопротивление воздуха не учтено).
| Небесное тело | Сила тяжестипо сравнению с земной | Ускорение свободного падения на поверхности, м/с2 | Примечания | Время падения со 100-метровой высоты/Достигаемая при этом скорость | |
|---|---|---|---|---|---|
| Солнце | 27,90 | 274,1 | 0,85 сек | 843 км/ч | |
| Меркурий | 0,3770 | 3,7 | 7,4 сек | 98 км/ч | |
| Венера | 0,905 | 8,872 | 4,8 сек | 152 км/ч | |
| Земля | 1 | 9,80665 | 4,5 сек | 159 км/ч | |
| Луна | 0,1657 | 1,625 | 11,1 сек | 65 км/ч | |
| Марс | 0,3795 | 3,728 | 7,3 сек | 98 км/ч | |
| Церера | 0,029 | 0,028 | 26,7 сек | 27 км/ч | |
| Юпитер | 2,640 | 25,93 | 2,8 сек | 259 км/ч | |
| Ио | 0,182 | 1,789 | 10,6 сек | 68 км/ч | |
| Европа | 0,134 | 1,314 | 12,3 сек | 58 км/ч | |
| Ганимед | 0,145 | 1.426 | 11,8 сек | 61 км/ч | |
| Каллисто | 0,126 | 1,24 | 12,7 сек | 57 км/ч | |
| Сатурн | 1,139 | 11,19 | 4,2 сек | 170 км/ч | |
| Титан | 0,138 | 1,352 | 12,2 сек | 59 км/ч | |
| Уран | 0,917 | 9,01 | 4,7 сек | 153 км/ч | |
| Титания | 0,039 | 0,379 | 23,0 сек | 31 км/ч | |
| Оберон | 0,035 | 0,347 | 24,0 сек | 30 км/ч | |
| Нептун | 1,148 | 11,28 | 4,2 сек | 171 км/ч | |
| Тритон | 0,079 | 0,779 | 16,0 сек | 45 км/ч | |
| Плутон | 0,063 | 0,62 | 18,1 сек | 40 км/ч | |
| Эрида | 0,0814 | 0,8 | (приблизит.) | 15,8 сек | 46 км/ч |
Происхождение Луны
Откуда взялась Луна? Простого и точного ответа нет, но, тем не менее, наука позволяет сделать несколько предположений.
Есть пять основных теорий о происхождении Луны. Теория деления утверждает, что Луна когда-то была частью нашей планеты и отделилась от неё на очень раннем этапе истории Земли — на самом деле Луна как раз могла бы находиться на месте современного Тихого океана. Теория захвата говорит, что Луна просто «скиталась» по Вселенной, пока не была захвачена земной гравитацией. Другие теории гласят, что наш спутник либо сформировался из обломков астероидов, либо остался от столкновения Земли с неизвестной планетой размером с Марс.
Самая достоверная на данный момент теория происхождения Луны называется Теорией Колец: протопланета (планета, которая только формируется) под названием Тейя столкнулась с Землёй, и образовавшееся после этого облако мусора в конечном итоге собралось вместе и превратилось в Луну.
Тепловая машина

Рис. 3. Кубик Рубика и тепловая машина.
Приведенные на рисунках примеры показывают, что мы фактически создали тепловую машину, работающую по циклу Карно (рис. 3).
В начале процесса кубик имеет комнатную температуру, точка (А). Затем мы его привели в контакт с охладителем (ВС), который изотермически (при постоянной температуре) отнимает от него некоторое количество теплоты. При этом объём кубика уменьшился. Далее мы вынули кубик и нагрели до комнатной температуры (DA). Цикл закончился.
В начале второго цикла кубик привели в контакт с нагревателем (EF) который изотермически передал ему порцию теплоты. Кубик расширился. Закончили цикл, охладив кубик при комнатной температуре (DA).
Если данный кубик заранее соединить, например, с поршнем, то он бы совершил работу. Но что это за работа — хуже вышивания!
Для того чтобы возникло тяготение, направленное по какому либо результирующему вектору, необходимо нарушить тепловое равновесие, либо относительно земли совершить работу по увеличению потенциальной энергии (поднять тело на высоту).
Назад Вперед
Карно Сади (1796-1832) – французский физик и математик
Трудности с низкой гравитацией

Хотя гравитация на Луне равняется только одной шестой от земной гравитации, двигаться по её поверхности — настоящий подвиг. Базз Олдрин говорил, что основать на Луне поселения будет чрезвычайно сложно: ноги астронавтов в громоздких скафандрах утопали в лунной пыли почти на 15 см.
Несмотря на низкую гравитацию, инерция человека на Луне высока, поэтому двигаться быстро или менять направление там сложно. Если астронавты хотели двигаться быстрее, им приходилось изображать из себя неуклюжих кенгуру, что тоже было проблемой, поскольку на Луне полно кратеров и других опасных объектов.
Квантово-релятивистская формулировка гравитационной постоянной[править]
- Основная статья: Естественно-единая квантовая теория взаимодействий
Естественно-единая квантовая теории взаимодействий показала, что константы всех фундаментальных взаимодействий выражаются через постоянную тонкой структуры (ПТС). В этом случае значение \(G\) будет иметь следующий вид
$$G=\sqrt{3}\alpha^{18}\frac{\hbar c}{m_{pa}^{2}},$$
где \(\alpha\) — ПТС,
\(\hbar\) — приведённая постоянная Планка,
\(c\) — скорость света в вакууме,
\(m_{pa}\) — присоединённая масса протона.
Полученная формула раскрывает скрытый квантово-релятивистский статус самого закона тяготения Ньютона. Дело в том, что произведение \(\hbar\times c\), входящее в \(\alpha\) и \(G\), сохраняется только при одновременном преобразовании \(c \rightarrow\infty\) и \(\hbar\rightarrow0\) согласно принципу соответствия. Таким образом, говорить об одностороннем (не квантово-релятивистском) уточнении закона тяготения Ньютона оказывается в принципе неправильно.
На основе данных, приведённых в нижеследующей таблице (взяты из Википедии 07.03.2018), получаем:
$$m_{pa}=1.68082*10^{-27}.$$
Таким образом, значение \(m_{pa}\) всего на 9 электронных масс превышает
массу протона \(m_{p}\) и может считаться достоверным.
| Параметр | Значение |
|---|---|
| \(\hbar\) | 1.054 571 800(13) \(\times 10^{-34}\) Дж c |
| с | 299 792 458 м/с |
| \(\alpha\) | 7.297 352 566 4(17) \(\times 10^{-3} \) |
| G | 6.674 08(31) \(\times10^{-11}\) \(м^{3}\) \(с^{-2}\) \(кг^{-1}\) |
В качестве примера оценки \(m_{pa}\) можно считать, что эта величина включает массу протона \(m_{p}\) и массу электрона \(m_е\). Кроме того необходимо включить массу нейтрона \(m_n\) с коэффициентом \(\delta\) — долей нейтронов на один протон, которая составляет десятые для звёзд и единицы для планет. Также надо вычесть энергию связи связанных нуклонов, которая различна для звёзд и планет. Наконец, надо добавить кинетическую энергию на нуклон и другие возможные вклады. В результате константа \(G\) превратится в константу \(G_{ik}\), где, например, i и k — индексы Солнца и планет.
Таким образом, вместо \(G\) вводится физически осмысленная космологическая константа \(m_{pa}\). Простейшая интерпретация такова: присоединённая масса протона \(m_{pa}\) равна массе протона \(m_{p}\) и массе электрона \(m_{e}\) (т.е. массе атома водорода), причём их суммарная кинетическая энергия равна 4 Mev (масса восьми электронов).
В такой формулировке закон Ньютона говорит нам, что в первом приближении Вселенная в основном состоит из горячего водорода.
Таким образом, закон Ньютона не чувствует тёмную материю и не может быть использован для её обоснования.
Такое же заключение можно сделать и относительно тёмной энергии.
Рождение планет
06/03/2015
Gennadiy Ershov

Рис. 1. Астронавты: командир МКС-06 Kenneth Dwane Bowersox, Бортинженеры: Бударин Н.М. (Россия), Donald Roy Pettit, слева (США)
Saturday Morning Science
Из элементарных, простых частиц рождаются планеты.
Астронавт НАСА Donald Roy Pettit (Дон Петтит), находясь на международной космической станции, посвятил свой выходной день науке. Дон Петтит провел серию простых экспериментов с пищевыми продуктами, заодно и пообедал. Все эксперименты отсняты на видео и выложены в свободном доступе на YouTube .
Много опытов было проведено с водой, с добавлением в нее воздушных пузырьков, красителей и прочих добавок. Но меня больше всего заинтересовали опыты, где обнаруживалось действие гравитации.
Лунотрясения

Несмотря на то, что, по сути, Луна — это просто мёртвый кусок скалы с крайне низкой геологической активностью, движения коры случаются и там. Называются они лунотрясениями (по аналогии с землетрясениями).
Существует четыре вида лунотрясений: первые три — глубокие лунотрясения, колебания от ударов метеоритов и тепловые лунотрясения, вызванные солнечной активностью, — относительно безопасны. А вот лунотрясения четвёртого вида могут быть довольно неприятными. Обычно они составляют до 5,5 баллов по шкале Рихтера — этого достаточно, чтобы начали дрожать небольшие объекты. Длятся такие толчки примерно по десять минут. По данным НАСА, такие лунотрясения заставляют нашу Луну «звенеть, как колокол».
Самое пугающее в этих лунотрясениях то, что у нас нет ни малейшего понятия о том, что именно их вызывает. Землетрясения на Земле, как правило, вызваны движением тектонических плит, но на Луне тектонических плит просто нет. Некоторые исследователи думают, что они могут иметь некоторую связь с приливной активностью Земли, которая как бы «тянет» Луну на себя. Однако теория ничем не подкреплена — приливные силы связаны с полнолуниями, а лунотрясения обычно наблюдаются в другое время.
Лунные аномалии
На некоторых снимках, сделанных различными спутниками, видны очень странные вещи на поверхности Луны. Кажется, что на Луне есть искусственные конструкции, размер которых варьируется от совсем крошечных, обычно имеющих форму параллелепипеда, до «обелисков» не менее 1,5 км высотой.
Любители паранормальных явлений даже «нашли» среди этих объектов большой замок, «висящий» высоко над поверхностью Луны. Всё это как будто указывает на развитую цивилизацию, ранее жившую на Луне и якобы построившую сложные структуры.
НАСА никогда не опровергали эти странные теории, несмотря на то, что все снимки, скорее всего, подделаны приверженцами «теории заговора».
Особенности гравитации
Гравитация непосредственно влияет
на вес объекта, который находится в ее поле. Именно поэтому на разных планетах
тело имеет разную массу. К примеру, если
на Земле человек весит 70 килограмм, то на Плутоне его вес будет около 4,6 кг,
а на Юпитере, наоборот, 170 кг.
Интересные факты о гравитации в
том, что даже на Земле гравитация неоднородная. Это связано с тем, что планета
имеет не идеальную форму шара. Она немного приплюснута. В результате масса
распределяется неравномерно. На полюсах гравитация немного сильнее, чем в
области экватора.
В Канаде в районе Гудзонова залива наблюдается гравитационная аномалия. В этом месте сила притяжения ниже, чем на всей Земле в целом. Ученые объясняют это постепенным таянием ледников. Лед некогда сдвинул часть массы планеты. Сейчас же он активно тает. При этом планета не успевает восстановиться и перестроиться. Дополнительно уменьшению гравитации способствуют небольшая деформация коры в сочетании с перемещением магмы в мантии.
Аномальная гравитация на Луне
 Наглядный пример, как отличается земной шаг от шага на Луне. Credit: cooperandcary.com
Наглядный пример, как отличается земной шаг от шага на Луне. Credit: cooperandcary.com
Изучение гравитационного поля небесного тела проводилось посредством регистрации его влияния на орбиты искусственных спутников Луны. Данные, полученные космическими аппаратами «Луна-10» и «Лунар орбитер», не только помогли ответить на вопрос, есть ли гравитация на Луне, но и выявили ее особенности.
Исследования земного спутника показали, что гравитационное поле Луны неоднородно. Исследователи связывают эту особенность с концентрацией в толще лунных морей структур, имеющих высокую плотность. Ученые решили использовать для обозначения таких суперплотных фрагментов термин “масконы”. Высокая плотность этих геологических структур позволяет создавать выраженное возмущение в гравитационном поле земного спутника. Их действие на космические аппараты на лунной орбите способно влиять на курс космических объектов.
Механизм образования масконов научный мир связывает с накоплением и уплотнением материи космического объекта в той части кратера, которая погружена в мантию небесного тела. Сюда же, способствуя дальнейшему уплотнению, сползают и горные породы со склонов ударной воронки.
Другая теория образования лунных гравитационных аномалий указывает, что в области лунных морей образуется дополнительная сила притяжения. Это происходит в результате аккумулирования этими участками поверхности большего количества солнечный энергии. Ведь плоская, имеющая темный цвет поверхность быстрее и сильнее нагревается от солнечных лучей и гораздо медленнее остывает по сравнению с окружающим лунным грунтом.
Утверждается также, что некоторые из гравитационных аномалий связаны с упавшими и проникшими в лунную кору метеоритами, состоящими из вещества, имеющего высокую плотность.
Из истории гравитационной постоянной
Интересно, что в работах Ньютона нет такой величины. Она появилась в физике существенно позже. Если быть конкретнее, то только в начале девятнадцатого века. Но это не значит, что ее не было. Просто ученые ее не определили и не узнали ее точное значение. Кстати, о значении. Гравитационная постоянная постоянно уточняется, поскольку является десятичной дробью с большим количеством цифр после запятой, перед которой стоит ноль.
Именно тем, что эта величина принимает такое маленькое значение, объясняется то, что действие сил гравитации незаметно на небольших телах. Просто из-за этого множителя сила притяжения оказывается ничтожно маленькой.
Впервые опытным путем установил значение, которое принимает гравитационная постоянная, физик Г. Кавендиш. И случилось это в 1788 году.

В его опытах использовался тонкий стержень. Он был подвешен на тоненькой проволоке из меди и имел длину около 2 метров. К концам этого стержня были прикреплены два одинаковых свинцовых шара диаметром 5 см. Рядом с ними были установлены большие свинцовые шары. Их диаметр был уже 20 см.
При сближении больших и маленьких шаров наблюдался поворот стержня. Это говорило об их притяжении. По известным массам и расстоянию, а также измеренной силе закручивания удалось достаточно точно узнать, чему равно гравитационное постоянное.
Примечания[править | править код]
- В общей теории относительности обозначения, использующие букву G, применяются редко, поскольку там эта буква обычно используется для обозначения тензора Эйнштейна.
- По определению массы, входящие в это уравнение, — гравитационные массы, однако расхождения между величиной гравитационной и инертной массы какого-либо тела до сих пор не обнаружено экспериментально. Теоретически в рамках современных представлений они вряд ли отличаются. Это в целом было стандартным предположением и со времен Ньютона.
- (англ.). Дата обращения 7 марта 2020.
- Разные авторы указывают разный результат, от 6,754⋅10−11 м²/кг² до (6,60 ± 0,04)⋅10−11м³/(кг·с³) — см. .
- Ляховец В. Д. Проблемы метрологического обеспечения измерений гравитационной постоянной. // Проблемы теории гравитации и элементарных частиц. Выпуск 17. — М., Энергоатомиздат, 1986. — с. 122-125.
- Игорь Иванов. (13 сентября 2013). Дата обращения 14 сентября 2013.
- Brooks, Michael . NewScientist (21 сентября 2002).
- Результат: (dG/dt)/G = (−6,4 ± 2,2)×10−11 год−1
- Результат: |Ġ/G| ≤ 2,3 × 10−11 год−1
Эффект Пельтье, Томсон и температура
В 1856 году У. Томсон (лорд Кельвин) выдвинул гипотезу, что теплота, аналогичная теплоте эффекта Пельтье, должна выделяться (поглощаться) при прохождении тока по однородному проводнику, вдоль которого имеется градиент температуры . Эффект Пельтье, заключается в том, что при протекании электрического тока через разнородные спаи (соединения) двух металлов, в одном спае происходит выделение теплоты, а в другом — поглощение. Предсказанный Томсоном эффект в последствии был подтвержден экспериментально и получил название «явление Томсона», которое записывается следующим выражением:
Q – количество теплоты, выделяющееся в единицу времени в проводнике длиной dl.
I – сила тока, dΘ/dl – градиент температуры, τ – коэффициент, называемый коэффициентом Томсона.
Последуем за лордом Кельвином также, как он в свое время последовал за Пельтье, и используем вышеприведенную формулу для наших целей, но значение ее будет совершенно иным. Для чего заменим линейный размер тела на его объем.
k – коэффициент пропорциональности.
Сила тяготения dF, действующая в единицу времени в элементе вещества с объемом dV,пропорциональна интенсивности излучения I и градиенту температуры dΘ/dV.
Гравитация – это взаимообмен квантами энергии.
Примечания[править]
-
J. Dufour. “Very sizeable increase of gravity at pico-meter distance: a novel working hypothesis to explain anomalous heat effects and apparent transmutations in certain metal hydrogen systems”. J. of condensed matter nuclear science, Vol. 1, pp. 47-61 (2007).
- Strong Interactions, Gravitation and Cosmology. Abdus Salam Publ. in: NATO Advanced Study Institute, Erice, June16-July 6, 1972 ; in: High Energy Astrophysics and its Relation to Elementary Particle Physics, 441-452 MIT Press, Cambridge (1974).
- Sivaram, C. and Sinha, K.P. Strong gravity, black holes, and hadrons. Physical Review D, Vol. 16, Issue 6, pp. 1975-1978 (1977).
- Salam A. and Sivaram C. Strong Gravity Approach to QCD and Confinement. Mod. Phys. Lett., v. A8(4), pp. 321-326 (1993).
- Raut, Usha and Shina, KP (1983) Strong gravity and the fine structure constant. In: Proceedings of the Indian Academy of Sciences Part A: Physical Sciences, 49 (2). pp. 352-358.
- V. de Sabbata, C. Sivaram. Strong Spin-Torsion Interaction between Spinning Protons. Il Nuovo Cimento, Vol. 101A, N. 2, pp. 273-283 (1989).
- T. R. Mongan. Cold dark matter from «strong gravity». General Relativity & Quantum Cosmology, 20 Jun 2007; arXiv:0706.3050v2.
- Oldershaw R.L. Discrete Scale Relativity. Astrophysics and Space Science, Vol. 311, N. 4, pp. 431-433 (2007). DOI: 10.107/s10509-007-9557-x.
- Stone R.A. Quark Confinement and Force Unification. Progress in Physics, Vol. 2, pp. 19-20 (2010).
- K. Tennakone. Electron, muon, proton, and strong gravity. Phys. Rev. D, Volume 10, Issue 6, pp.1722-1725 (1974).
- Zane Andrea Quintili. Gravitational Field and Proton Radius. vixra.org. (2019).
- Recami, E.; Ammiraju, P.; Hernandez, H.E.; Kretly, L.C.; Rodrigues, W.A., Jr. Elementary particles as micro-universes: a geometric approach to «strong gravity». Apeiron, January 01, 1997.
- Recami E. and Tonin-Zanchin V. The strong coupling constant: its theoretical derivation from a geometric approach to hadron structure. Found. Phys. Lett., v, 7(1), pp. 85-92 (1994).
- Erasmo Recami, Tonin-Zanchin, Antonino Del Popolo, Mario Gambera. The strong coupling constant, Heavy Ion Physics, Vol. 10, pp. 345-349 (1999).
- Stanislav Fisenko & Igor Fisenko. The Conception of Thermonuclear Reactor on the Principle of Gravitational Confinement of Dense High-temperature Plasma. Applied Physics Research, Vol. 2, No. 2, pp. 71-79 (2010).
- S. I. Fisenko, M. M. Beilinson and B. G. Umanov. Some notes on the concept of “strong” gravitation and possibilities of its experimental investigation. Physics Letters A, Volume 148, Issues 8-9, pp. 405-407 (1990).
- U. V. S. Seshavatharam and S. Lakshminarayana. Strong nuclear gravitational constant and the origin of nuclear planck scale. Progress in Physics, vol. 3, pp. 31-38 (2010).
- Perng J. J. Strong gravitation and elementary particles. Nuovo Cimento, Lettere, Serie 2, vol. 23, N. 15, pp. 552-554 (1978).
- ↑ Федосин С. Г. Физика и философия подобия от преонов до метагалактик, Пермь: Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.
- Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
- Fedosin S.G. The radius of the proton in the self-consistent model. Hadronic Journal, Vol. 35, No. 4, pp. 349-363 (2012); статья на русском языке: Радиус протона в самосогласованной модели.
- Комментарии к книге: Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
- Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, Vol. 4, No. 1, pp. 1-24 (2009); статья на русском языке: Модель гравитационного взаимодействия в концепции гравитонов.
- Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, ISSN: 2348-0130, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197; статья на русском языке: Поле гравитонов как источник гравитационной силы и массы в модернизированной модели Лесажа.
- Fedosin S.G. The charged component of the vacuum field as the source of electric force in the modernized Le Sage’s model. Journal of Fundamental and Applied Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). http://dx.doi.org/10.4314/jfas.v8i3.18, https://dx.doi.org/10.5281/zenodo.845357; статья на русском языке: Заряженная компонента вакуумного поля как источник электрической силы в модернизированной модели Лесажа.
Притяжение Луны и Земли
Влияние земной гравитации на лунный ландшафт можно рассмотреть на примере лунных морей. На стороне спутника, обращенной к планете, их существенно больше — они составляют более 30% площади полушария. Для сравнения, на другом полушарии лунные моря занимают 2,5% площади поверхности.
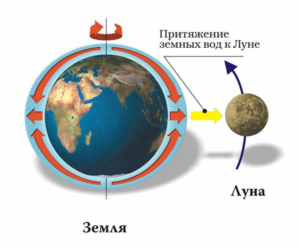 Схема притяжения земных вод к Луне. Credit: NASA
Схема притяжения земных вод к Луне. Credit: NASA
Лунные моря представляют собой относительно ровные участки поверхности небесного объекта, залитые застывшей лавой и покрытые пылью. Скопление их на обращенной к Земле стороне ученые объясняют действием силы земного притяжения. Если бы не приливные силы Земли, то лава распределилась бы по поверхности небесного тела равномерно.
Гравитационные силы Луны оказывают влияние на Землю. В первую очередь сила лунного тяготения сказывается на водных массах.
В науке популярно утверждение, что с этим влиянием связаны морские приливы и отливы:
- Прилив наблюдается на том полушарии, над которым находится в данный период спутник.
- Отлив является результатом того, что по мере движения небесных тел влияние гравитации Луны ослабевает.
Научный мир не смущают некоторые парадоксы. Например, влияние Солнца на земную поверхность во много раз больше по сравнению с влиянием спутника. Однако причиной подъема и спада уровня моря считают не его, а Луну.
Вывод гравитационной константы «Метод G-2001» и массы Солнца, Земли, Луны.
Текст от 1 апреля 2001 года: Подойдем к этой проблеме
гравитационной константы другой стороны. Может быть, G действительно испытывает
значительные вариации. Может быть, это связано с распространением гравитационных
волн длиной в несколько дней. А в этой работе, кстати, предсказан максимум
гравитационных колебаний длиной волны порядка 6 световых дней. Этот максимум
есть зеркальное отражение относительно граничной частоты между фотоном и
гравитоном. Этот максимум, по моему убеждению, ответственен за наличие циклонов
и антициклонов, за периодичность в изменении погоды. См.
Пространственно- временная симметрия. Тем не менее,
среднестатистическое значение гравитационной постоянной должно быть очень
точным.
В настоящей работе развиты Нормированные
Единицы, в которых граничная частота n,
граничная длина волны l, граничный
период колебаний t приняты равными единицам. Гравитационная
постоянная в нормированных единицах безразмерна, обозначена той же буквой
G, но со штрихом G’, и может быть получена по формулам:
или:
Последние результаты, полученные в январе феврале 2001 года,
показали, что второй вариант, где определяющей гравитирующей частицей является
атом водорода, оказывается предпочтительней. Поэтому, далее мы исследуем
именно второй вариант. Но что же прячется за буквой
s в последней формуле. В случае протона, как определяющей частицы,
мы вводили релятивистскую поправку в формулу G’ = 1/Exp(1/a).
В результате формула изуродовалась, а её хорошее приближение приобрело вид
G’ = 1/Exp(a+1/a).
В случае с водородом этого делать не хочется, и мы попробуем поискать, а
что же должно быть на месте s?
Разложим по полочкам приведенные выше формулы, содержащие
G’.
Формула 1: G’ = Gt2mH/l3
Формула 2 и 3: G’ = N(fgr/fel)H-el/(2p2)
= (a/e/G)1/2e/mel/2
Формула 4: 1/G’ = sExp(1/a)
Здесь мы попытаемся получить массы Земли, Луны, Солнца несколько
нетрадиционным способом. Прежде всего, укажем, что эти массы сильно отличаются
от справочника к справочнику. Поместим значения из разных справочников в
таблицу. В последнюю колонку, красным цветом я ввожу свои данные, которые
мы получим ниже, при условии нескольких «ЕСЛИ». То есть, результаты верны,
ЕСЛИ такие-то предположение верны… А сначала в таблице идут значения,
приведенные в современных справочных сайтах по состоянию на март 2001 года.
1. http://pdg.lbl.gov/
2. http://www.seds.org/nineplanets/nineplanets/earth.html
3.
http://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html
4. «устаревшие значения» из энциклопедического словаря по физике
за 1983 год, который переиздан в 1999 году.
5. Мои результаты (2001).
| . | 1 | 2 | 3 | 4 | 5 (если…!) |
| MEarth (*1024 кг) | 5.974(9) | 5.972 | 5.9736 | 5.976 | 5.973538542 |
| MMoon (*1022 кг) | — | 7.35 | 7.349 | 7.35 | 7.3463 |
| MSun (*1030 кг) | 1.9889(30) | 1.989 | 1.9891 | 1.989 | 1.988909058 |
| LSun (*1026 Вт) | 3.846(8) | 3.86 | 3.846 | 3.826 | 3.841740089 |
| GMSun (*1017 м3/с2) | — | — | 1.32712 | — | 1.327120783 |
| 2GMSun /c2 (км) | 2.95325008 | — | — | — | 2.953242026 |
| GMEarth (*1014 м3/с2) | — | — | 3.986 | — | 3.985907306 |
| 2GMEarth /c2 (мм) | 8.87005622 | — | — | — | 8.869839976 |
Давайте попытаемся постулировать следующие утверждения:
Имеем в виду, что полученные результаты верны, если работают
допущения «ЕСЛИ«.