Законы движения кеплера
Содержание:
- Математическое совпадение
- Соотношения между элементами эллипса
- Первый закон Кеплера (закон эллипсов)
- Исследования воздействия космоса на организм
- Полет по параболе
- Связанные определения
- Астрономия
- §7.1. Форма орбиты и скорость движения
- Определение
- Другие свойства
- Рудольфовы таблицы
- Современное состояние вопроса
Математическое совпадение
Возьмём треугольник Кеплера со сторонами a,aφ,aφ,{\displaystyle a,a{\sqrt {\varphi }},a\varphi ,} и рассмотрим:
- окружность, которая окружает его, и
- квадрат со стороной, равной средней по величине стороне треугольника.
Тогда периметр квадрата (4aφ{\displaystyle 4a{\sqrt {\varphi }}}) и длина окружности (aπφ{\displaystyle a\pi \varphi }) совпадают с точностью до 0,1 %.
Это математическое совпадение π≈4φ{\displaystyle \pi \approx 4/{\sqrt {\varphi }}}. Эти квадрат и окружность не могут иметь одинаковую длину периметра, поскольку в этом случае можно было бы решить классическую неразрешимую задачу о квадратуре круга. Другими словами, π≠4φ{\displaystyle \pi \neq 4/{\sqrt {\varphi }}} поскольку π{\displaystyle \pi } — трансцендентное число.
Соотношения между элементами эллипса
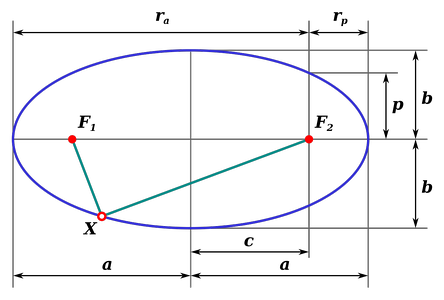 Части эллипса (описание см. в разделе «Связанные определения»)
Части эллипса (описание см. в разделе «Связанные определения»)
- a{\displaystyle {\boldsymbol {a}}} — большая полуось;
- b{\displaystyle {\boldsymbol {b}}} — малая полуось;
- c{\displaystyle {\boldsymbol {c}}} — фокальное расстояние (полурасстояние между фокусами);
- p{\displaystyle {\boldsymbol {p}}} — фокальный параметр;
- rp{\displaystyle {\boldsymbol {r}}_{p}} — перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
- ra{\displaystyle {\boldsymbol {r}}_{a}} — апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);
a2=b2+c2{\displaystyle a^{2}=b^{2}+c^{2}};
e=ca=1−b2a2(⩽e<1){\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}\;\;\;(0\leqslant e<1)};
p=b2a{\displaystyle p={\frac {b^{2}}{a}}}.
| a{\displaystyle {\boldsymbol {a}}} | b{\displaystyle {\boldsymbol {b}}} | c{\displaystyle {\boldsymbol {c}}} | p{\displaystyle {\boldsymbol {p}}} | rp{\displaystyle {\boldsymbol {r_{p}}}} | ra{\displaystyle {\boldsymbol {r_{a}}}} | |
|---|---|---|---|---|---|---|
| a{\displaystyle {\boldsymbol {a}}} — большая полуось | a{\displaystyle {\boldsymbol {a}}} | a=b1−e2{\displaystyle a={\frac {b}{\sqrt {1-e^{2}}}}} | a=ce{\displaystyle a={\frac {c}{e}}} | a=p1−e2{\displaystyle a={\frac {p}{1-e^{2}}}} | a=rp1−e{\displaystyle a={\frac {r_{p}}{1-e}}} | a=ra1+e{\displaystyle a={\frac {r_{a}}{1+e}}} |
| b{\displaystyle {\boldsymbol {b}}} — малая полуось | b=a1−e2{\displaystyle b=a{\sqrt {1-e^{2}}}} | b{\displaystyle {\boldsymbol {b}}} | b=c 1−e2e{\displaystyle b={\frac {c~{\sqrt {1-e^{2}}}}{e}}} | b=p1−e2{\displaystyle b={\frac {p}{\sqrt {1-e^{2}}}}} | b=rp1+e1−e{\displaystyle b=r_{p}{\sqrt {\frac {1+e}{1-e}}}} | b=ra1−e1+e{\displaystyle b=r_{a}{\sqrt {\frac {1-e}{1+e}}}} |
| c{\displaystyle {\boldsymbol {c}}} — фокальное расстояние | c=ae{\displaystyle c=ae} | c=be1−e2{\displaystyle c={\frac {be}{\sqrt {1-e^{2}}}}} | c{\displaystyle {\boldsymbol {c}}} | c=pe1−e2{\displaystyle c={\frac {pe}{1-e^{2}}}} | c=rpe1−e{\displaystyle c={\frac {r_{p}e}{1-e}}} | c=rae1+e{\displaystyle c={\frac {r_{a}e}{1+e}}} |
| p{\displaystyle {\boldsymbol {p}}} — фокальный параметр | p=a(1−e2){\displaystyle p=a(1-e^{2})} | p=b 1−e2{\displaystyle p=b~{\sqrt {1-e^{2}}}} | p=c 1−e2e{\displaystyle p=c~{\frac {1-e^{2}}{e}}} | p{\displaystyle {\boldsymbol {p}}} | p=rp(1+e){\displaystyle p=r_{p}(1+e)} | p=ra(1−e){\displaystyle p=r_{a}(1-e)} |
| rp{\displaystyle {\boldsymbol {r}}_{p}} — перифокусное расстояние | rp=a(1−e){\displaystyle r_{p}=a(1-e)} | rp=b 1−e1+e{\displaystyle r_{p}=b~{\sqrt {\frac {1-e}{1+e}}}} | rp=c 1−ee{\displaystyle r_{p}=c~{\frac {1-e}{e}}} | rp=p1+e{\displaystyle r_{p}={\frac {p}{1+e}}} | rp{\displaystyle {\boldsymbol {r}}_{p}} | rp=ra1−e1+e{\displaystyle r_{p}=r_{a}{\frac {1-e}{1+e}}} |
| ra{\displaystyle {\boldsymbol {r}}_{a}} — апофокусное расстояние | ra=a(1+e){\displaystyle r_{a}=a(1+e)} | ra=b 1+e1−e{\displaystyle r_{a}=b~{\sqrt {\frac {1+e}{1-e}}}} | ra=c 1+ee{\displaystyle r_{a}=c~{\frac {1+e}{e}}} | ra=p1−e{\displaystyle r_{a}={\frac {p}{1-e}}} | ra=rp 1+e1−e{\displaystyle r_{a}=r_{p}~{\frac {1+e}{1-e}}} | ra{\displaystyle {\boldsymbol {r}}_{a}} |
Первый закон Кеплера (закон эллипсов)
Первый закон Кеплера.
Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.
Форма эллипса и степень его сходства с окружностью характеризуется отношением e=ca{\displaystyle e={\frac {c}{a}}}, где c{\displaystyle c} — расстояние от центра эллипса до его фокуса (фокальное расстояние), a{\displaystyle {a}} — большая полуось. Величина e{\displaystyle e} называется эксцентриситетом эллипса. При c={\displaystyle c=0}, и, следовательно, e={\displaystyle e=0} эллипс превращается в окружность.
Доказательство первого закона Кеплера
Закон всемирного тяготения Ньютона гласит, что «каждый объект во Вселенной притягивает каждый другой объект по линии, соединяющей центры масс объектов, пропорционально массе каждого объекта, и обратно пропорционально квадрату расстояния между объектами». Это предполагает, что ускорение a{\displaystyle a} имеет форму
- a=d2rdt2=f(r)r^.{\displaystyle \mathbf {a} ={\frac {d^{2}\mathbf {r} }{dt^{2}}}=f(r){\hat {\mathbf {r} }}.}
Вспомним, что в полярных координатах
- drdt=r˙r^+rθ˙θ^,{\displaystyle {\frac {d\mathbf {r} }{dt}}={\dot {r}}{\hat {\mathbf {r} }}+r{\dot {\theta }}{\hat {\boldsymbol {\theta }}},}
- d2rdt2=(r¨−rθ˙2)r^+(rθ¨+2r˙θ˙)θ^.{\displaystyle {\frac {d^{2}\mathbf {r} }{dt^{2}}}=({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {\mathbf {r} }}+(r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}){\hat {\boldsymbol {\theta }}}.}
В координатной форме запишем
- r¨−rθ˙2=f(r),{\displaystyle {\ddot {r}}-r{\dot {\theta }}^{2}=f(r),}
- rθ¨+2r˙θ˙={\displaystyle r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}=0.}
Подставляя θ¨{\displaystyle {\ddot {\theta }}} и r˙{\displaystyle {\dot {r}}} во второе уравнение, получим
- rdθ˙dt+2drdtθ˙=,{\displaystyle r{d{\dot {\theta }} \over dt}+2{dr \over dt}{\dot {\theta }}=0,}
которое упрощается
- dθ˙θ˙=−2drr.{\displaystyle {\frac {d{\dot {\theta }}}{\dot {\theta }}}=-2{\frac {dr}{r}}.}
После интегрирования запишем выражение
- lnθ˙=−2lnr+lnℓ,{\displaystyle \ln {\dot {\theta }}=-2\ln r+\ln \ell ,}
- lnℓ=lnr2+lnθ˙,{\displaystyle \ln \ell =\ln r^{2}+\ln {\dot {\theta }},}
- ℓ=r2θ˙,{\displaystyle \ell =r^{2}{\dot {\theta }},}
для некоторой константы ℓ{\displaystyle \ell }, которая является удельным угловым моментом (ℓ=r×v{\displaystyle \ell =\mathbf {r} \times \mathbf {v} }).
Пусть
- r=1u,{\displaystyle r={\frac {1}{u}},}
- r˙=−1u2u˙=−1u2dθdtdudθ=−ℓdudθ,{\displaystyle {\dot {r}}=-{\frac {1}{u^{2}}}{\dot {u}}=-{\frac {1}{u^{2}}}{\frac {d\theta }{dt}}{\frac {du}{d\theta }}=-\ell {\frac {du}{d\theta }},}
- r¨=−ℓddtdudθ=−ℓθ˙d2udθ2=−ℓ2u2d2udθ2.{\displaystyle {\ddot {r}}=-\ell {\frac {d}{dt}}{\frac {du}{d\theta }}=-\ell {\dot {\theta }}{\frac {d^{2}u}{d\theta ^{2}}}=-\ell ^{2}u^{2}{\frac {d^{2}u}{d\theta ^{2}}}.}
Уравнение движения в направлении r^{\displaystyle {\hat {\mathbf {r} }}} становится равным
- d2udθ2+u=−1ℓ2u2f(1u).{\displaystyle {\frac {d^{2}u}{d\theta ^{2}}}+u=-{\frac {1}{\ell ^{2}u^{2}}}f\left({\frac {1}{u}}\right).}
Закон всемирного тяготения Ньютона связывает силу на единицу массы с расстоянием как
- f(1u)=f(r)=−GMr2=−GMu2{\displaystyle f\left({1 \over u}\right)=f(r)=-\,{GM \over r^{2}}=-GMu^{2}}
где G{\displaystyle G} — универсальная гравитационная константа и M{\displaystyle M} — масса звезды.
В результате
- d2udθ2+u=GMℓ2.{\displaystyle {\frac {d^{2}u}{d\theta ^{2}}}+u={\frac {GM}{\ell ^{2}}}.}
Это дифференциальное уравнение имеет общее решение:
- u=GMℓ21+ecos(θ−θ).{\displaystyle u={\frac {GM}{\ell ^{2}}}\left.}
для произвольных констант интегрирования e{\displaystyle e} и θ{\displaystyle \theta _{0}}.
Заменяя u{\displaystyle u} на 1/r{\displaystyle r} и полагая θ={\displaystyle \theta _{0}=0}, получим:
- r=1u=ℓ2GM1+ecosθ.{\displaystyle r={1 \over u}={\frac {\ell ^{2}/GM}{1+e\cos \theta }}.}
Мы получили уравнение конического сечения с эксцентриситетом e{\displaystyle e} и началом системы координат в одном из фокусов. Таким образом, первый закон Кеплера прямо следует из закона всемирного тяготения Ньютона и второго закона Ньютона.
Исследования воздействия космоса на организм
Также ученые путем экспериментов и исследований выяснили, что пребывание в невесомости сказывается на иммунной системе организма. Другими словами, человек сильнее подвержен различным заболеваниям, поскольку ухудшается его иммунитет. Если говорить простым языком, то суть работы иммунной системы – отыскать в организме чужеродный микроорганизм и атаковать его.
Исследования проводила группа ученых NASA с привлечением 23 космонавтов (мужчин и женщин) в возрасте около 53 лет. Космонавты находились в условиях невесомости разное количество времени. Необходимые анализы им сделали до вылета, некоторые участники эксперимента брали у себя кровь, находясь на станции. Затем обследования проводились по прибытию космонавтов на Землю сразу и спустя определенные промежутки времени.
Таким образом, удалось сравнить результаты и выяснить, что иммунитет космонавтов, которые работали на МКС полгода, значительно ухудшился по сравнению с остальными участниками исследований. В частности, существенно снизилась способность иммунной системы распознавать угрозу и устранять ее. По возвращению космонавтов на Землю работа иммунитета начала медленно восстанавливаться. Точная причина таких изменений не установлена, поскольку это может быть стресс, нарушение работы биологических часов, нахождение в невесомости.
Еще одно исследование проводилось по влиянию невесомости на кожу организма. Космонавты часто жаловались на возникновение зуда кожи и сухости. Для эксперимента на орбиту отправили мышей сроком на три месяца. Обследование вернувшихся из космоса грызунов показали, что кожный покров истончился на 15%, а также изменился рост шерсти. Причем изменения происходили на уровне генов.
Интересный факт: при помощи мышей установлено и влияние невесомости на зрение. Их отправляли в космическое пространство на месяц, после чего проанализировали состояние глаз. Ученые выяснили, что зрение ухудшается из-за нарушенной деятельности кровеносных сосудов. Для организма всех живых существ естественно то, что кровь под действие гравитации устремляется к ногам. В невесомости она оказывает давление на мозг, что и наносит вред работе сосудов.
В невесомости кровь оказывает давление на мозг
Космонавты, работающие на МКС, часто жалуются на ухудшение зрения. По прибытию их на Землю зрение тоже постепенно возвращается к прежнему состоянию, но, как и в случае с другими органами и системами, все зависит от длительности нахождения в космосе. Ученые активно занимаются поиском решений, которые помогут снизить влияние невесомости на человеческий организм.
Невесомость несвойственна для человеческого организма. Многие его системы зависимы от силы притяжения, поэтому отсутствие гравитации негативно сказывается на здоровье космонавтов. Ухудшается работа опорно-двигательного аппарата, сердечнососудистой системы, ослабевают мышцы, зрение, иммунитет, состояние кожи. Пагубный эффект невесомости зависит от того, насколько долго космонавт пребывает в космосе. Для профилактики различных заболеваний и проблем используется специальное снаряжение, а космонавты тщательно готовятся к отправке в космос.
Полет по параболе
«Сказочники! — улыбается один из летчиков, заместитель командира полка Игорь Клименко. — для таких полетов выделяется специальная зона и высоты от шести до десяти тысяч метров при условии отсутствия облачности, и никаких коммерческих рейсов там не может быть в принципе. Обычно мы летаем в районе Плещеева озера, по нему удобно визуально ориентироваться». Полет выполняется по так называемой параболе Кеплера и начинается с горизонтального разгона на высоте примерно 6500 м. Затем самолет делает «горку» — на восходящей части происходит ввод в режим невесомости, при этом перегрузка достигает двух единиц. «Управление осуществляется вручную, — объясняет Игорь, — при этом нагрузка на штурвале составляет примерно 70 кгс. Представьте себе штангу такой массы, только поднимать ее нужно не рывком, а плавно и с ювелирной точностью. Причем необходимо очень тщательно следить за креном и боковым смещением — они должны быть нулевые, иначе тех, кто в салоне, ‘размажет’ по стенам». Из-за больших физических нагрузок командир и второй пилот, как правило, выполняют режимы невесомости по очереди.
При достижении угла кабрирования примерно в 50 градусов летчик «отдает» штурвал от себя, вводит самолет в 25−30-секундный режим невесомости и осуществляет контроль по индикатору перегрузки и по упомянутому выше «стаканчику». С высоты примерно 9500 м самолет пикирует и переходит (опять-таки с перегрузкой до двух единиц) в горизонтальный полет. Несколько минут такого полета требуется для того, чтобы выполнить разворот, а также зарядить топливные и масляные аккумуляторы. «Формально разрешается выполнять три режима без ‘перезарядки’, а технически ‘запас прочности’ еще в три раза выше, — говорит Игорь Клименко. — но зачем лишний раз рисковать, если в этом нет никакой необходимости? Безопасность для нас всегда приоритетна». Затем все повторяется — за один полет Ил-76МДК выполняет в среднем десять режимов невесомости.
Boeing 727−200 G-Force One (Zero-G)
Связанные определения
- Проходящий через фокусы эллипса отрезок AB, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
- Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
- Точка пересечения большой и малой осей эллипса называется его центром.
- Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
- Расстояния r1{\displaystyle r_{1}} и r2{\displaystyle r_{2}} от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
- Расстояние c=|F1F2|2{\displaystyle c={\frac {|F_{1}F_{2}|}{2}}} называется фокальным расстоянием.
- Величина e=ca=1−b2a2{\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}} называется эксцентриситетом.
- Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
- Радиус эллипса в данной точке это отрезок, соединяющий центр эллипса с точкой, а также его длина, которая вычисляется по формуле r=abb2cos2φ+a2sin2φ=b1−e2cos2φ{\displaystyle r={\frac {ab}{\sqrt {b^{2}\cos ^{2}\varphi +a^{2}\sin ^{2}\varphi }}}={\frac {b}{\sqrt {1-e^{2}\cos ^{2}\varphi }}}}, где φ{\displaystyle \varphi } — угол между радиусом и большой полуосью.
- Фокальным параметром p=b2a{\displaystyle p={\frac {b^{2}}{a}}} называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса.
- Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью: k=ba{\displaystyle k={\frac {b}{a}}}. Величина, равная (1−k)=a−ba,{\displaystyle (1-k)={\frac {a-b}{a}},} называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент сжатия и эксцентриситет эллипса связаны соотношением k2=1−e2.{\displaystyle k^{2}=1-e^{2}.}
- Для каждого из фокусов существует прямая, называемая директрисой, такая, что отношение расстояния от произвольной точки эллипса до его фокуса к расстоянию от этой точки до данной прямой равно эксцентриситету эллипса. Весь эллипс лежит по ту же сторону от такой прямой, что и фокус. Уравнения директрис эллипса в каноническом виде записываются как x=±pe(1−e2){\displaystyle x=\pm {\frac {p}{e\left(1-e^{2}\right)}}} для фокусов (±pe1−e2,){\displaystyle \left(\pm {\frac {pe}{1-e^{2}}},\,0\right)} соответственно. Расстояние между фокусом и директрисой равно pe{\displaystyle {\frac {p}{e}}}.
Астрономия
Учебник для 10 класса
Законы движения планет и искусственных небесных тел
§7.1. Форма орбиты и скорость движения
Чем ближе планета к Солнцу, тем, больше ее линейная и угловая скорости и короче период обращения вокруг Солнца. Мы наблюдаем планеты с Земли, которая сама обращается вокруг Солнца. Это движение Земли необходимо учитывать, чтобы узнать периоды обращения планет в невращающей-ся инерциальной системе отсчета, или, как часто говорят, по отношению к звездам.
Период обращения планет вокруг Солнца по отношению к звездам называется звездным или сидерическим периодом. Наименьший звездный период обращения у планеты Меркурий — 88 сут. У Марса он составляет почти 2 года, а у Юпитера — 12 лет и, все возрастая с удалением от Солнца, у Плутона доходит почти до 250 лет. Заслуга открытия законов движения планет принадлежит выдающемуся немецкому ученому Иоганну Кеплеру. В начале XVII в. Кеплер установил три закона движения планет. Они названы законами Кеплера.
Первый закон Кеплера: каждая планета обращается по эллипсу, в одном из фокусов которого находится Солнце (рис. 24).
Рис. 24. Закон площадей (второй закон Кеплера).
Эллипсом (рис. 24) называется плоская замкнутая кривая, имеющая такое свойство, что сумма расстояний каждой ее точки от двух точек, называемых фокусами, остается постоянной. Эта сумма расстояний равна длине большой оси DA эллипса (рис. 24). Точка О — центр эллипса, К и S — фокусы. Солнце находится в данном случае в фокусе S. DO = О А = а — большая полуось эллипса. Большая полуось а является средним расстоянием планеты от Солнца:
Ближайшая к Солнцу точка 0рбиты а называется перигеем, а самая далекая от него точка называется афели м.
Рис. Иоганн Кеплер (1571-1630). Выдающийся немецкий астроном и математик, открывший законы движения планет вокруг Солнца. Кеплер был активным сторонником учения Коперника и своими работами способствовал его утверждению и развитию.
Степень вытянутости эллипса характеризуется его эксцентриситетом е. Эксцентриситет равен отношению расстояния фокуса от центра (ОК = OS) к длине большой полуоси а, т. е.
При совпадении фокусов с центром (е = 0) эллипс превращается в окружность.
Орбиты планет — эллипсы, мало отличающиеся от окружностей, их эксцентриситеты малы. Например, эксцентриситет орбиты Земли е = 0,017.
Эксцентриситеты орбит у большинства комет близки к единице. При е = 1 второй фокус эллипса удаляется в бесконечность, так что орбита становится разомкнутой кривой (рис. 25), называемой параболой. При е > 1 орбита является гиперболой (рис. 25). Двигаясь по параболе или гиперболе, тело только однажды огибает Солнце и навсегда удаляется от него.
Рис. 25. Формы орбит космических ракет(посланные по стрелке, они не вернутся, если пойдут по параболе или гиперболе, и по прерывистым частям кривых движения не будет).
Кеплер открыл свои законы, изучая периодическое обращение Марса вокруг Солнца. Ньютон, исходя из наблюдений движения Луны и законов Кеплера, открыл закон всемирного тяготения. При этом он доказал, что под действием взаимного тяготения тела могут двигаться друг относительно друга по эллипсу (в частности, по кругу), по параболе и по гиперболе. Ньютон установил, что вид орбиты, которую описывает тело, зависит от его скорости в данном месте орбиты.
При некоторой скорости тело описывает окружность около притягивающего центра. Такую скорость называют первой космической или круговой скоростью, ее сообщают телам, запускаемым в качестве искусственных спутников Земли по круговым орбитам. Вывод формулы для вычисления первой космической скорости известен из курса физики. Первая космическая скорость вблизи поверхности Земли составляет около 8 км/с (7,9 км/с).
Если телу сообщить скорость, в раза большую круговой (11,2 км/с), называемую второй космической или параболической скоростью, то тело навсегда удалится от Земли и может стать спутником Солнца. В этом случае движение тела будет происходить по параболе относительно Земли. При еще большей скорости относительно Земли тело полетит по гиперболе.
Средняя скорость движения Земли по орбите 30 км/с. Орбита Земли близка к окружности, а скорость движения Земли по орбите близка к круговой на расстоянии Земли от Солнца. Параболическая скорость на расстоянии Земли от Солнца равна 30км/с = 42 км/с. При такой скорости относительно Солнца тело с орбиты Земли покинет Солнечную систему.
Определение
Эллипс — геометрическое место точек M евклидовой плоскости, для которых сумма расстояний до двух данных точек F1{\displaystyle F_{1}} и F2{\displaystyle F_{2}} (называемых фокусами) постоянна и больше расстояния между фокусами, то есть
- |F1M|+|F2M|=2⋅a{\displaystyle |F_{1}M|+|F_{2}M|=2\cdot a}, причём |F1F2|<2⋅a{\displaystyle |F_{1}F_{2}|<2\cdot a}.
Другие определения
Эллипс также можно определить как:
- фигуру, которую можно получить из окружности, применяя аффинное преобразование
- ортогональную проекцию окружности на плоскость
- пересечение плоскости и кругового цилиндра.
Другие свойства
- Оптические
- Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
- Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
- Если F1{\displaystyle F_{1}} и F2{\displaystyle F_{2}} — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой (F1X){\displaystyle (F_{1}X)} равен углу между этой касательной и прямой (F2X){\displaystyle (F_{2}X)}.
- Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки
Эквивалентная формулировка: через середины двух любых параллельных хорд эллипса проходит какой-либо диаметр эллипса. В свою очередь, любой диаметр эллипса всегда проходит через центр эллипса.
легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
- Эволютой эллипса является астроида, вытянутая вдоль вертикальной оси.
- Точки пересечения эллипса с осями являются его вершинами.
-
Эксцентриситет эллипса, то есть отношение e=ca=1−b2a2(⩽e<1),{\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}\;\;\;(0\leqslant e<1),}
Если эксцентриситет эллипса равен нулю (что то же самое, что фокальное расстояние равно нулю: F1F2=0{\displaystyle F_{1}F_{2}=0}), то эллипс вырождается в окружность.
характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
- Экстремальные свойства
Если F{\displaystyle F} — выпуклая фигура и Tn{\displaystyle T_{n}} — вписанный в F{\displaystyle F} n{\displaystyle n}-угольник максимальной площади, то
S(Tn)≥S(F)⋅nsin(2⋅π/n)2⋅π,{\displaystyle S(T_{n})\geq S(F)\cdot {\frac {n}{\sin(2\cdot \pi /n)}}{2\cdot \pi },}
-
- где S(F){\displaystyle S(F)} обозначает площадь фигуры F{\displaystyle F}
Более того: равенство достигается в том и только в том случае, если F{\displaystyle F} ограничено эллипсом.
.
Среди всех выпуклых замкнутых кривых, ограничивающих данную площадь, эллипсы и только они имеет максимальную аффинную длину.
- где S(F){\displaystyle S(F)} обозначает площадь фигуры F{\displaystyle F}
Если произвольный эллипс вписан в треугольник ABC и имеет фокусы P и Q, тогда для него справедливо соотношение
-
- PA¯⋅QA¯CA¯⋅AB¯+PB¯⋅QB¯AB¯⋅BC¯+PC¯⋅QC¯BC¯⋅CA¯=1.{\displaystyle {\frac {{\overline {PA}}\cdot {\overline {QA}}}{{\overline {CA}}\cdot {\overline {AB}}}}+{\frac {{\overline {PB}}\cdot {\overline {QB}}}{{\overline {AB}}\cdot {\overline {BC}}}}+{\frac {{\overline {PC}}\cdot {\overline {QC}}}{{\overline {BC}}\cdot {\overline {CA}}}}=1.}
Если лестницу (бесконечно тонкий отрезок прямой) прислонить к вертикальной стенке с горизонтальным полом, и один конец лестницы будет скользить по стенке (всё время касаясь её) а второй конец лестницы будет скользить по полу (всё время касаясь его), тогда любая фиксированная точка лестницы (не на её концах), будет двигаться по дуге некоторого эллипса. Это свойство остаётся верным, если мы возьмём точку не внутри лестницы-отрезка, а на её мыслимом продолжении. Последнее свойство используется в описанном выше.mw-parser-output .ts-Переход img{margin-left:.285714em} эллипсографе.
Касательная, проходящая через точку (x0,y0){\displaystyle (x_{0},y_{0})}, принадлежащую эллипсу, имеет следующее уравнение:
- xxa2+yyb2=1.{\displaystyle {\frac {xx_{0}}{a^{2}}}+{\frac {yy_{0}}{b^{2}}}=1.}
Рудольфовы таблицы
Осенью 1598 года в Штирии начались гонения на протестантов. Кеплеру вместе с многими единоверцами пришлось покинуть Грац, но через месяц ему в виде исключения позволили вернуться и продолжить работу в качестве окружного математика. Тем не менее из-за изгнания ректора и почти всех учителей занятия в школе прекратились. Кеплеру стало ясно, что будущего в Граце у него нет. Он предпринимал лихорадочные попытки найти место за пределами Австрии, но безуспешно.
И тут помог Тихо Браге, который к этому времени стал придворным математиком императора Священной Римской империи и короля Богемии Рудольфа II. В декабре 1599 года Браге вторично пригласил Кеплера в целях совместной работы. Еще до получения этого письма Кеплер отправился в имперскую столицу Прагу в надежде стать ассистентом Браге. 4 февраля ученые встретились, и после этого свидания их жизненные линии уже не расплетались, хотя личные отношения оказались очень непростыми. Браге попросил императора взять Кеплера на службу, дабы тот смог обработать его архивы и составить на их основе самые совершенные таблицы планетных движений. Эти таблицы Браге предложил назвать в честь императора — Рудольфовыми. План монарху понравился, и он дал согласие.
Первоначально предполагалась, что для Кеплера создадут специальную должность. Однако вскоре Тихо Браге скоропостижно скончался (среди причин смерти назывались и детективные версии). Через два дня после похорон Браге Кеплера назначили придворным математиком с годовым окладом 500 флоринов. Правда, императорская казна перманентно пустовала и Кеплеру хронически не доплачивали. Однако он получил часть архива Браге — ту, которая относилась к движениям Марса. Эти материалы и легли в основу кеплеровской теории планетных движений, обессмертившей имя своего создателя.
Современное состояние вопроса
Макет космического аппарата Gaia на салоне Ле Бурже, 2013
В настоящее время наземные оптические измерения позволяют в некоторых случаях снизить ошибку в измерении параллакса до 0,005″, что соответствует предельному расстоянию в 200 пк. Дальнейшее повышение точности измерений стало возможным благодаря использованию космических телескопов. Специально для астрометрических целей Европейским космическим агентством (ЕКА) в 1989 году был запущен космический телескоп Hipparcos, позволивший измерить параллаксы более 100 тысяч звёзд с точностью до 0,001″. В 2013 году ЕКА запустило новый космический телескоп — Gaia. Планируемая точность измерения параллакса ярких звёзд (до 15 m) будет выше 25 миллионных долей секунды, для слабых звёзд (около 20 m) — до 300 миллионных долей секунды. Измерение годичных параллаксов позволяет производить также один из инструментов Космического телескопа им. Хаббла — Широкоугольная камера 3. Точность измерения параллаксов составляет от 20 до 40 миллионных долей секунды, что позволяет измерять расстояния до 5 килопарсек. В частности, был измерен параллакс переменной звезды SU Возничего.
Значительным достижением конца XX века явилось использование для параллактических измерений метода сверхдальной радиоинтерферометрии. Погрешность при этом может составлять до 10 миллионных долей угловой секунды. Этот метод применяется для измерения расстояния до компактных радиоисточников — космических мазеров, радиопульсаров и др. Так, с помощью этого метода удалось измерить расстояние до объекта Стрелец B2 — газопылевого облака с бурным звездообразованием, находящимся в 100-120 парсеках от центра нашей Галактики. Результаты измерений показали, что Стрелец B2 расположен на расстоянии 7,8±0,8 кпк, что даёт расстояние до центра Галактики 7,9±0,8 кпк. Измерение параллаксов ультракомпактных внегалактических радиоисточников является одной из целей планируемого российского космического эксперимента Миллиметрон — космической обсерватории миллиметрового, субмиллиметрового и инфракрасного диапазонов.