Объясняем законы ньютона для чайников

Первый закон Ньютона[править]

Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы или векторная сумма всех действующих сил (то есть равнодействующая) равна нулю. Чтобы изменить скорость движения, на тело необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.

Современная формулировкаправить

В современной физике первый закон Ньютона принято формулировать в следующем виде

Под свободной материальной точкой в данной формулировке понимается материальная точка, на которую не оказывается никакого внешнего воздействия, однако закон верен также для случая взаимно скомпенсированных внешних сил (это следует из 2-го закона Ньютона, так как скомпенсированные силы сообщают телу нулевое суммарное ускорение).

Историческая формулировкаправить

Ньютон в своей книге «Математические начала натуральной философии» сформулировал первый закон механики в следующем виде:

С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» надо заменить на «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает. С другой стороны, в произвольной (скажем, вращающейся) системе отсчёта закон инерции неверен. Поэтому ньютоновская формулировка нуждается в уточнениях.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Утверждение, что материальная точка покоится или движется равномерно прямолинейно, если на неё не действуют другие тела или действие на неё других тел взаимно уравновешено,

1) неверно ни для каких систем отсчёта 2) верно для инерциальных систем отсчёта 3) верно для неинерциальных систем отсчёта 4) верно при любых условиях

2. Система отсчёта, связанная с Землёй, может считаться инерциальной. Система отсчёта, связанная с автобусом, тоже будет инерциальной, если он

1) движется равномерно по извилистой дороге 2) тормозит у остановки 3) отъезжает от светофора 4) движется равномерно по прямолинейному участку пути

3. В каком из приведённых примеров тело движется по инерции:

1) равномерно движущийся по горизонтальной дороге автомобиль 2) автомобиль, движущийся по горизонтальной дороге с выключенным двигателем 3) автомобиль, поворачивающий направо 4) автомобиль, выезжающий со стоянки

4. Яблоко, лежащее неподвижно на столе вагона движущегося поезда покатился вправо, если смотреть по ходу поезда. Как изменилось движение поезда?

1) скорость поезда увеличилась 2) скорость поезда уменьшилась 3) поезд повернул влево 4) поезд повернул вправо

5. Можно ли считать инерциальной системой отсчёта движущийся автомобиль?

1) можно всегда 2) можно, только если он движется равномерно и прямолинейно 3) можно только во время разгона и торможения 4) нельзя ни при каких условиях

6. Массивный груз подвешен на тонкой нити 1. К грузу прикреплена такая же нить 2. Если медленно тянуть за нить 2, то оборвётся

1) только нить 1 2) только нить 2 3) нить 1 и нить 2 одновременно 4) либо нить 1, либо нить 2, в зависимости от массы груза

7. Нить, привязанная одним концом к вбитому в стену гвоздю, разорвётся, если другой её конец тянуть с силой не менее 50 Н. Чему равно наименьшее значение сил, с которыми растягивают эту же нить за оба конца, при котором она рвётся?

1) 25 Н 2) 50 Н 3) 75 Н 4) 100 Н

8. Два ученика тянут динамометр в противоположные стороны с силой 60 Н каждый. Каково показание динамометра?

1) 0 Н 2) 30 Н 3) 60 Н 4) 120 Н

9. Земля притягивает яблоко с силой ​\( \vec{F}_1 \)​. Яблоко притягивает Землю с силой \( \vec{F}_2 \). При этом

1) ​\( F_2 = 0 \)​ 2) ​\( F_1=F_2 \)​ 3) \( F_1>F_2 \) 4) \( F_1<F_2 \)

10. Чему равна масса автомобиля, трогающегося с места с ускорением 0,6 м/с2, если развиваемая им сила тяги равна 15 000 Н? Сила сопротивления, действующая на автомобиль, равна 6000 Н.

1) 1,5 т 2) 7,5 т 3) 15 т 4) 75 т

11. Из приведенных утверждений выберите два правильных и запишите их номера в таблицу.

1) законы Ньютона справедливы во всех системах отсчета 2) первый закон Ньютона утверждает существование инерциальных систем отсчета 3) равнодействующая сил действия и противодействия равна нулю 4) силы действия и противодействия имеют одинаковую природу 5) второй закон Ньютона говорит о том, что масса тела прямо пропорциональна действующей на тело силе

12. Два тела движутся по оси ​\( Ox \)​. На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.

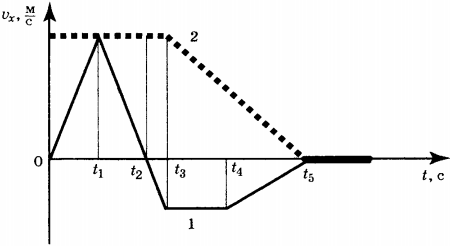
Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) В промежутке времени ​\( t_3-t_5 \)​ на тело 2 действует постоянная сила. 2) В промежутке времени ​\( 0-t_3 \)​ сила сообщает телу 1 положительное ускорение 3) В промежутке времени ​\( t_4-t_5 \)​ на тело 1 сила не действует 4) Модуль силы, действующей на тело 1 в промежутки времени ​\( 0-t_1 \)​, ​\( t_1-t_2 \)​ различен. 5) В промежутке времени ​\( t_1-t_2 \)​ сила сообщает телу 1 отрицательное ускорение

Часть 2

13. Тело массой 7 кг с помощью каната начинают равноускоренно поднимать вертикально вверх. Чему равна сила, действующая на тело со стороны каната, если известно, что за 4 с груз был поднят на высоту 16 м?

Второй закон

Данное научное обоснование касается не просто движения предметов в пространстве, а взаимодействия их с другими объектами и результатов этого процесса.

Закон гласит: увеличение скорости объекта с некоторой постоянной массой в инерциальной системе отсчета прямо пропорционально силе воздействия и обратно пропорционально постоянной массе движущегося предмета.

Проще говоря, если существует некое движущиеся тело, масса которого не изменяется, и на него вдруг начнет воздействовать посторонняя сила, то оно начнет ускоряться. А вот скорость ускорения будет прямо зависеть от воздействия и обратно пропорционально зависеть от массы движущегося предмета.

Для примера можно рассмотреть снеговой шар, который катиться с горы. Если шар толкать по ходу движения, то ускорения шара будет зависеть от мощности воздействия: чем она больше, тем больше ускорение. Но, чем больше масса данного шара, тем меньше будет ускорение. Данное явление описывается формулой, в которой учитывается ускорение, или «a», равнодействующая масса всех воздействующих сил, или «F», а также масса самого предмета, или «m»:

а = F/m

Следует уточнить, что данная формула может существовать только в том случае, если равнодействующая всех сил не меньше и не равна нулю. Применяется закон только относительно тел, которые двигаются со скоростью меньше световой.

Литература

• Спасский Б. И.. История физики. М., «Высшая школа», 1977.
• Crowell, Benjamin (2011), Light and Matter (2011, Light and Matter), especially at Section 4.2, Newton’s First Law, Section 4.3, Newton’s Second Law, and Section 5.1, Newton’s Third Law.
• Feynman, R. P. (англ.)русск.; Leighton, R. B.; Sands, M. The Feynman Lectures on Physics (неопр.). — 2nd. — Pearson/Addison-Wesley, 2005. — Т. Vol. 1. — ISBN 0-8053-9049-9.
• Fowles, G. R.; Cassiday, G. L. Analytical Mechanics (неопр.). — 6th. — Saunders College Publishing (англ.)русск., 1999. — ISBN 0-03-022317-2.
• Likins, Peter W. (англ.)русск.. Elements of Engineering Mechanics (неопр.). — McGraw-Hill Education, 1973. — ISBN 0-07-037852-5.
• Marion; Jerry; Thornton, Stephen. Classical Dynamics of Particles and Systems (англ.). — Harcourt College Publishers, 1995. — ISBN 0-03-097302-3.
• Newton, Isaac, «Mathematical Principles of Natural Philosophy», 1729 English translation based on 3rd Latin edition (1726), volume 1, containing Book 1, especially at the section Axioms or Laws of Motion, starting page 19.
• Newton, Isaac, «Mathematical Principles of Natural Philosophy», 1729 English translation based on 3rd Latin edition (1726), volume 2, containing Books 2 & 3.
• Thomson, W (Lord Kelvin), and Tait, P G, (1867), Treatise on natural philosophy, volume 1, especially at Section 242, Newton’s laws of motion.

Вводная информация

Впервые три закона Иссак Ньютон описал в труде «Математические начала натуральной философии» (1867 год), в котором были подробно изложены не только собственные выводы ученого, но все знания по этой теме открытые другими философами и математиками. Таким образом, труд стал фундаментальным в истории механики, а позднее и физики. В нем рассмотрены перемещение и взаимодействие массивных тел.

Каждое утверждение освещает одну из сфер взаимодействия и перемещения предметов в природе, правда обращение к ним было несколько упразднено Ньютоном, и они были приняты как точки без определенного размера (математические).

Именно это упрощение позволило проигнорировать естественные физические явления: воздушное сопротивление, трение, температуру или другие физические показатели объекта.

Полученные данные могли быть описаны только по времени, массе или длине. Именно из-за этого формулировки Ньютона обеспечивают лишь подходящие, но приближенные значения, которые нельзя использовать для описания точной реакции крупных или изменяемых по форме объектов.

Перемещение массивных предметов, которые участвуют в определениях, принято исчислять в инерциальной системе отсчета, представленной в виде системы координат из трех измерений, и при этом она не увеличивает свою скорость и не оборачивается вокруг своей оси.

Ее часто называют системой отсчета Ньютона, но при этом ученый никогда не создавал и не использовал подобной системы, а использовал нерациональную. Именно в этой системе тела могут двигаться так, как описывает это Ньютон.

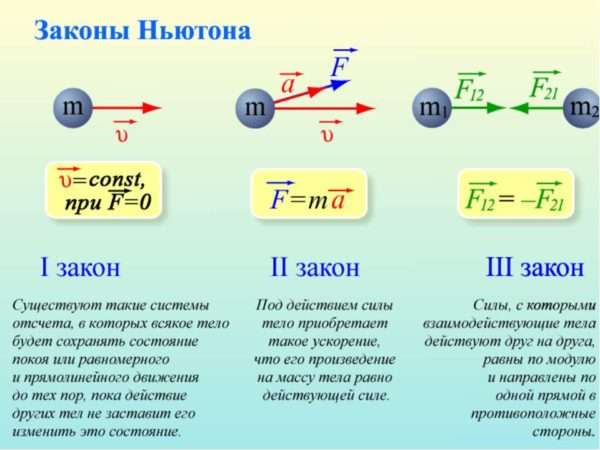
Кратко о законах Ньютона

Первый закон Ньютона

1. Формулировка. В наше время встречаются несколько формулировок, вот одна из самых современных: «Существуют такие инерциальные системы отсчёта, относительно которых тело, если на него не действуют другие силы (либо действие других сил компенсируется), находится в покое либо движется равномерно и прямолинейно». Этот закон иногда называют Законом инерции.
2. Трактовка. Если описать это утверждение простыми словами, то можно увидеть, что всё достаточно просто: если какое-то тело находится в покое относительно чего-либо, то оно и будет оставаться в покое до тех пор, пока на него не подействует какой-либо предмет. То же самое, если тело движется равномерно прямолинейно, то оно будет продолжать так двигаться, пока на него не подействует какая-либо сила. До Ньютона его открыл Галилео Галилей, но он не совсем точно его описал. Теперь осталось только разобраться, что такое инерциальные системы отсчёта. Проще говоря, это такая система, для которой выполняется Первый закон Ньютона.
3. Пример действия. Представьте себе парашютиста, который движется прямолинейно равномерно к Земле. Это будет продолжаться до тех пор, пока притяжение к поверхности Земли будет компенсироваться сопротивлением воздуха. Если же сопротивление станет меньше либо больше, то тогда на тело начнёт действовать сила притяжения, и оно станет двигаться прямолинейно равноускоренно.
4. История открытия. Существует легенда об открытии этого утверждения. Когда-то Ньютон сидел под деревом, и рядом с ним упало яблоко. Это подтолкнуло его на размышления о том, почему яблоко упало перпендикулярно земле, каковы были причины данного явления. По крайней мере, так описывал этот эпизод знаменитый биограф Уильям Стьюкли.
5. Формулы у него нет.

Второй закон Ньютона

Он описывает поведение тела при действии на него других объектов. Что с ним происходит, как он начинает двигаться и прочее.

1. Формулировка. «В инерциальных системах отсчёта ускорение тела с постоянной массой прямо пропорционально равнодействующей всех сил и обратно пропорционально его массе».
2. Формула. Математическое описание этого утверждения такое: а = F/m, где a — это ускорение, F — равнодействующая всех сил, приложенных к телу, m — масса тела.
3. Трактовка. Из формулы мы видим, что ускорение тела зависит от силы, приложенной к этому телу, и массы. А также можно увидеть, что чем больше равнодействующая всех сил, то тем больше ускорение, и чем больше масса тела, тем ускорение меньше. Говоря простым языком, если равнодействующая всех сил не равна нулю и не меньше нуля, то выполняется данное утверждение. Можно сказать ещё проще, если на тело действует сила, то оно приобретает ускорение.
4. Пример действия. Возьмём бейсбольную биту и мяч. Если ударить битой по мячу, и удар будет сильнее действия всех других сил, то мяч приобретёт ускорение равное отношению равнодействующей всех сил к массе.

Третий закон Ньютона

1. Формулировка. «Тела взаимодействуют друг на друга с силами одинаковой природы, направленными вдоль прямой, которая соединяет центры масс этих тел, а силы равны по модулю и разнонаправленны».
2. Трактовка. Это значит, что на каждое действие есть своё противодействие.
3. Пример действия. Более понятно это можно рассмотреть на таком примере: представьте пушку, из которой стреляют ядром. Ядро будет действовать на пушку с той же силой, с какой пушка вытолкала ядро. Поэтому при выстреле пушка откатится чуть-чуть назад, это происходит из-за того, что размеры пушки и ядра разные. Примерно то же самое происходит и при падении яблока на землю. Земля действует на яблоко с некой силой и яблоко тоже действует на Землю. Только из-за того, что масса Земли в миллионы раз больше яблока этого действия не видно. Еще один пример действия Третьего закона для закрепления усвоенного. Возьмём довольно сложный пример: притяжение планет. Луна вертится вокруг Земли благодаря тому, что она притягивается к Земле, но по Третьему закону Ньютона Луна тоже притягивает Землю к себе. Однако, из-за того, что их массы разные, Луна не может притянуть Землю, но у неё получается вызвать отливы и приливы в морях и океанах.
4. Формула. Математически это утверждение можно записать так: F1 = -F2, где F1 — это сила, с которой первое тело действует на второе, а F2 — сила, с которой второе тело действует на первое.

Третий закон Ньютона.

У каждого из нас своя средняя скорость выполнения чего-либо. Ваш уровень продуктивности и эффективности — это равновесие продуктивности и непродуктивности сил в вашей жизни.

Что такое силы продуктивности и непродуктивности?

Силы продуктивности — это сосредоточенность, позитивный настрой и мотивация. А силы непродуктивности — это стресс, недосып и попытки делать десять дел сразу.

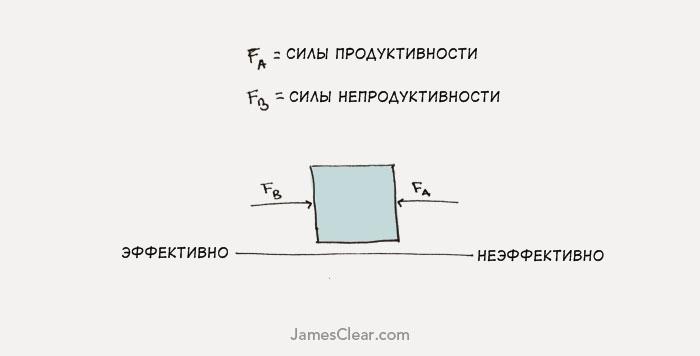
Если вы хотите стать более эффективными и продуктивными, у вас есть два варианта:

1. Приложить больше усилий, то есть увеличить количество силы. Вы поднапряжётесь, выпьете ещё чашку кофе и будете больше работать.

Очевидно, что это будет действовать лишь до тех пор, пока вы не перегорите. Увеличение силы может неплохо сработать, но лишь на короткий период.

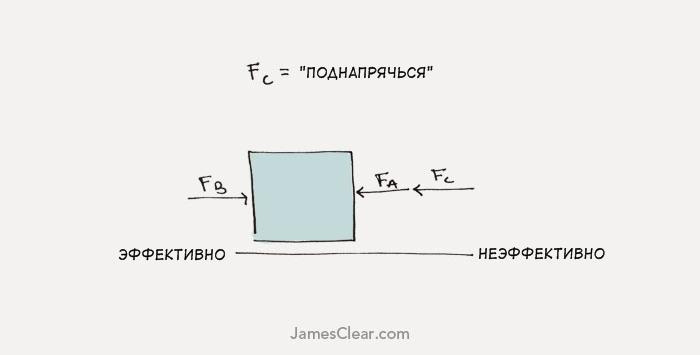
2. Устранить противодействующие силы. Упростить свою жизнь, научиться говорить «нет», уменьшить количество обязанностей.

Иными словами, устранить всё, что вас сдерживает. Избавившись от противодействующих сил, вы увидите, что теперь ваших усилий (тех же самых, не увеличенных!) хватает, чтобы выполнять гораздо больший объём работы.

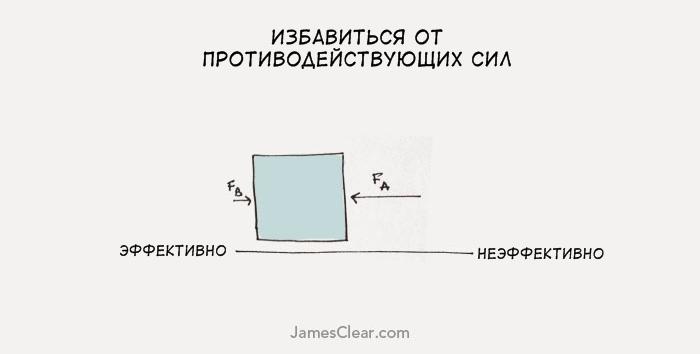
Второй вариант — гораздо проще и результативнее. Но большинство людей инстинктивно выбирает первый, потому что не задумывается о законах Ньютона.

Сколько законов у Ньютона и о чем они

Вокруг нас ежедневно происходит масса удивительных и невероятных вещей, не кажущихся нам таковыми лишь благодаря школьной программе и полученным нами знаниям. Еще несколько тысяч лет назад люди задавались вопросами, многие из которых нашли свои рациональные ответы. Исаак Ньютон сделал огромный прорыв в области классической механики, благодаря чему и вошел в историю.

Классическая механика является наукой о движении материальных тел и взаимодействии между ними. Сколько законов Ньютона легли в ядро классической механики? Всего три — основополагающих и постулирующих всю эту область физики. Они не просто так родились в голове великого ученого. Это совокупность знаний, накопленных тысячелетними наблюдениями, классифицированных Галилеем и сформулированных Ньютоном.

Третий закон Ньютона

Основная статья: Третий закон Ньютона

Этот закон описывает, как взаимодействуют две материальные точки. Пусть имеется замкнутая система, состоящая из двух материальных точек, в которой первая точка может действовать на вторую с некоторой силой F→1→2{\displaystyle {\vec {F}}_{1\to 2}}, а вторая — на первую с силой F→2→1{\displaystyle {\vec {F}}_{2\to 1}}. Третий закон Ньютона утверждает: сила действия F→1→2{\displaystyle {\vec {F}}_{1\to 2}} равна по модулю и противоположна по направлению силе противодействия F→2→1{\displaystyle {\vec {F}}_{2\to 1}}.

Третий закон Ньютона является следствием однородности, изотропности и зеркальной симметрии пространства.

Третий закон Ньютона, как и остальные законы ньютоновской динамики, даёт практически верные результаты лишь только тогда, когда скорости всех тел рассматриваемой системы пренебрежимо малы по сравнению со скоростью распространения взаимодействий (скоростью света).

Современная формулировка

Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно.

Историческая формулировка

Ньютон дал следующую формулировку закона:

Для силы Лоренца третий закон Ньютона не выполняется. Лишь переформулировав его как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость.

Первый закон Ньютона

Барабанную дробь, пожалуйста! Законы Ньютона описывают силы и движение, а его первый закон гласит: “Объект находится в состоянии равновесия или прямолинейном движении с постоянной скоростью, если не подвергается внешнему воздействию”. Нужен перевод? Если вы не прилагаете силу к объекту в покое или “постоянном” движении, то он останется в покое или таком же движении по прямой. Причем вечно!

Например, при игре в хоккей шайба после удара движется к воротам по прямой, скользя по льду почти без трения. В случае удачи соперник не сможет зацепить шайбу своей клюшкой, т.е. не сможет изменить “постоянное” движение шайбы по прямой (и воспрепятствовать голу).

Первый закон Ньютона утверждает лишь то, что единственным способом изменения движения является приложение внешней силы. Иначе говоря, сила является причиной движения. Кроме того, он гласит, что движущийся объект стремится оставаться в движении, что приводит к идее инерции.

Поддерживаем движение: инерция и масса

Инерция — это естественная тенденция объекта оставаться в покое или в движении с постоянной скоростью вдоль прямой линии. Инерция вызвана массой, а масса объекта является мерой инерции. Чтобы привести объект в движение, т.е. изменить его текущее состояние движения, необходимо приложить силу для преодоления инерции.

Представьте себе причал с маленькой шлюпкой и большим танкером с нефтью. Если попробовать толкнуть их ногой, то поведение этих судов будет разным. Шлюпка заскользит по водной глади, а танкер едва “вздрогнет” (да и для этого потребуется невероятно сильный толчок!). Дело в том, что они обладают совершенно разной массой и потому разной инерцией. В ответ на одинаковую силу объект с малой массой (и малой инерцией) ускорится в большей мере, чем объект с малой массой и большей инерцией.

Инерция, т.е. тенденция массы сохранять неизменность текущего состояния движения, иногда может представлять проблему. Например, в рефрижераторе тяжелые туши мороженного мяса подвешены к потолку кузова. Если рефрижератор войдет в крутой поворот на большой скорости, то туши по инерции начнут раскачиваться, как маятники, и их трудно будет остановить. Часто неопытные водители не учитывают инерцию туш мяса, и это приводит к печальным последствиям, например к опрокидыванию машины.

Измеряем массу

В разных системах измерения физических величин для указания массы (а значит, и инерции) используются разные единицы. В системе СГС используется грамм, а в системе СИ — килограмм, который содержит 1000 грамм.

А какая единица используется в Английской системе мер на основе фута-фунта- дюйма? Наберитесь мужества: в ней используется единица “слаг”, которая эквивалентна 14,5939 килограмма.

Форсируем тему

В окружающем нас мире нельзя избежать встречи с силами: силы используются для открытия двери, нажатия клавиш клавиатуры, управления автомобилем, подъема по ступенькам лестницы к Статуе Свободы, вытаскивания кошелька из кармана, разговора и даже для дыхания. Силы незримо присутствует всюду: во время пешеходной прогулки, катании на коньках, пережевывании хот-дога, открывании бутылки или моргании ресниц вашей ненаглядной спутницы. Сила неразрывно связана с движением объектов, а физика помогает понять, как эта связь работает.

Сила — это на самом деле довольно забавная тема. Как и другие физические темы, она кажется сложной только до настоящего знакомства с ней. Как наши старые “друзья”, перемещение, скорость и ускорение (см. главы 3 и 4), сила является вектором, т.е. имеет величину и направление.

Как часто происходит со многими физическими открытиями, Ньютон сначала внимательно наблюдал за поведением объектов, мысленно моделировал его, а затем выразил в математической форме. Зная основные сведения о векторах (которые изложены в главе 4), эта математика не вызовет у вас никаких трудностей.

Примечания

1. ↑ Исаак Ньютон. Математические начала натуральной философии. Перевод с латинского и примечания А. Н. Крылова / под ред. Полака Л. С.. — М.: Наука, 1989. — С. 40—41. — 690 с. — (Классики науки). — 5 000 экз. — ISBN 5-02-000747-1.
2. Тарг С. М. // Физическая энциклопедия : / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 370. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
3. // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 146. — 704 с. — ISBN 5-85270-061-4.
4. // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 2. — С. 145. — ISBN 5-85270-034-7.
5. «Дополнительной характеристикой (по сравнению с геометрическими характеристиками) материальной точки является скалярная величина m — масса материальной точки, которая, вообще говоря, может быть как постоянной, так и переменной величиной. … В классической ньютоновской механике материальная точка обычно моделируется геометрической точкой с присущей ей постоянной массой) являющейся мерой её инерции.» стр. 137 Седов Л. И., Цыпкин А. Г. Основы макроскопических теорий гравитации и электромагнетизма. М: Наука, 1989.
6. Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
7. Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 160. — 720 с. — ISBN 5-211-04244-1. «Аксиома 3.3.1. Масса материальной точки сохраняет своё значение не только во времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий».
8. Журавлёв В. Ф. Основы теоретической механики. — М.: Физматлит, 2001. — С. 9. — 319 с. — ISBN 5-95052-041-3. «Масса полагается постоянной, независящей ни от положения точки в пространстве, ни от времени».
9. Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
10. «В ньютоновской механике… m=const и dp/dt=ma». Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с..
11. Зоммерфельд А. Механика = Sommerfeld A. Mechanik. Zweite, revidierte auflage, 1944. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 45—46. — 368 с. — ISBN 5-93972-051-X.
12. Кильчевский Н. А. Курс теоретической механики. Том 1. — М.: Наука, 1977. 480 с.
13. Жирнов Н. И. Классическая механика. — Серия: учебное пособие для студентов физико-математических факультетов педагогических институтов. — М., Просвещение, 1980. — Тираж 28 000 экз. — с. 38
14. Тютин И. В. Симметрия в физике элементарных частиц. Часть 1. Пространственно-временные симметрии. // Соросовский образовательный журнал, 1996, № 5, с. 65
15. Сивухин Д. В. Общий курс физики. Механика. — М., Наука, 1979. — Тираж 50 000 экз. — с. 85
16. ↑ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — 320 с.
17. Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
18. Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 282. — 416 с. — ISBN 5-06-003117-9.
19. ↑ Тарг С. М. // Физическая энциклопедия : / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 494—495. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
20. ↑
21. «„Силы инерции“ — не силы». Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 21. — 46 с.
22. Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 82. — 368 с. — ISBN 5-93972-051-X.
23. Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
24. Фейнман Р., Лейтон Р., Сэндс М. Выпуск 1. Современная наука о природе. Законы механики // Фейнмановские лекции по физике. — М.: «Мир», 1965. — С. 225.
25. Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 186—197;
26. ↑ Кузнецов Б. Г. Генезис механического объяснения физических явлений и идеи картезианской физики // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 160—161, 169—170, 177;