Примеры решений задач с помощью второго замечательного предела

Ответы@Mail.Ru: А когда считаешь предел и получается ноль умножить на бесконечность

Мистер Бонд, прочтите первый том «Курса дифференциального и интегрального исчисления» Г. М. Фихтенгольца. Ноль * Бесконечность — это неопределенность. Она сводится к неопределенности типа 0 / 0 или Бесконечность / Бесконечность, которые дальше можно раскрыть, например, применяя правила Лопиталя.
Не хотите открывать Фихтенгольца — суньтесь в Яндекс. Вот ссылочка первая же по запросу «Неопределенность, Правило Лопиталя» <a rel=»nofollow» href=»http://www.mathelp.spb.ru/book1/lopital.htm» target=»_blank»>http://www.mathelp.spb.ru/book1/lopital.htm</a>
Успехов в решении! И не забывайте о том, что Джеймс Бонд всегда находил решения самых трудных задач.

к сожалению только ноль…

А что у нас «ноль»? Ноль величина абстрактная и в природе не имеющая места быть вообще.

нуль. Нуль деленная на беск-ть=неопред-ть.

не слушай троечников — неопределенность, разумеется! И может получиться любое число в результате.

Иногда так хочется,чтоб ноль стал бесконечностью…

Это вы предел не доразложили. Непонятно какой ноль и какая бесконечность.
Например:
1. Lnx/x при x стремящемся к бесконечности — 0
2. e^x/x при x стремящемся к бесконечности — бесконечность
3. sin2x/x при x стремящемся к 0 равно 2
Поэтому, прежде чем считать предел типа f(x)/g(x) при x стремящемся к x0 надо провести разложение в окрестности x0 обоих функций и после сокращения в числителе или знаменателе у вас останется константа — а далее все просто.

Это неопределенность.

Это неопределенность. Одна сорокомиллионная — это практически ноль, а сорок миллионов — почти бесконечность,их перемножить, что получится?Если мы не знаем точно о сорока миллионах или о восьмидесяти идет речь? Неопределенность.

Это неопределенность типа ноль умножить на бесконечность.

Сколько раз ни складывай ноль с нулем, ноль никогда не сдвинется с места, даже если бесконечное число раз. Это очевидно, поэтому результат всегда равен нулю.
Другие числа могут получиться, если считать предел произведения функций, одна из которых стремится к нулю, а другая к бесконечности, в этом случае все зависит от их скоростей стремления к нулю или к бесконечности.

0 на бесконечность умножать нельзя
т. к возьмем 0 0/0=бесконечность
А 1/0= тоже бесконечность любое число даже 0 деленное на 0 будет бесконечность и число умножая на бесконечность будет неопределимость бесконечностью не имеет значения поэтому 0 * бесконечность нельзя а 0 на себя можно

Неопределённость «бесконечность минус бесконечность»

Популярная неопределённость  устраняется тремя распространёнными способами:

– приведением выражения под знаком предела к общему знаменателю;

– умножением/делением на сопряжённое выражение;

– преобразованием логарифмов.

Рассмотрим первый случай, о котором я ещё не рассказывал:

Пример 9

Вычислить предел

В данном пределе имеет место неопределённость , и общий алгоритм решения незамысловат: необходимо привести выражение к общему знаменателю, а затем попытаться что-нибудь сократить:

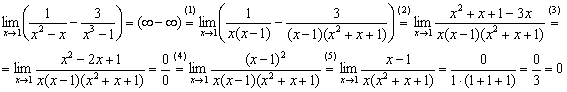
(1) Раскладываем знаменатели на множители: в первом знаменателе выносим «икс» за скобки, во втором знаменателе используем формулу разности кубов . Данный шаг можно было пропустить, но этим пришлось бы заниматься потом, и, на мой взгляд, разложение на множители удобнее провести сразу же.

(2) Приводим выражение к общему знаменателю.

(3) Приводим подобные слагаемые в числителе. Неопределённость  трансформировалась в неопределённость , которая стандартно раскрывается разложением числителя и знаменателя на множители.

(4) Знаменатель уже разложен на множители. Раскладываем на множители числитель, в данном случае использована формула .

(5) Сокращаем числитель и знаменатель на , устраняя неопределённость.

Как видите, новизны-то особой и нет.

Аналогичное задание для самостоятельного решения:

Пример 10

Вычислить предел

Решение и ответ в конце урока

Второй вид пределов с неопределённостью  представляет собой разность, в которой присутствуют два или один корень:

Пример 11

Вычислить предел

Каноничный образец. Метод решения подробно разобран на уроке Пределы. Примеры решений. Необходимо умножить и разделить на сопряженное выражение, чтобы потом воспользоваться формулой

Умножим и разделим на сопряженное выражение:

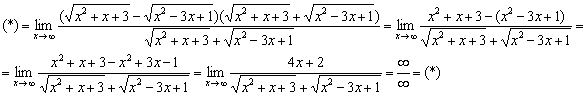
Неопределённость  превратилась в неопределённость . Узнаёте? Такие семечки мы грызли в первом разделе данного урока.

Числитель и знаменатель одного порядка роста, а значит, предел равен конечному числу. Разделим числитель и знаменатель на :

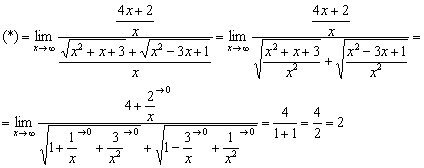
Не редкость, когда в разности всего один корень, но это не меняет алгоритма решения:

Пример 12

Вычислить предел

Пример 13

Вычислить предел

Это пара коротких примеров для самостоятельного решения.

Следует отметить, что пределы рассмотренного типа не обязаны равняться конечному числу, вполне может получиться и бесконечность, причём, как «плюс», так и «минус». Кстати, в примере №13 можно посмотреть на порядок роста членов, чтобы сразу выяснить ответ 😉

Иногда на практике встречаются пределы-«обманки», в которых неопределённости «бесконечность минус бесконечность» нет вообще, вот простейший пример:

Таким образом, будьте предельно внимательны: перед решением предела необходимо убедиться, что неопределённость  действительно есть!

В заключительной части статьи вернёмся к незаслуженно забытым замечательным пределам, где рассмотрим, в том числе, третий тип пределов с неопределённостью .

Кодировка символа бесконечности

Платформа	Сочетание клавиш	Описание
Компьютер с Windows	Alt + 236	удерживая клавишу ALT, набрать 236 на цифровой клавиатуре;
Apple macOS	Option + 5	удерживая клавишу Option, нажать 5;
Microsoft word и Microsoft excel	Вставка → Символ → Другие символы → Код знака:221E Скопировать ∞ Ctrl+C → Ctrl+V Alt + 236	слева будет «Вставка», в правом верхнем углу будет «Символ» Тату анубис: значение, эскизы и 70+ фото оригинальных решений скопировать знак здесь ∞ и вставить в документ удерживая клавишу ALT, набрать 236 на цифровой клавиатуре;
Вебсайт	Ctrl+C → Ctrl+V	Скопировать знак здесь ∞ и вставить его на свою веб-страницу
Код для ВК	‎&‎#9854
Facebook, инстаграм и т. д.	Ctrl+C → Ctrl+V	Скопировать знак здесь ∞
Символ бесконечности HTML	&‎#8734
Юникод	U+221E
CSS-код	\221E
ASCII	236
LaTeX и MATLAB	\infty

Виды и правила раскрытия неопределенностей (Таблица)

Вид неопределенности

Правило раскрытия

1.       

1.1. Чтобы раскрыть неопределенность вида ,

заданную отношением двух многочленов, надо и числитель и знаменатель почленно разделить на переменную величину в наибольшей степени.

1.2. Для раскрытия неопределенности вида ,

заданную отношением иррациональных функций, надо и числитель и знаменатель почленно разделить на переменную величину в наибольшей степени с учетом степеней корней.

2.        

2.1. Для того, чтобы определить предел дробно-рациональной функции в случае, когда при

x → a числитель и знаменатель дроби имеют пределы, равные  нулю, надо числитель и знаменатель дроби разделить на x — a и перейти к пределу. Если и после этого числитель и знаменатель новой дроби имеют пределы, равные  нулю при x → a, то надо произвести повторное деление на x — a.

2.2. Чтобы раскрыть неопределенность вида ,

в которой числитель или знаменатель иррациональны, следует надлежащим образом избавиться от иррациональности, умножив и числитель и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.

В случае квадратных корней и числитель и знаменатель дроби умножаются на сопряженное выражение тому, которое содержит иррациональность и применяется формула

a2 – b2 = (a – b)(a + b) .

В случае кубических корней и числитель и знаменатель дроби умножаются на неполный квадрат суммы или разности и применяется формула

a3 ± b3 = (a ± b)(a2 ± ab + b

2).

3.     

3.1. Неопределенность вида ,

получающаяся в результате алгебраической суммы иррациональных выражений, устраняется или приводится к типу 1 путем домножения и деления на одно и то же выражение, приводящее к формулам сокращенного умножения.

В случае квадратных корней разность домножается на сопряженное выражение и применяется формула a2 – b2 = (a – b)(a + b) .

В случае кубических корней функция домножается на неполный квадрат суммы или разности и применяется формула a3 ± b3 = (a ± b)(a2 ± ab + b2).

3.2. Неопределенность вида ,

получающаяся в результате алгебраической суммы двух дробей, устраняется или сводится к типу 2  путем приведения дробей к общему знаменателю.

Пусть:

, .

Тогда:

4. Замечательные пределы

 4.1. Первый замечательный предел  (неопределенность ).

В случае, когда под знаком предела стоят тригонометрические функции, дающие неопределенность , используется первый замечательный предел:

Его различные формы:      ,     ,     ,

  ,          ,

  ,          .

4.2. Второй замечательный предел (неопределенность ):   

Его различные формы:

,    ,      , ,    

5.       

5.1. Неопределенность вида  

сводится либо к неопределенности типа 1 , либо к неопределенности типа 2  путем перемещения в знаменатель одного из сомножителей.

Пусть

, .

Тогда:

Ответы@Mail.Ru: Бесконечность в степени бесконечность

Два примера показывают, что здесь нет неопределенности:
n^n —&gt; oo, если n —&gt; +oo,
n^(-n) —&gt; 0, если n —&gt; +oo.
В общем случае тоже либо 0, либо бесконечность.

Смотри, бывает «минус бесконечность». Любое конечное число в степени «минус бесконечность» — это будет ноль.
Поэтому если у тебя не определён знак бесконечности — то это неопределённость.

Любое число в степени бесконечность даст бесконечность. А бесконечность в степени бесконечность и подавно.
Уточняю. Число более 1)).

Ясно, что бесконечность! Что-то вроде континуума по сравнению со счётным множеством.
А вот «единица в степени бесконечность» — это условное обозначение неопределённости!

Это бесконечность. Потому что бесконечность в любой степени, кроме нулевой — всегда бесконечность

Есть классификация бесконечностей, введенная Георгом Кантором, но для вычисления пределов это неважно

Бесконечности в числовом понимании — предельные понятия.
Таким макаром, вопрос сводится к следующему: «чему равен lim xn^yn, если lim xn = бесконечность, lim yn = бесконечность».
Можно доказать этот факт и увидеть, что получится снова бесконечность. Впрочем, доказательство может быть нетривиальным.

Примечания

1. ↑
2. Scott, Joseph Frederick (1981), (2 ed.), American Mathematical Society, с. 24, ISBN 0-8284-0314-7
3. Clegg, Brian (2003), A brief history of infinity: the quest to think the unthinkable, Robinson, ISBN 9781841196503
4. Zboray, Ronald J. & Zboray, Mary Saracino (2000), A handbook for the study of book history in the United States, Center for the Book, Library of Congress, с. 49, ISBN 9780844410159
5. O’Flaherty, Wendy Doniger (1986), , University of Chicago Press, с. 243, ISBN 9780226618555. The book also features this image on its cover.
6. Toker, Leona (1989), , Cornell University Press, с. 159, ISBN 9780801422119
7. Healy, Donald T. & Orenski, Peter J. (2003), Native American Flags, University of Oklahoma Press, с. 284, ISBN 978-0-8061-3556-4

Метод мнимых единиц Править

Метод, предложенный канадскими учёными. Понятно, что $ \frac{-1}{1}=\frac{1}{-1} $. Значит, $ \sqrt {\frac{-1}{1}} = \sqrt {\frac{1}{-1}} $. Значит, $ \frac{\sqrt {-1}}{\sqrt {1}}=\frac{\sqrt {1}}{\sqrt {-1}} $. Так как $ \sqrt {-1}=i $, запишем равенство следующим образом: $ \frac{i}{1}=\frac{1}{i} $. Разделим обе части на 2, получим $ \frac{i}{2}=\frac{1}{2i} $. Далее, прибавим к обеим частям равенства выражение $ \frac{3}{2i} $, получим $ \frac{i}{2}+\frac{3}{2i}=\frac{1}{2i}+\frac{3}{2i} $. Теперь умножим обе части на $ i $, получим $ i(\frac{i}{2}+\frac{3}{2i})=i(\frac{1}{2i}+\frac{3}{2i}) $, раскроем скобки: $ \frac{i^2}{2}+\frac{3i}{2i}=\frac{i}{2i}+\frac{3i}{2i} $. Так как $ i^2=-1 $, получаем $ \frac{-1}{2}+\frac{3}{2}=\frac{1}{2}+\frac{3}{2} $. Посчитав, получим, что $ 1=2 $, а отняв $ 1 $, найдем требуемое равенство: $ 0=1 $.

На самом деле $ \sqrt {\frac{1}{-1}}\neq\frac{\sqrt {1}}{\sqrt {-1}} $. Выражение «корень из дроби есть корень из числителя делённый на корень из знаменателя» верно, если неположителен числтель или положителен знаменатель.

И вообще учите МАТЕМАТИКУ, а не тратьте время на софизмы!

История знака бесконечности

Символ бесконечности (∞) был создан Джоном Уоллисом, английским математиком в 1655 году. Однако само понятие бесконечности было задокументировано ещё с древнегреческих времён.

Учение «апейрон» философа Анаксимандра

Самые ранние записи идеи бесконечности датируются ещё 610 – 546 гг.

Древнегреческий философ Анаксимандр полагал, что Вселенная возникла из апейрона (вечное движение времени), на греческом это означает «бесконечный» или «неограниченный».

Философия Анаксимандра заключалась в том, что апейрон приводит к тому, что по мере возникновения мира противоположности (такие как жар и холод, ночь и день) отделяются друг от друга.

Изображение змеи/дракона Уроборос

Посредством изображения Уроборос (змеи, которая поедала свой собственный хвост) мир искусства передал идею, похожую на бесконечность. Этот образ считается самым старым и известным изображением бесконечности. Уроборос был у греков в 400 году нашей эры, но символ фактически восходит ещё к Древнему Египту, к 14 веку до нашей эры.

Уроборос

Иногда Уроборос изображается как две переплетённые змеи, или как змея в форме восьмёрки, или в форме круга. Зачастую это изображение интерпретируется как цикл жизни и смерти, но существуют и другие толкования.

Использование

Символ долговечной бумаги в переплётном деле

В математике символ бесконечности используется чаще всего для выражения потенциальной бесконечности, а не обозначения каких-то реальных бесконечно больших величин. Например, в математическом обозначении предела:

∑i=∞12i=limx→∞2x−12x−1=2{\displaystyle \sum _{i=0}^{\infty }{\frac {1}{2^{i}}}=\lim _{x\to \infty }{\frac {2^{x}-1}{2^{x-1}}}=2},

знак бесконечности можно условно интерпретировать в том смысле, что переменная достигает сколь угодно больших значений (стремится к бесконечности), но не принимает значения, равного бесконечности.

В топологии символом бесконечности обозначается дополнительная точка, которая вводится при одноточечной компактификации Александрова. Аналогично, в комплексном анализе и проективной геометрии символ ∞{\displaystyle \infty } обозначает .

Но в областях математики, в которых возникает необходимость сравнивать и различать между различными типами бесконечности, для конкретных бесконечных величин вместо символа ∞{\displaystyle \infty } используются иные обозначения. Например, в теории множеств, бесконечное кардинальное число множества натуральных чисел (мощность множества всех натуральных чисел) обозначается символом ℵ{\displaystyle \aleph _{0}} (читается «алеф-нуль»), бесконечное кардинальное число множества счётных порядковых чисел обозначается ℵ1{\displaystyle \aleph _{1}}, при этом ℵ<ℵ1{\displaystyle \aleph _{0}<\aleph _{1}}. См. Иерархия алефов.

В других отраслях символ бесконечности может иметь другой смысл; например, в переплётном деле он используется для указания, что книга напечатана на долговечной бумаге.

Что-то там не то[править]

Может там должно быть
limx→∞1x=limx→∞1⋅1x−1{\displaystyle \lim _{x\to \infty }{1^{x}}=\lim _{x\to \infty }{1\cdot 1^{x-1}}} ? —Alokrot 10:09, апреля 12, 2010 (UTC)

Да, действительно. Только limx→∞1x=limx→∞x⋅1x−1{\displaystyle \lim _{x\to \infty }{1^{x}}=\lim _{x\to \infty }{x\cdot 1^{x-1}}}. — José Monteiro 13:20, апреля 12, 2010 (UTC)

Не верю!!! 1x{\displaystyle 1^{x}} — это почти единица, а вот x⋅1x−1{\displaystyle x\cdot 1^{x-1}} — это уже много. Там с логарифмами, наверное, надо побаловаться. —Alokrot 10:11, апреля 13, 2010 (UTC)

Правило Лопиталя: limx→a+f(x)g(x)=limx→a+f′(x)g′(x){\displaystyle \lim _{x\to a+}{\frac {f(x)}{g(x)}}=\lim _{x\to a+}{\frac {f'(x)}{g'(x)}}}. Но т.к. g(x)=1{\displaystyle g(x)=1}, т.е. число, то берём g′(x)=g(x)=1.{\displaystyle g'(x)=g(x)=1.} a+{\displaystyle a+} в данном случае — это ∞{\displaystyle \infty }. А где тут могут быть логарифмы? — José Monteiro 12:27, апреля 13, 2010 (UTC)

Проба объяснения[править]

Задача 1∞{\displaystyle 1^{\infty }} правильно уточняется в виде Невозможно разобрать выражение (неизвестная функция «\substack»): {\displaystyle \lim_{\substack{ x\to 1 \\ f(x)\to +\infty }}{x^{f(x)}}}
. Тогда можно написать, что

Невозможно разобрать выражение (неизвестная функция «\substack»): {\displaystyle \lim_{\substack{ x\to 1 \\ f(x)\to +\infty }}{x^{f(x)}} = \lim_{\substack{ x\to 1 \\ f(x)\to +\infty }}e^{\ln {x^{f(x)}}} = \lim_{\substack{ x\to 1 \\ f(x)\to +\infty }}e^{f(x) \cdot \ln x}}

Значение последнего выражения фактически зависит от

Невозможно разобрать выражение (неизвестная функция «\substack»): {\displaystyle \lim_{\substack{ x\to 1 \\ f(x)\to +\infty }}{f(x) \cdot \ln x}}
— а значит сводится к неопределённости вида ∞⋅{\displaystyle \infty \cdot 0}

—Alokrot 02:06, апреля 20, 2010 (UTC)

Первое: я полагаю, что во втором пределе Невозможно разобрать выражение (неизвестная функция «\substack»): {\displaystyle \lim_{\substack{ x\to 1 \\ f(x)\to +\infty }}e^{\ln {x^{f(x)}}}}
выражение eln⁡x{\displaystyle e^{\ln {x}}} следует взять в скобки, т.е. должно быть Невозможно разобрать выражение (неизвестная функция «\substack»): {\displaystyle \lim_{\substack{ x\to 1 \\ f(x)\to +\infty }}(e^{\ln {x}})^{^{f(x)}}}
.
Второе: выходит, задача усложняется новыми неопределённостями ⋅∞{\displaystyle 0\cdot \infty } и e∞{\displaystyle e^{\infty }}. Как быть с ними? Ведь их тоже придётся доказывать, что может сделать статью громоздкой. — José Monteiro 12:21, апреля 20, 2010 (UTC)
Ну я здесь, если честно, ни черта не понял, ну да ладно. Суть в том, что статья может быть сколь угодно большого размера, если требуется. Не стоит пугаться громоздскости серьёзной статьи. ГиМЦ-Д 15:08, апреля 20, 2010 (UTC)
Я не пугаюсь громоздкости статьи, просто мы отойдём от темы и, в лучшем случае придётся это рассматривать как стимул к созданию новых похожих одна на другую статей. — José Monteiro 14:13, апреля 21, 2010 (UTC)Так эти же формулы равны из-за того, что (xa)b=xb⋅a{\displaystyle {(x^{a})}^{b}=x^{b\cdot a}}.

e∞{\displaystyle e^{\infty }} там вроде бы нет — есть «e» в степени «неопределённость». А вот от неопределённости ⋅∞{\displaystyle 0\cdot \infty } уже невозможно избавиться (разве что свести к неопределённостям ноль-на-ноль или бесконечность-на-бесконечность). Фактически, наша исходная неопределёность зависит от соотношения «скоростей», с которыми стремятся f(x) к бесконечности и ln⁡x{\displaystyle \ln x} к нулю. Например, если f(x)=1ln⁡x{\displaystyle f(x)=1/\ln x}, то для случая limx→1x1ln⁡x{\displaystyle \lim _{x\to 1}{x^{1/\ln x}}} можно будет сказать, что это выражение limx→1x1ln⁡x=e1=e{\displaystyle \lim _{x\to 1}{x^{1/\ln x}}=e^{1}=e}

—Alokrot 16:17, апреля 20, 2010 (UTC)

(xa)b=xb⋅a{\displaystyle {(x^{a})}^{b}=x^{b\cdot a}}, но я обратил внимание, что были опущены скобки, а, насколько мне известно, (xa)b≠xab{\displaystyle ({x^{a}})^{b}\neq {{x^{a}}^{b}}}.
Насчёт e∞{\displaystyle e^{\infty }}, я немного ошибся, спутал формулы.
А почему Вы считаете, что limx→1x1ln⁡x=e1=e{\displaystyle \lim _{x\to 1}{x^{1/\ln x}}=e^{1}=e}? Кстати, если это правильное выражение, то Вы получили третий вариант ответа на вопрос, заложенный в теме статьи. — José Monteiro 14:13, апреля 21, 2010 (UTC)
 1.  А-а, понятно — я написал Невозможно разобрать выражение (неизвестная функция «\substack»): {\displaystyle \lim_{\substack{ x\to 1 \\ f(x)\to +\infty }}e^{\ln {x^{f(x)}}}}
подразумевая Невозможно разобрать выражение (неизвестная функция «\substack»): {\displaystyle \lim_{\substack{ x\to 1 \\ f(x)\to +\infty }}e^{\ln (x^{f(x)})}}
.
 3.  limx→1x1ln⁡x=limx→1eln⁡(x1ln⁡x)=limx→1e(1ln⁡x)⋅ln⁡x=e1=e{\displaystyle \lim _{x\to 1}{x^{1/\ln x}}=\lim _{x\to 1}{e^{\ln(x^{1/\ln x})}}=\lim _{x\to 1}{e^{(1/\ln x)\cdot \ln x}}=e^{1}=e}

Только там пределы, похоже, уже не особо и нужны были 😀
Вопросов нет. Выкладывайте, наверное, п.3 в статью. 🙂 — José Monteiro 12:14, апреля 22, 2010 (UTC)

Геометрический метод 1 Править

Равные треугольники

Рассмотрим два треугольника, представленных на рисунке. Площадь первого треугольника равна 60 клеточкам, а площадь второго треугольника, составленного из тех же фигур, что и первый треугольник, равна 58 клеточкам (две чёрные клетки внутри вырезаны). Получается, что $ 58=60 $. Отнимем от обеих частей равенства 58 и разделим на 2, получим $ \frac{58-58}{2}=\frac{60-58}{2} $, то есть $ 0=1 $, что и требовалось доказать.

Это вообще не треугольники. Посмотрим на его составляющие — красный и синий треугольники. Т.к. они являются частью ОДНОЙ стороны большого треугольника, то должны иметь одинаковый «наклон» своих гипотенуз, т.е. одинаковый верхний угол, а значит и одинаковые тангенсы этих углов. Но у красного тангенс 2/5, а у синего 3/7. Следовательно из сторон красного и синего треугольников НЕЛЬЗЯ составить ПРЯМУЮ сторону большого треугольника. Только — ломаную. В левой фигуре боковая сторона будет «сломлена» внутрь, а в правой — наружу. Т.о. фигуры РАЗНЫЕ! Разница их площадей как раз и даст недостачу в 2 кв. см. (Путем подсчета сумм площадей окрашенных мелких фигур, получим, что площадь левой фигуры 59, а правой — 59 + 2 черных квадратика)

Применяемые формулы, свойства и теоремы

Здесь мы рассмотрим примеры решений задач на вычисление пределов, в которых используется второй замечательный предел и его следствия. Ниже перечислены формулы, свойства и теоремы, которые наиболее часто применяются в подобного рода вычислениях.

• Второй замечательный предел и его следствия:,     ,     ,     . Стоит отметить еще одну формулу , где – действительное число.
• свойства экспоненты и натурального логарифма.
• Арифметические свойства предела функции.
• Теоремы о пределе и непрерывности сложной функции.

Здесь мы будем иметь дело со степенно-показательной функцией, у которой основание и показатель являются функциями от некоторой переменной: . Ее удобно представить как экспоненту: . В этой связи полезна следующая лемма.

Лемма о пределе степенно-показательной функции Пусть – функции переменной , имеющие конечные пределы:. Здесь . Тогда.

В случае бесконечных пределов, или когда , мы проводим исследование произведения , применяя свойства пределов бесконечно больших и малых функций.

В случае и , мы имеем неопределенность вида единица в степени бесконечность. Для ее раскрытия используется второй замечательный предел.