Троичная логика

Содержание:

Примечания
Система команд
- Регистры
- Список команд
Теория вероятностей и многозначные логики
История
Литература
Предыстория
Логики
- Логики Клини и Приста
Будущее
Элементы троичных ЭВМ (компьютеров)[править | править код]
- Импульсныеправить | править код
Будущее
Трёхзначные логики
Логики[править | править код]
- Логики Клини и Пристаправить | править код
Функциональный подход
Заключение

Примечания

D. C. Rine (ed.), Computer Science and Multiple-Valued Logic. Theory and Applications. Elsevier, 1977, 548p. ISBN 9780720404067
Брусенцов Н. П. Электромагнитные цифровые устройства с однопроводной передачей трёхзначных сигналов // Магнитные элементы автоматики и вычислительной техники. XIV Всесоюзное совещание (Москва, сентябрь 1972 г.). — Москва: Наука, 1972. — С. 242-244.
↑
(недоступная ссылка). Дата обращения 20 марта 2009.
↑
(недоступная ссылка). Дата обращения 13 ноября 2008.
D.E. Knuth, The Art of Computer Programming — Volume 2: Seminumerical Algorithms, pp. 190—192. Addison-Wesley, 2nd ed., 1980. ISBN 0-201-03822-6.

Система команд

Система команд одноадресная. Представление чисел — с фиксированной запятой, одинарной (9 тритов) и двойной (18 тритов) точности. Прямо адресуемое адресное пространство — 243 ячейки. Обмен информацией между ОЗУ и ЗУ на магнитном барабане осуществляется страницами (зонами) по 54 9-разрядных ячейки.

Формат команды (при печати)

k y₁ y₂ x₁ y₃ y₄,

где

k — признак команды,

y₁—y₄ — девятеричные цифры с симметричной базой,

x — цифра троичной системы с симметричной базой,

y₁y₂ — адрес команды,

x₁ — признак длины ячейки,

y₃y₄ — код операции.

Регистры

регистр команд — 9 разрядов,
регистр номера команды (счётчик команд) C — 5 разрядов,
регистр переадресации УУ F — 5 разрядов,
2 9-разрядных регистра — входной и выходной — в блоке управления вводом-выводом,
регистр АУ R — 18 разрядов,
сумматор АУ s — внутренний формат 19 разрядов, доступно 18 разрядов.

Список команд

Код операции	Название	Вид
3̅3̅	Чтение зоны с барабана в ОЗУ	xy₁y₂ 3̅3̅
3̅0	Чтение с перфоленты в ОЗУ	x 00 3̅0
3̅0	Троичный вывод (печать)	x 03 3̅0
3̅0	Вывод в один столбец	x 03̅ 3̅0
3̅0	Вывод в два столбца	х 01̅ 3̅0
3̅0	Вывод в три столбца	х 01 3̅0
3̅3	Запись из ОЗУ на барабан	ху₁у₂ 3̅3
2̅3	Нормализация	а т 2̅3
2̅0	Сдвиг	а т 2̅0
2̅3	Перенос из s в ОЗУ	а т 2̅3
1̅3	Сложение, F + → F	а т 1̅3
1̅0	Перенос из ОЗУ в F	а т 1̅0
1̅3	Сложение + C → F; F → C	а т 1̅3
2̅3̅	Нормализация	а т 2̅3̅
2̅0	Сдвиг	а т 2̅0
2̅3	Перенос числа из s в ОЗУ	а т 2̅3
1̅3̅	Сложение F + → F	а т 1̅3̅
1̅0	Перенос из ОЗУ в F	а т 1̅0
1̅3	Сложение + C → F; F → C	а т 1̅3
03̅	Перенос из F в ОЗУ	а т 03̅
00	Безусловный переход	а т 00
03	Перенос из C в ОЗУ	а т 03
13̅	Условный переход (УП-1̅)	а т 13̅
10	Условный переход (УП-0)	а т 10
13	Условный переход (УП-1)	а т 13
23̅	Останов машины до нажатия на пульте кнопки Пуск	а т 23̅
20	Логическое поразрядное умножение	а т 20
23	Перенос из ОЗУ в R	а т 23
33̅	Вычитание	а т 33̅
30	Перенос числа из ОЗУ в s	а т 30
33	Сложение	а т 33
43̅	Умножение-1̅	а т 43̅
40	Умножение-0	а т 40
43	Умножение-1	а т 43

Теория вероятностей и многозначные логики

Планковские единицы

Может показаться, что теория вероятностей очень похожа на бесконечнозначную логику: вероятность соответствует истинностному значению (1=истина, 0=ложь), вероятность ненаступления какого-либо события соответствует отрицанию, вероятность одновременного наступления двух событий соответствует конъюнкции, а вероятность наступления хотя бы одного из двух событий соответствует дизъюнкции.

Однако между многозначными логиками и теорией вероятностей есть принципиальное различие: в логиках истинностное значение любой функции целиком определяется истинностным значением её аргументов, в то время как в теории вероятностей вероятность составного события зависит не только от вероятностей входящих в него событий-компонентов, но и от их зависимости друг от друга (что выражается через их условные вероятности).

Это проявляется, в частности, в том, что в теории вероятностей выполняется эквивалент «закона исключённого третьего»: вероятность того, что некоторое событие наступит или не наступит, всегда равна единице, в то время как в многозначных логиках закон исключённого третьего не выполняется.

В теории вероятностей выполняется также эквивалент «закона противоречия»: вероятность того, что некоторое событие одновременно наступит и не наступит, всегда равна 0, в то время как в многозначных логиках закон противоречия не выполняется.

В то же время существует некоторая связь между истинностными значениями вышеописанной бесконечнозначной логики и вероятностями теории вероятностей, а именно:

если a — вероятность некоторого события, то вероятность ненаступления этого события составляет 1−a;
если a и b — вероятности некоторых двух событий, то вероятность совместного наступления этих двух событий не превышает min(a, b);
если a и b — вероятности некоторых двух событий, то вероятность наступления хотя бы одного из этих двух событий больше или равна max(a, b).

История

Devtac ronin

Леонардо Пизанский (Фибоначчи)

1203 г., Фибоначчи (Леонардо Пизанский) (Пиза, Италия) сформулировал «задачи о гирях» («задача Баше-Менделеева») и доказал, что, при разрешении класть гири только на одну чашу весов, наиболее экономичной является двоичная система счисления, а при разрешении класть гири на обе чаши весов, наиболее экономичной является троичная симметричная система счисления, и опубликовал её в «Книге абака» (Liber abaci).

г., (Большой Торрингтон (англ.)русск., графство Девон, Англия, Великобритания) построил механическую троичную вычислительную машину ( с 55-тритным регистром результата), одну из самых ранних механических вычислительных машин.
г., в работе, выполненной под руководством Джона фон Неймана (США), упоминается, но не обсуждается троичная система счисления.

1958 г., Н. П. Брусенцов построил в МГУ первую опытную электронную троичную ЭВМ (компьютер) «Сетунь» на ячейках из ферритдиодных магнитных усилителей переменного тока, работавших в двухбитном троичном коде, четвёртое состояние двух битов не использовалось. Для передачи данных использовалась однопроводная система. В США в то время тоже рассматривали преимущества и недостатки троичного компьютера и после проведённых теоретических исследований строить троичный компьютер не стали.

1959 г., под руководством Н. П. Брусенцова (ВЦ МГУ) разработана первая серийная троичная ЭВМ «Сетунь». С 1962 г. по 1964 г. Казанским заводом математических машин было произведено 46 ЭВМ «Сетунь».

г., Н. П. Брусенцов построил в МГУ вторую электронную троичную ЭВМ (компьютер) «Сетунь-70», ведущим системным программистом которой был Рамиль Альварес Хосе.
г., G. Frieder, A. Fong и C. Y. Chao (SUNY, Буффало, США), создали Ternac — экспериментальный троичный эмулятор с арифметикой над 24-тритными целыми и 48-тритными действительными числами на двоичном компьютере Burroughs B1700.

Трёхуровневая 3-тритная цифровая компьютерная система TCA2

2008 г., (14 марта — 24 мая), Джефф Коннелли (англ. Jeff Connelly), Кираг Патель (англ. Chirag Patel) и Антонио Чавез (англ. Antonio Chavez) при поддержке профессора Филлипа Нико (англ. Phillip Nico) (California Polytechnic State University of San Luis Obispo, San Luis Obispo, Калифорния, США) построили трёхтритную цифровую компьютерную систему TCA2, версия v2.0, в трёхуровневой (3-Level CodedTernary, 3L CT, «однопроводной») системе троичных логических элементов на 1484-х интегральных транзисторах.

Литература

D. C. Rine (ed.), Computer Science and Multiple-Valued Logic. Theory and Applications. Elsevier, 1977, 548p. ISBN 9780720404067
Васильев Н. И. Воображаемая логика. — М.: Наука, 1989.
Карпенко А. С. Многозначные логики // Логика и компьютер. Вып. №4. — М.: Наука, 1997.
Кэррол Льюис. Символическая логика // Льюис Кэррол. История с узелками. — М.: Мир, 1973.
Лукасевич Я. Аристотелевская силлогистика с точки зрения современной формальной логики. — М.: Иностранная литература, 1959.
Слинин Я. А. Современная модальная логика. — Л.: Издательство Ленинградского университета, 1976.
Стяжкин Н. И. Формирование математической логики. — М.: Наука, 1967.
Гетманова А. Д. Учебник по логике. — М.: Владос, 1995. — С. 259—268. — 303 с. — ISBN 5-87065-009-7.
Толковый словарь по вычислительным системам / Под ред. В. Иллингуорта и др.. — М.: Машиностроение, 1990. — 560 с. — ISBN 5-217-00617-X.
Яблонский С.И. Функциональные построения в k-значной логике, Труды Математического института им. В.А.Стеклова, 51, 1958
Янов Ю.И., Мучник А.А., О существовании k-значных замкнутых классов, не имеющих конечного базиса, ДАН СССР, 127, №1, 1959
Гниденко В.М., Нахождение порядков предполных классов в трёхзначной логике, сб. Проблемы кибернетики, вып 8, М., 1962
Post E.L. Two-valued iterative systems, Аnn Math. Studies, 5, №1, 1941
Гектор Гарсиа-Молина, Джеффри Д. Ульман, Дженнифер Уидом «Системы баз данных. Полный курс»

Предыстория

Из истории известно, что первые попытки создать троичную машину начались немного раньше двоичных машин. Английский изобретатель Томас Фоулер (Thomas Fowler), еще 1840 году, построил механическую вычислительную машину. Многие компоненты, счетной троичной машины были сделаны из дерева. Чтобы добиться высокой точности, Фоулеру приходилось создавать ее в более крупных размерах. Длиной в 2 метра, глубиной 1 метр, шириной 30 см. К сожалению, троичная машина Фоулера не сохранилась до наших дней. И многие достижения Томаса Фоулера остались бы неизвестными, если бы не сын, который написал его биографию. В начале 60-х годов МГУ им М.В. Ломоносова была разработана троичная ЭВМ под руководством Н.П. Брусенцова. Новому троичному компьютеру было дано название Сетунь. Машину назвали по имени речки, протекавшей недалеко от университета. Данная машина по своей элементной базе относится ко второму поколению компьютеров. Но по своей архитектуре абсолютно отличается от своих современников, т.к. основывается на троичной логике. Серийный выпуск «Сетуни» был непродолжительным, с 1962 по 1965 год. Но это была первая троичная ЭВМ, выпускаемая серийно. Ее конструктивные особенности были таковы, что она могла адресовать одновременно только один трайт оперативной памяти. Использовалась троичная система счисления: 0, 1, -1. И только для чисел с фиксированной точкой. Оперативная память на ферритовых сердечниках емкостью в 162 трайта. В качестве внешней памяти, использовался магнитный барабан, предшественник современных жестких дисков. На нем вмещалось до 4000 трайт. Пропускная способность шины памяти составляла 54 трайта. Что давало высокую производительность и не слишком частое обращение, к медленной внешней памяти. Троичная машина выполняла порядка четырех тысяч операций в секунду. Ввод и вывод происходил через телетайп и перфоленту. Чтение с последней 800 строк/с, запись 20 строк/секунду. «Сетунь» имел 37 электронных ламп, 300 транзиторов, 4500 полупроводниковых диодов, 7000 ферритовых колец. «Сетунь» занимала около 30 квадратных метра и потребляла 2,5 кВт. Кроме Бруснецова в разработке данной машины участвовали: С.П. Маслов, Е.А. Жоголев, В.В. Веригин. (Для сравнения современный компьютер потребляет 0,3кВт электроэнергии)

Логики

Логики Клини и Приста

Ниже показаны таблицы истинности для логических операций «Сильной логики неопределённости» (strong logic of indeterminacy) Стивена Клини и «Парадоксальной логики» (logic of paradox, LP) Приста. Обе логики имеют три логических значения — «ложь», «неопределённость» и «истина», которые в логике Клини обозначаются буквами F (false), U (unknown), T (true), а в логике Приста числами -1, 0 и 1.

F: false, U: unknown, T: true

NOT(A)
A	¬ A
F	T
U	U
T	F

AND(A, B)
A ∧ B	B
F	U	T
A	F	F	F	F
U	F	U	U
T	F	U	T

OR(A, B)
A ∨ B	B
F	U	T
A	F	F	U	T
U	U	U	T
T	T	T	T

−1: false, 0: unknown, +1: true

NEG(A)
A	¬ A
−1	+1
+1	−1

MIN(A, B)
A ∧ B	B
−1	+1
A	−1	−1	−1	−1
−1
+1	−1	+1

MAX(A, B)
A ∨ B	B
−1	+1
A	−1	−1	+1
+1
+1	+1	+1	+1

Значение U присваивается выражениям, которые реально имеют значение T или F, но в данный момент это значение по каким-то причинам неизвестно, в результате чего возникает неопределённость. Тем не менее, результат логической операции с величиной U может оказаться определённым. Например, поскольку T & F = F и F & F = F, то и U & F = F. В более общем виде: если для некоторой логической операции oper выполняется соотношение oper(F,F)=oper(F,T), то oper(F,U)=oper(F,F)=oper(F,T);аналогично, еслиoper(T,F)=oper(T,T), то oper(T,U)=oper(T,F)=oper(T,T).

При численном обозначении логических значений (–1, 0, 1) логические операции эквивалентны следующим численным операциям:

X¯=−X;{\displaystyle {\bar {X}}=-X;}

X∨Y=max(X,Y);{\displaystyle X\lor Y=max(X,Y);}

X∧Y=min(X,Y).{\displaystyle X\land Y=min(X,Y).}

Операция импликации в логиках Клини и Приста определяется формулой, аналогичной формуле двоичной логики:

X→Y =defX¯∨Y{\displaystyle X\rightarrow Y\ {\overset {\underset {\mathrm {def} }{}}{=}}{\bar {X}}\lor Y}.

Таблицы истинности для неё

IMP_K(A, B), OR(¬A, B)
A → B	B
T	U	F
A	T	T	U	F
U	T	U	U
F	T	T	T

IMP_K(A, B), MAX(−A, B)
A → B	B
+1	−1
A	+1	+1	−1
+1
−1	+1	+1	+1

Это определение отличается от определения импликации, принятого в логике Лукасевича.

Будущее

Дональд Кнут отмечал, что из-за массового производства двоичных компонентов для компьютеров, троичные компьютеры занимают очень малое место в истории вычислительной техники. Однако троичная логика элегантнее и эффективнее двоичной и в будущем, возможно, вновь вернутся к её разработке.

В работе возможным путём считают комбинацию оптического компьютера с троичной логической системой.
По мнению авторов работы, троичный компьютер, использующий волоконную оптику, должен использовать три величины: 0 или ВЫКЛЮЧЕНО, 1 или НИЗКИЙ, 2 или ВЫСОКИЙ, т.е. трёхуровневую систему. В работе же автор пишет, что более быстродействующей и более перспективной является трёхчастотная система с тремя величинами: (f1,f2,f3) равными «001» = «0», «010» = «1» и «100» = «2», где 0 — частота выключена, а 1 — частота включена.

Будущий потенциал троичной вычислительной техники был также отмечен такой компанией как Hypres, которая активно участвует в её изучении. IBM в своих публикациях также сообщает о троичной вычислительной технике, но активно в этом направлении не участвует.

Элементы троичных ЭВМ (компьютеров)[править | править код]

Известны троичные элементы следующих видов:

Импульсныеправить | править код

Ферритодиодные троичные элементы Н. П. Брусенцова, аналогичные двоичным элементам ЛЭМ-1 Л. И.Гутенмахера (магнитные усилители)

Трёхуровневыеправить | править код

В трёхуровневых потенциальных линиях передачи цифровых данных (3-Level CodedTernary, 3L CT, «однопроводных») трём устойчивым состояниям соответствуют три уровня напряжения (положительное, нулевое, отрицательное), (высокое, среднее, низкое). Имеют меньшее итоговое быстродействие, чем обычная двоичная система .

Амплитуда наибольшего сигнала помехи равной помехоустойчивости с двухуровневыми элементами не более (+/-)Uп/6 (16,7% от Uп), при делении всего диапазона напряжений на три равные части и номинальных напряжениях сигналов в срединах поддиапазонов.

Недостатки: 1. необходимость, для равной помехоустойчивости с обычной двоичной системой, увеличения размаха сигнала в 2 раза, 2. неодинаковость среднего состояния с верхним и нижним состояниями, 3. неодинаковость амплитуд переходов из крайних состояний в среднее (одинарная амплитуда) и переходов из одного крайнего состояния в другое крайнее состояние (двойная амплитуда).

Двухуровневыеправить | править код

Амплитуда наибольшего сигнала помехи не более (+/-)Uп/4 (25% от Uп), при делении всего диапазона напряжений на две равные части и номинальных напряжениях сигналов в срединах поддиапазонов.

Двухуровневые, потенциальные (2-Level BinaryCodedTernary, 2L BCT), в которых логические элементы (инверторы) имеют два устойчивых состояния с двумя уровнями напряжения (высокое, низкое), а троичность работы достигается системой обратных связей (троичный триггер). Амплитуда сигнала помехи до Uп/2 (до 50 % от Uп).

Двухбитные

Двухуровневые двухбитные (2-Level 2-Bit BinaryCodedTernary, 2L 2B BCT, «двухпроводные»). По скорости равны троичным двухуровневым трёхбитным триггерам. По сравнению с обычными двоичными триггерами в 1,5 раза увеличивают прямые аппаратные затраты.

Недостатки:

1. два провода на один разряд.

Трёхбитные

Двухуровневые трёхбитные (2-Level 3-Bit BinaryCodedTernary, 2L 3B BCT, «трёхпроводные»). По скорости равны троичным двухуровневым двухбитным триггерам. По сравнению с обычными двоичными RS-триггерами увеличивают объём хранимых и передаваемых данных в 1,5 раза на один разряд, но и аппаратные затраты тоже увеличиваются. Быстродействие выше, чем в обычной двоичной системе, но ниже, чем в четверичной четырёхбитной системе, но аппаратные затраты растут меньше, чем в четверичной четырёхбитной системе. Из-за избыточности трёхбитного кода появляется возможность обнаружения одиночных однобитных ошибок на аппаратном уровне, что может оказаться полезным в устройствах повышенной надёжности и может найти применение в устройствах, в которых надёжность и быстродействие являются более значимыми параметрами, чем аппаратные затраты.

Недостатки:

1. три провода на один разряд.

Смешанныеправить | править код

Смешанные, в которых вход данных трёхуровневый по одной линии и земле, а выход данных двухуровневый по трём линиям и земле.

Будущее

В работе возможным путём считают комбинацию оптического компьютера с троичной логической системой.
По мнению авторов работы, троичный компьютер, использующий волоконную оптику, должен использовать три величины: 0 или ВЫКЛЮЧЕНО, 1 или НИЗКИЙ, 2 или ВЫСОКИЙ, то есть трёхуровневую систему. В работе же автор пишет, что более быстродействующей и более перспективной является трёхчастотная система с тремя величинами: (f1,f2,f3) равными «001» = «0», «010» = «1» и «100» = «2», где 0 — частота выключена, а 1 — частота включена.

Трёхзначные логики

Трёхзначная логика была исторически первой многозначной логикой и является простейшим расширением двузначной логики. Перечень истинностных значений трёхзначной логики помимо «истинно» и «ложно» включает также третье значение, которое, как правило, трактуется как «неопределено», «неизвестно» или «ошибочно». В последнем случае логику обычно называют частичной.

В трёхзначной логике, естественно, не соблюдается закон исключённого третьего. Вместе с тем, важным свойством трёхзначных логик, отражающим их адекватность, является то, что все они представляют собой расширения классической двузначной логики. То есть, в предположении, что интерпретируемые символы не принимают третьего истинностного значения, семантика формул в трёхзначной логике такая же, как и в двузначной.

Логики[править | править код]

Логики Клини и Пристаправить | править код

F: false, U: unknown, T: true

NOT(A)
A	¬ A
F	T
U	U
T	F

AND(A, B)
A ∧ B	B
F	U	T
A	F	F	F	F
U	F	U	U
T	F	U	T

OR(A, B)
A ∨ B	B
F	U	T
A	F	F	U	T
U	U	U	T
T	T	T	T

−1: false, 0: unknown, +1: true

NEG(A)
A	¬ A
−1	+1
+1	−1

MIN(A, B)
A ∧ B	B
−1	+1
A	−1	−1	−1	−1
−1
+1	−1	+1

MAX(A, B)
A ∨ B	B
−1	+1
A	−1	−1	+1
+1
+1	+1	+1	+1

X¯=−X;{\displaystyle {\bar {X}}=-X;}

X∨Y=max(X,Y);{\displaystyle X\lor Y=max(X,Y);}

X∧Y=min(X,Y).{\displaystyle X\land Y=min(X,Y).}

Операция импликации в логиках Клини и Приста определяется формулой, аналогичной формуле двоичной логики:

X→Y =defX¯∨Y{\displaystyle X\rightarrow Y\ {\overset {\underset {\mathrm {def} }{}}{=}}{\bar {X}}\lor Y}.

Таблицы истинности для неё

IMP_K(A, B), OR(¬A, B)
A → B	B
T	U	F
A	T	T	U	F
U	T	U	U
F	T	T	T

IMP_K(A, B), MAX(−A, B)
A → B	B
+1	−1
A	+1	+1	−1
+1
−1	+1	+1	+1

Это определение отличается от определения импликации, принятого в логике Лукасевича.

Функциональный подход

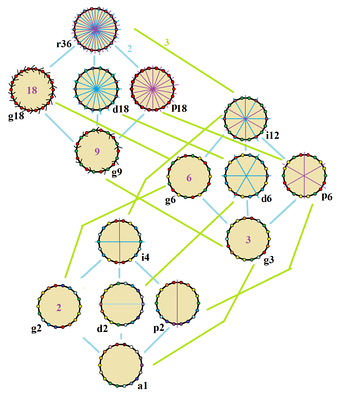
Назовём функцию y=f(x1,x2,…,xn){\displaystyle y=f(x_{1},\;x_{2},\;\ldots ,\;x_{n})} функцией трёхзначной логики, если все её переменные принимают значения из множества {0,1,2} и сама функция принимает значения из этого же множества. Примеры функций: max(x,y), min(x,y), x+1 (mod 3). Обозначим P3{\displaystyle P_{3}} множество всех функций трёхзначной логики. Под операцией над функциями будем понимать суперпозицию. Класс функций K из P3{\displaystyle P_{3}} назовём замкнутым, если любая суперпозиция функций из K принадлежит K. Система функций класса K называется полной, если любая функция из K может быть представлена суперпозицией функций этой системы. Полная система называется базисом, если никакая функция из этой системы не может быть представлена суперпозицией остальных функций этой системы. Доказано, что в P3{\displaystyle P_{3}} существует конечный базис (в частности, состоящий из одной функции). Замкнутый класс K называется предполным, если он не совпадает с P3{\displaystyle P_{3}}, но добавление любой функции, ему не принадлежащей, порождает P3{\displaystyle P_{3}}. С.В. Яблонским доказано, что в P3{\displaystyle P_{3}} существует 18 предполных классов. Также доказано, что все они имеют конечные базисы, в частности, состоящие из функций, зависящих не более чем от двух переменных. Ю.И.Янов и А.А.Мучник доказали, что в P3{\displaystyle P_{3}} существуют классы функций, не имеющие базиса, и классы функций, имеющие бесконечный базис. Отсюда следует, что множество замкнутых классов в P3{\displaystyle P_{3}} имеет мощность континуума. Этим трёхзначная (и любая многозначная) логика существенно отличается от двухзначной, где, как доказано Постом, все замкнутые классы имеют конечный базис и множество замкнутых классов счётно.

Заключение

Анализируя данный реферат, задаешься вопросом: Раз уж у Троичных ЭВМ (Или Трайтов, как уже привыкли) так много преимуществ, почему растет и процветает двоичная арифметика в современных ЭВМ. Казалось бы и затрат на построение меньше, и алгебра логика уже была полностью продумана, и даже были созданы первые успешные образцы Трайтов. Безусловно у Трайтов есть и недостатки, о которых я писал выше, но даже, учитывая их, Трайты перспективнее ЭВМ с двоичной логикой. Проблема в том, что к моменту освоения троичной алгебры и построения моделей таких ЭВМ, двоичные компьютеры захватывали все большую и большую часть рынка. Было написано много программ, область применения которых распространялось по всему миру. В наши дни Трайты уже совсем вымерли и образцы вы можете встретить только в музеях ЭВМ. В перспективах возрождения Троичных ЭВМ: Возможно в узких кругах, компаниях будут возобновлены разработки Трайтов со своими системами и программами для выполнения конкретных задач.