Инерция и момент инерции: базовые сведения

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Hа рисунке приведены графики зависимости пути и скорости тела от времени. Какой график соответствует равноускоренному движению?

2. Автомобиль, начав двигаться из состояния покоя но прямолинейной дороге, за 10 с приобрел скорость 20 м/с. Чему равно ускорение автомобиля?

1) 200 м/с2 2) 20 м/с2 3) 2 м/с2 4) 0,5 м/с2

3. На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси ​\( Оx \)​. У какого из тел в момент времени ​\( t_1 \)​ скорость движения равна нулю?

4. На рисунке представлен график зависимости проекции ускорения от времени для тела, движущегося прямолинейно вдоль оси ​\( Оx \)​.

Равноускоренному движению соответствует участок

1) только ОА 2) только АВ 3) только ОА и ВС 4) только CD

5. При изучении равноускоренного движения измеряли путь, пройденный телом из состояния покоя за последовательные равные промежутки времени (за первую секунду, за вторую секунду и т.д.). Полученные данные приведены в таблице.

Чему равен путь, пройденный телом за третью секунду?

1) 4 м 2) 4,5 м 3) 5 м 4) 9 м

6. На рисунке представлены графики зависимости скорости движения от времени для четырёх тел. Тела движутся по прямой.

Для какого(-их) из тел — 1, 2, 3 или 4 — вектор ускорения направлен противоположно вектору скорости?

1) только 1 2) только 2 3) только 4 4) 3 и 4

7. Используя график зависимости скорости движения тела от времени, определите его ускорение.

1) 1 м/с2 2) -1 м/с2 3) 2 м/с2 4) -2 м/с2

8. При изучении равноускоренного движения измеряли скорость тела в определённые моменты времени. Полученные данные, приведены в таблице. Чему равна скорость тела в момент времени 3 с?

1) 0 м/с 2) 2 м/с 3) 4 м/с 4) 14 м/с

9. На рисунке приведены графики зависимости скорости движения четырёх тел от времени. Ускорение какого из тел равно -1,5 м/с?

1) 1 2) 2 3) 3 4) 4

10. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 30-й секунды. Считать, что характер движения тела не изменился.

1) 14 м/с 2) 20 м/с 3) 62 м/с 4) 69,5 м/с

11. Два тела движутся по оси ​\( Оx \)​. На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) В промежутке времени ​\( t_3-t_5 \)​ тело 2 движется равноускоренно. 2) К моменту времени ​\( t_2 \)​ от начала движения тела прошли одинаковые пути. 3) В промежутке времени ​\( 0-t_3 \)​ тело 2 находится в покое. 4) В момент времени ​\( t_5 \)​ тело 1 останавливается. 5) В промежутке времени ​\( t_3-t_4 \)​ ускорение ​\( a_x \)​ тела 1 отрицательно.

12. На рисунке представлен график зависимости проекции скорости от времени для тела, движущегося вдоль оси Ох.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) Участок ОА соответствует ускоренному движению тела. 2) Участок АВ соответствует состоянию покоя тела. 3) В момент времени ​\( t_1 \)​ тело имело максимальное по модулю ускорение. 4) Момент времени ​\( t_3 \)​ соответствует остановке тела. 5) В момент времени ​\( t_2 \)​ тело имело максимальное по модулю ускорение.

Часть 2

13. Зависимость координаты от времени для некоторого тела описывается уравнением ​\( x=12t-t^2 \)​. В какой момент времени скорость движения равна нулю?

Момент инерции

Инерция проявляется не только для прямолинейного движения, но и при вращении тел. В двигателе есть специальное устройство – маховик (на рисунке справа маховик покрашен темно-серым цветом и имеет зубчики). Инерция его вращения помогает работать двигателю нормально. Энергия расширяющихся газов при воспламенении топлива толкает поршень вниз, а затем ему нужно идти вверх, выталкивая продукты сгорания. Без маховика поршень не смог бы провернуть коленвал без рывков. Двигатель без маховика заглохнет.

Ну а со спинерами и волчками знакомы многие.

Вот только в приведенных примерах форма тела не меняется. А изменится ли инертность тела при изменении его формы?

Вращение на фигурном катании

Многие могут вспомнить фигурное катание. Масса тела фигуриста за выступление не меняется. Но его скорость вращения мгновенно увеличивается, стоит прижать руки и ноги, и вытянуться в струнку. Т.е. при уменьшении радиуса тела скорость вращения увеличивается. Т.е. инертность тела должна уменьшиться? Давайте разбираться.

Вернемся к формулам. Скорость вращающегося тела описывается как произведение угловой скорости (омега) на радиус:

Скорость вращающегося тела

При этом кинетическая энергия вращающегося тела примет вид:

Синим цветом выделено произведение массы тела на радиус в квадрате. Эта величина называется моментом инерции вращающегося тела и обозначается латинской буквой I (и).

Мерой инертности вращающего тела выступает момент инерции, который зависит от массы тела и расстояния этой массы от центра вращения.

Представим, что девочка не только вращает груз над собой, но и идет. Тогда полная кинетическая энергия девочки с грузом примет вид:

Первая часть описывает кинетическую энергию двигающейся прямолинейно с некоторой скоростью девочки с грузом, а вторая – кинетическую энергию вращающегося груза. Полная кинетическая энергия — это сумма энергии прямолинейно движущегося тела и энергии вращающегося тела. Точно так же кинетическая энергия будет рассчитываться для движущегося по столу раскрученного волчка или съезжающего с наклонной плоскости цилиндра.

Так как вращающееся тело может иметь форму, отличную от точки или маленького шарика, то и формула момента инерции для более точных расчетов может принимать разный вид.

Некоторые формулы для расчета момента инерции для тел разной формы

Пример.

Цилиндры одинаковой массы (m1 = m2), но разного радиуса (r₁ < r₂), скатываются с горки высотой h. Какой цилиндр скатится быстрее? Какое из тел обладает меньшей инертностью?

Цилиндры одинаковой массы, но разного радиуса, скатываются с горки высотой h

В верхней точке кинетическая энергия обоих цилиндров будет равна нулю, так как скорость равна нулю. Потенциальная энергия будет одинаковой и максимальной.

Потенциальная и кинетическая энергия 1 и 2 цилиндра верхней точке

При скатывании цилиндров по закону сохранения энергии потенциальная энергия переходит в кинетическую и в самой нижней точке будет равна нулю, так как высота равна нулю. А кинетическая энергия в нижней точке будет складываться из поступательной кинетической энергии и кинетической энергии вращающегося тела и у обоих тел также будет одинаковой, так как их потенциальные энергии были равны.

Кинетическая энергия первого и второго цилиндра в нижней точке

Но так как радиус первого тела меньше второго, то и момент инерции первого тела меньше второго и будет справедливо:

Тогда для кинетической энергии поступательного движения будет справедливо отношение:

Следовательно, скорость первого цилиндра должна быть выше скорости второго, и он скатится быстрее. Так как мерой инертности вращающегося тела является момент инерции, то первое тело с меньшим радиусом и меньшим моментом инерции будет обладать меньшей инертностью, чем второе. Разогнаться под действием каких-либо сил (силы тяжести) такому телу проще.

§ 14. Инерциальные и неинерциальные системы отсчета. Силы инерции

Система отсчета, движущаяся (относительно звезд) равномерно и прямолинейно (т. е. по инерции), называется инерциальной. Очевидно, что таких систем отсчета — неисчислимое множество, поскольку любая система, движущаяся относительно некоторой инерциальной системы отсчета равномерно и прямолинейно, тоже инерциальна, Системы отсчета, движущиеся (относительно инерциальной системы) с ускорением, называются неинерциальными.

Опыт показывает, что

во всех инерциальных системах отсчета все механические процессы протекают совершенно одинаково (при одинаковых условиях).

Это положение, названное механическим принципом относительности (или принципом относительности Галилея), было сформулировано в 1636 г. Галилеем. Галилей пояснял его на примере механических процессов, совершающихся в каюте корабля, плывущего равномерно и прямолинейно по спокойному морю. Для наблюдателя, находящегося в каюте колебание маятника, падение тел и другие механические процессы протекают точно так же, как и на неподвижном корабле. Поэтому, наблюдая эти процессы, невозможно установить ни величину скорости, ни даже сам факт движения корабля. Чтобы судить о движении корабля относительно какой-либо системы отсчета (например, поверхности еоды), необходимо вести наблюдения и за этой системой (видеть, как удаляются предметы, лежащие на воде, и т. п.).

К началу XX в. выяснилось, что не только механические, но и тепловые, электрические, оптические и все другие процессы и явления природы протекают совершенно одинаково во всех инерциальных системах отсчета. На этом основании Эйнштейн в 1905 г. сформулировал обобщенный принцип относительности, названный впоследствии принципом относительности Эйнштейна:

во всех инерциальных системах отсчета все физические процессы протекают совершенно одинаково (при одинаковых условиях).

Этот принцип наряду с положением о независимости скорости распространения света в вакууме от движения источника света (см. § 20) лег в основу специальной теории относительности, разработанной Эйнштейном.

Законы Ньютона и другие рассмотренные нами законы динамики, выполняются только в инерциальных системах отсчета. В неинерциальных системах отсчета эти законы, вообще говоря, уже несправедливы. Рассмотрим простой пример, поясняющий последнее утверждение.

На совершенно гладкой платформе, движущейся равномерно и прямолинейно, лежит шар массой на этой же платформе находится наблюдатель. Другой наблюдатель стоит на Земле недалеко от места, мимо которого вскоре должна пройти платформа. Очевидно, что оба наблюдателя связаны с инерциальными системами отсчета.

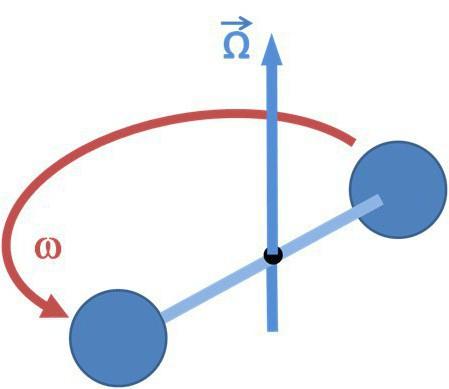
Экспериментальная проверка и наблюдения эффекта в астрофизике

Эффект Лензе-Тирринга наблюдается как прецессия плоскости орбиты пробной массы, обращающейся вокруг массивного вращающегося тела, либо как прецессия оси вращения гироскопа в окрестностях такого тела.

Впервые в мире был измерен Иньяцио Чьюфолини (итал. Ignazio Ciufolini) из итальянского университета Лечче и Эррикосом Павлисом (Erricos Pavlis) из Мерилендского университета, Балтимор, США. Их результаты были опубликованы в октябре 2004 года. Чьюфолини и Павлис провели компьютерный анализ нескольких миллионов измерений дальности, полученных методом лазерной дальнометрии по уголковым отражателям на спутниках LAGEOS и LAGEOS II (LAser GEOdynamics Satellite), запущенных для изучения геодинамики и уточнения параметров гравитационного поля Земли. Обнаруженный средний поворот орбит спутников, вызванный эффектом Лензе — Тирринга, составляет 47,9 угловой микросекунды в год (mas/год), или 99 % от значения, предсказанного теорией Эйнштейна (48,2 mas/год), с оцененной погрешностью ±10 %. По мнению некоторых исследователей, реальная точность может быть порядка 20-30 %. G. Renzetti опубликовал в 2013 году обзорную статью, посвященную попытке измерить эффект Лензе-Тирринга с использованием искусственных спутников Земли.

Для экспериментального подтверждения эффекта, вместе с другим, более существенным эффектом геодезической прецессии, американское космическое агентство NASA осуществило спутниковую программу Gravity Probe B. Космический аппарат GP-B успешно завершил свою программу в космосе. Первые результаты обнародованы в апреле 2007 года, но в связи с выявившимся лишь на орбите эффектом влияния вмороженного распределения электрических зарядов на гироскопах на их вращение точность обработки данных была недостаточна, чтобы выделить эффект (поворот оси на 0,039 угловой секунды в год в плоскости земного экватора). Учёт мешающих эффектов позволил выделить ожидаемый сигнал, окончательные результаты ожидались в декабре 2007 года, но анализ данных продлился до мая 2011 года. Окончательные итоги миссии были объявлены на пресс-конференции по NASA-TV 4 мая 2011 года и опубликованы в Physical Review Letters.

Результат Gravity Probe B оказался менее точным (хотя проектная погрешность должна была составлять порядка 1 %, влияние электрического заряда привело к ухудшению относительной погрешности измерения эффекта Лензе — Тирринга до ~20 %), однако тоже подтвердил предсказания ОТО. Измеренная величина геодезической прецессии составила −6601,8±18,3 mas/год, а эффекта увлечения — −37,2±7,2 mas/год (ср. с предсказываемыми теоретическими значениями 6606,1 mas/год и 39,2 mas/год).

13 февраля 2012 года в 14:00 МСК ЕКА успешно осуществило запуск ракеты Vega c 9 различными спутниками на борту, одним из них был аппарат LARES, основной миссией которого является проверка эффекта Лензе-Тирринга. Существуют различные мнения о реальной точности, достижимой в такой миссии.

Решение задач

Первый пример.

Определите, является ли инерциальной системой отсчета: а) искусственный спутник Земли; б) детский аттракцион.

Ответ. В первом случае не идет речи об инерциальной системе отсчета, поскольку спутник передвигается по орбите под воздействием силы земного притяжения, следовательно, движение происходит с некоторым ускорением.

Аттракцион также нельзя считать инерциальной системой, поскольку его вращательное движение происходит с некоторым ускорением.

Второй пример.

Система отчета прочно связана с лифтом. В каких ситуациях ее можно называть инерциальной? Если лифт: а) падает вниз; б) передвигается равномерно вверх; в) ускоренно поднимается; г) равномерно направляется вниз.

Ответ. а) При свободном падении появляется ускорение, поэтому система отсчета, что связана с лифтом, не будет являться инерциальной.

б) При равномерном передвижении лифта система является инерциальной.

в) При движении с некоторым ускорением систему отсчета считают инерциальной.

г) Лифт передвигается замедленно, имеет отрицательное ускорение, поэтому нельзя назвать систему отсчета инерциальной.

Относительность Галилея

Все инерциальные системы отсчета имеют важное свойство, которое описывается принципом относительности. Суть его заключается в том, что любое механическое явление при одинаковых начальных условиях осуществляется одинаково независимо от выбираемой системы отсчета

Равноправие ИСО по принципу относительности выражается в следующих положениях:

• В таких системах законы механики одинаковы, поэтому любое уравнение, которое описывается ними, выражается через координаты и время, остается неизменным.
• Результаты проводимых механических опытов позволяют устанавливать, будет ли система отсчета покоиться, или она совершает прямолинейное равномерное движение. Любая система условно может быть признана неподвижной, если другая при этом совершает относительно нее движение с некоторой скоростью.
• Уравнения механики остаются неизменными по отношению к преобразованиям координат в случае перехода от одной системы ко второй. Можно описать одно и то же явление в различных системах, но их физическая природа при этом меняться не будет.

Свойства инерциальных систем отсчёта

Всякая система отсчёта, движущаяся относительно ИСО равномерно, прямолинейно и без вращения, также является ИСО. Согласно принципу относительности, все ИСО равноправны, и все законы физики инвариантны относительно перехода из одной ИСО в другую. Это значит, что проявления законов физики в них выглядят одинаково, и записи этих законов имеют одинаковую форму в разных ИСО.

Предположение о существовании хотя бы одной ИСО в изотропном пространстве приводит к выводу о существовании бесконечного множества таких систем, движущихся друг относительно друга равномерно, прямолинейно и поступательно со всевозможными скоростями. Если ИСО существуют, то пространство будет однородным и изотропным, а время — однородным; согласно теореме Нётер, однородность пространства относительно сдвигов даст закон сохранения импульса, изотропность приведёт к сохранению момента импульса, а однородность времени — к сохранению энергии движущегося тела.

Если скорости относительного движения ИСО, реализуемых действительными телами, могут принимать любые значения, связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Галилея.

В специальной теории относительности скорости относительного движения
ИСО, реализуемых действительными телами, не могут превышать некоторой конечной скорости «c» (скорость распространения света в вакууме) и связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Лоренца.

Приложения

1. ↑ Тарг С. М. // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 494—495. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
2. Сила инерции — статья из Большой советской энциклопедии. 
3.  Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 14—15. — 320 с.
4. ↑ Савельев И. В. Курс общей физики. Том 1. Механика. Молекулярная физика. — М., Наука, 1987. — Тираж 233000 экз. — с. 119—120
5. ↑ Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М., Наука, 1975. — Тираж 350000 экз. — с. 291—292
6. Кошкин Н. И., Ширкевич М. Г. Справочник по элементарной физике.- М., Наука, 1988. — Тираж 300000 экз. — с. 33
7.  Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 14—18. — 320 с.
8. ↑
9. Walter Greiner Klassische Mechanik II. Wissenschaftlicher Verlag Harri Deutsch GmbH. Frankfurt am Main. 2008 ISBN 978-3-8171-1828-1
10.  Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 82. — 368 с. — ISBN 5-93972-051-X.
11. Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
12. ↑ Фейнман Р., Лейтон Р., Сэндс М. Выпуск 1. Современная наука о природе. Законы механики // Фейнмановские лекции по физике. — М.: «Мир», 1965. — С. 225.
13. Седов Л. И. Об основных моделях механики. М.: МГУ, 1992. Стр 17.; Седов Л. И. Очерки, связанные с основами механики и физики. М.: Знание, 1983. Стр 19.
14. Матвеев А. Н. Механика и теория относительности. М.: Высшая школа, 1979. Стр 393. (в 3-е изд. 2003. Стр.393)
15. А. Ишлинский при переиздании своей работы удалил эти термины («Классическая механика и силы инерции», 1987, с. 279): … термин «реальная сила» и «фиктивная сила» понимались по-разному. Считаю, что лучше не спорить на эту тему и от упомянутых слов вообще отказаться.
16. «„Силы инерции“ — не силы».
    Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 21. — 46 с.
17. Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 182. — 416 с. — ISBN 5-06-003117-9.
18. ↑ Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 19. — 46 с.
19. Тарг С. М. // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 494. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
20.  Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 16. — 368 с. — ISBN 5-93972-051-X.
21. Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2005. — Т. I. Механика. — С. 84. — 560 с. — ISBN 5-9221-0225-7.
22. ↑
23. Встречается утверждение, что применительно к силе Лоренца сказанное не верно и требует дополнительного уточнения (Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132). Согласно другой точке зрения, «в электродинамике силы противодействия силам Лоренца приложены к электромагнитному полю (подстрочное примечание: Стоит отметить, что ещё недавно некоторые видные учёные считали, что сила Лоренца вообще не удовлетворяет закону действия и противодействия…) как к физическому объекту, претерпевающему соответствующее влияние» (Седов, Очерки, с. 17).
24.  Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 8. — 320 с.
25. ↑ Хайкин, Семён Эммануилович. Силы инерции и невесомость. — 1. — М., «Наука». Главная редакция физико-математической литературы. 1967 г..— С. 129—130, 188—189. — 312 с.
26. . snob.ru. Дата обращения 24 января 2020.
27. Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 362. — 560 с. — ISBN 5-9221-0225-7.
28. ↑
29. , с. 165—166.
30. , с. 165.
31. Китайгородский А. И. Введение в физику. М:Изд.-во «Наука», гл.ред.физико-математической литературы.1973
32. Тарг С. М. // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 496. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
33. Грушинский Н. П. Основы гравиметрии. — М.: «Наука», 1983. — С. 34. — 351 с.
34. Krigel A. M. The theory of the index cycle in the general circulation of the atmosphere // Geophys. Astrophys. Fluid Dynamics.— 1980.— 16.— p. 1-18.

Общие сведения

Инерциальная навигационная система (система инерциальной навигации, навигационное устройство), в основу работы которой положены классические (ньютоновские) законы механики. В ИНС исходной (главной) системой отсчёта, по отношению к которой производятся инерциальные измерения, служит инерциальная (абсолютная, т. е. неподвижная относительно звёзд) система. Посредством ИНС определяют координаты, скорость, ускорение и др. основные параметры движения объекта (самолёта, ракеты, космического корабля, надводных и подводных судов и др.). ИНС имеют перед другими навигационными системами большие и важные преимущества — универсальность применения, возможность определения основных параметров движения, автономность действия, абсолютную помехозащищенность. Эти качества определили ИНС как наиболее перспективную навигационную систему.

Принцип действия

Принцип действия ИНС состоит в моделировании поступательного движения объекта, характеризуемого изменением во времени ускорения,
скорости и координат, подобным процессом движения воспринимающего элемента (массы) пространственного (трёхкомпонентного) акселерометра (в общем случае с компенсацией гравитационного ускорения).

Исходной информацией для инерциальной навигационной системы является ускорение судна, на котором она установлена. Двойное интегрирование вектора ускорения дает необходимую информацию для вычисления скорости и координат. ИНС не связана с внешними источниками информации (курс, скорость). Ориентирование измерительных осей акселерометров по заданным направлениям производится свободными или управляемыми (по сигналам от акселерометров) гироскопическими устройствами (гироскопом, гиростабилизатором, гирорамой и др.) или астростабилизаторами, а также сочетанием этих средств.

ИНС весьма сложны и дорогостоящи. Срок службы их меньше, чем у обычных гироскопических приборов. Для правильного функционирования перед стартом объекта требуется ввести начальные данные по координатам пункта старта и скорости, произвести ориентирование инерциальных измерителей. Точность некорректируемых инерциальных навигационных систем зависит от времени. Поэтому возможность получения информации от системы, удовлетворяющей заданным требованиям, ограничена во времени. Так, за час полёта лучшие образцы ИНС имеют погрешность в определении координат примерно 1,5—5 км. Для уменьшения погрешностей и расширения возможностей использования применяют различные способы коррекции от радионавигационных, радиолокационных и астронавигационных средств.

XXI век

В последнее десятилетие наиболее распространенным типом ИНС стали бесплатформенные инерциальные навигационные системы (БИНС). Они широко применяются в аэрокосмической технике и начали применяться в морских и наземных системах. Это стало возможным после преодоления ряда сложных технических проблем. В ИНС надводных кораблей и судов обычно используются динамически настраиваемые или поплавковые гироскопы. Они обеспечивают выработку навигационных данных и гироскопическую стабилизацию вооружения и различных технических средств корабля. Курс вырабатывается с точностью порядка единиц угловых минут, координаты – с точностью порядка нескольких десятков метров, углы качки – с точностью не хуже 1 угл. мин. В литературе можно встретить совмещенные измерители ИНС / ГАГК (гиро-азимут-горзонт компас) в основе работы которого лежит инерциальный принцип. Согласно протоколам обмена, мы получаем объединенный вектор навигационных параметров этих систем.

Устройство инерциальной системы

Основа работы ИНС заключается в измерении ускорений летательного аппарата и его угловых скоростей относительно трех осей самолета для того, чтобы исходя из этих данных определить местоположение самолета, его скорость, курс и другие параметры. По результатам анализа объект стабилизируется, и может использоваться автоматическое управление.

Лазерный гироскоп

Для сбора информации о полете в состав ИНС включаются акселерометры, считывающие линейное ускорение, и гироскопы, позволяющие определить углы наклона самолета относительно основных осей: тангаж, рысканье и крен. Точность полученной информации зависит от характеристик этих приборов. Анализом данных занимается компьютер, который затем по определенным навигационным алгоритмам корректирует движение объекта.

ИНС делятся на платформенные и бесплатформенные. Основой для платформенных ИНС служит гиростабилизированная платформа. В бесплатформенных системах акселерометры и гироскопы жестко связаны с корпусом прибора. Функции платформы моделируются математически вычислительной системой. Бесплатформенные системы выгодно отличаются меньшим весом и габаритами, а также возможностью работать при значительных перегрузках.

Преимущества ИНС перед другими навигационными системами заключаются в их полной независимости от внешних источников данных, повышенной защите от помех, высокой информативности и возможности передавать информацию на большой скорости. Отсутствием какого-либо излучения при работе ИНС обеспечивается скрытность объекта, на котором она используется.

Недостатком ИНС можно назвать ошибки, которые накапливаются с течением времени в получаемой от приборов информации. Это могут быть как методические ошибки, так и ошибки, связанные с неверной начальной настройкой оборудования. Для их коррекции создаются интегрированные навигационные системы, где данные, получаемые ИНС, дополняются данными, поступающими от неавтономных систем, например спутниковой навигации. Еще одним относительным минусом ИНС является высокая стоимость входящего в их состав оборудования.
 

Инерция, кинетическая энергия, работа

Приведем другой пример. Представь тяжелоатлета… Даже двух, которые решили поставить мировой рекорд и сдвинуть самолет. Им придется приложить немало сил, чтобы вначале разогнать самолет от нуля до некоторой скорости, а потом поддерживать эту скорость, преодолевая силу трения, направленную назад. Конечно, проще сдвинуть с места (преодолеть инерцию покоя) и разогнать до большой скорости тело меньшей массы, например, футбольный мяч. Инертность самолета во много раз больше инертности футбольного мяча.

Силачи тянут Ил-76

А к какому трюку прибегает фокусник, чтобы в случае со скатертью все предметы остались на столе? Правильно, нужно выдернуть скатерть за наименьшее время. Чем меньше время, тем меньше энергии перейдет с силой трения на предметы и они просто не успеют разогнаться. 

Трюк со скатертью

Энергия движущегося тела называется кинетической энергией и измеряется в Джоулях. Если тело неподвижно, кинетическая энергия равна нулю.

Чтобы разогнать тело массой m до нужной скорости V из состояния покоя (например, самолет), нужно выполнить работу, равную кинетической энергии разогнанного тела (без учета разных потерь):

Работа по изменению кинетической энергии тела совершается за счет приложения к нему некоторой силы – силы тяжести, силы трения, силы воздействия на него другого тела (тяжелоатлета-силача, дующего ветра, реактивной тяги ракетного двигателя и пр.).

Пусть силач разогнал до 0.1 м/с (10 сантиметров в секунду) легковую машину массой 1200 кг и самолет Ил-76 массой 88 500 кг в космосе (не будем учитывать силу трения). Тогда для преодоления инерции этих тел ему пришлось сжечь мышечной энергии на 6 Дж и 442,5 Дж соответсвенно. Т.е. на преодоление инерции покоя у самолета у спортсмена уйдет в 74 раза больше энергии, чем на автомобиль.

Чтобы остановить тело массой m, движущееся со скоростью V, нужно совершить обратную работу, равную отрицательному значению кинетической энергии этого тела:

Т.е. чем больше скорость тела и его масса, тем больше энергии на преодоление инерции движения надо затратить.

Если выключить мотор, машина под действием силы трения ее движущихся частей друг о друга, силы трения о воздух корпуса и силы трения колес об асфальт остановится сама. Но остановить машину можно и быстрее, увеличив силу трения с помощью тормозных дисков, т.е. выжав педаль тормоза.

При равной скорости масса грузовика намного больше, а значит больше его кинетическая энергия. Двигаясь накатом грузовик остановится дальше, чем легковой автомобиль – его инертность выше. Кстати, можно ли остановить грузовик быстрее легкового автомобиля и при каких условиях?

История

Древнегреческие учёные, судя по дошедшим до нас сочинениям, размышляли о причинах совершения и прекращения движения. В «Физике» Аристотеля (IV век до н. э.) приводится такое рассуждение о движении в пустоте:

Никто не сможет сказать, почему , приведенное в движение, где-нибудь остановится, ибо почему оно скорее остановится здесь, а не там? Следовательно, ему необходимо или покоиться, или двигаться до бесконечности.

Однако в другом труде «Механика», приписываемом Аристотелю, утверждается:

Движущееся тело останавливается, если сила, его толкающая, прекращает своё действие.

Наблюдения действительно показывали, что тело останавливалось при прекращении действия толкающей его силы. Естественное противодействие внешних сил (трения, сопротивления воздуха и т. п.) движению толкаемого тела при этом не учитывалось. Поэтому Аристотель связывал неизменность скорости движения любого тела с неизменностью прилагаемой к нему силы.

Только через два тысячелетия Галилео Галилей (1564—1642) смог исправить эту ошибку «аристотелевской физики». В своем труде «Беседы о двух новых науках» Галилей писал:

…скорость, однажды сообщенная движущемуся телу, будет строго сохраняться, поскольку устранены внешние причины ускорения или замедления, — условие, которое обнаруживается только на горизонтальной плоскости, ибо в случае движения по наклонной плоскости вниз уже существует причина ускорения, в то время, как при движении по наклонной плоскости вверх налицо замедление; из этого следует, что движение по горизонтальной плоскости вечно

Это суждение нельзя вывести непосредственно из эксперимента, так как невозможно исключить все внешние влияния (трение и т. п.). Поэтому, здесь Галилей впервые применил метод логического мышления, базирующийся на непосредственных наблюдениях и подобный математическому методу доказательства «от противного». Если наклон плоскости к горизонтали является причиной ускорения тела, движущегося по ней вниз, и замедления тела, движущегося по ней вверх, то при движении по горизонтальной плоскости у тела нет причин ускоряться или замедляться — и оно должно пребывать в состоянии равномерного движения или покоя.

Таким образом, Галилей просто и ясно доказал связь между силой и изменением скорости (ускорением), а не между силой и самой скоростью, как считали Аристотель и его последователи. Это открытие Галилея вошло в науку как закон инерции. Однако, Галилей допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). В 1638 году итальянец Балиани уточнил закон инерции, указав, что при полном отсутствии внешних воздействий естественной траекторией движения тела является прямая. В современном виде закон инерции сформулировал Декарт. Ньютон включил закон инерции в свою систему законов механики как первый закон.

Заключение

На протяжении всего времени своего существования человечество пытается понять явления, происходящие в природе. Попытки объяснить относительность движения были предприняты еще Галилео Галилеем. Исааку Ньютону удалось вывести закон инерции, который стали использовать в качестве основного постулата при проведении вычислений в механике.

В настоящее время в систему определения положения тела включают тело, прибор для определения времени, а также систему координат. В зависимости от того, подвижным или неподвижным является тело, можно дать характеристику положения определенного объекта в нужный промежуток времени.