Числа. действительные числа

Аргумент комплексного числа.

Полярный угол φ точки M (x, y) является аргументом комплексного числа z = x + iy. Обозначается как .

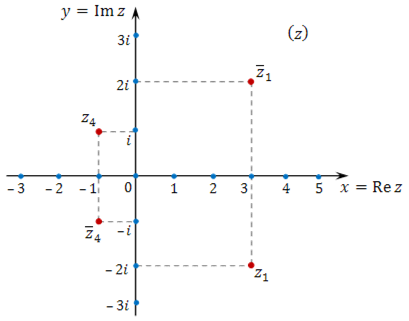
Формулу для определения аргумента комплексного числа z = x + iy, который задан в алгебраической форме, получаем, пользуясь связью декартовых и полярных координат точки M (x, y).

Для точек, которые не лежат на мнимой оси, то есть для z, у которых , получаем ; для точек мнимой положительной полуоси, то есть для z, у которых , получаем ; для точек мнимой отрицательной полуоси, то есть для z, у которых , получаем .

Аргумент числа  является величиной неопределенной.

Определение аргумента при  сводится к решению тригонометрического уравнения . При , то есть когда  является числом действительным, у нас есть  при  и  при .

При  решение уравнения зависимо от четверти плоскости . Четверть, в которое расположена точка z, определяют по знакам  и . В итоге имеем:

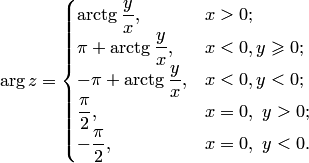
При решении примеров удобно пользоваться схемой:

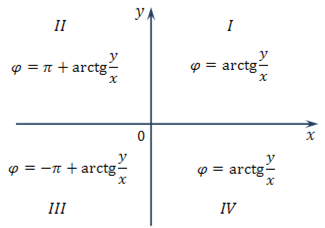
Пример. Найти аргументы чисел:

.

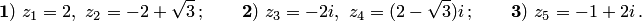Решим задачу для каждого из 3-х случаев:

1) числа  и  — действительные, причем , поэтому ;

2) числа  и  — чисто мнимые , причем  , поэтому  ;

3) для числа  имеем , поэтому из  находим ; так как при этом (точка  находится во второй четверти, то получаем  или .

Пример. Найти модуль и аргумент числа .

Основные виды чисел

Натуральные числа, получаемые при естественном счёте; множество натуральных чисел обозначается . Т.о. (иногда к множеству натуральных чисел также относят ноль, то есть ). Натуральные числа замкнуты относительно сложения и умножения (но не вычитания или деления). Натуральные числа коммутативны и ассоциативны относительно сложения и умножения, а умножение натуральных чисел дистрибутивно относительно сложения.

Целые числа, получаемые объединением натуральных чисел с множеством отрицательных чисел и нулём, обозначаются . Целые числа замкнуты относительно сложения, вычитания и умножения (но не деления).

Рациональные числа — числа, представленные в виде дроби m/n (n≠0), где m — целое число, а n — натуральное число. Для рациональных чисел определены все четыре «классические» арифметические действия: сложение, вычитание, умножение и деление (кроме деления на ноль). Для обозначения рациональных чисел используется знак .

Действительные (вещественные) числа представляют собой расширение множества рациональных чисел, замкнутое относительно некоторых (важных для математического анализа) операций предельного перехода. Множество вещественных чисел обозначается . Его можно рассматривать как пополнение поля рациональных чисел при помощи нормы, являющейся обычной абсолютной величины. Кроме рациональных чисел, включает множество иррациональных чисел , не представимых в виде отношения целых. Кроме подразделения на рациональные и иррациональные, действительные числа также подразделяются на алгебраические и трансцендентные. При этом каждое трансцендентное число является иррациональным, каждое рациональное число — алгебраическим.

Комплексные числа , являющиеся расширением множества действительных чисел. Они могут быть записаны в виде z = x + iy, где i — т. н. мнимая единица, для которой выполняется равенство i2 = − 1. Комплексные числа используются при решении задач квантовой механики, гидродинамики, теории упругости и пр.

Для перечисленных множеств чисел справедливо следующее выражение:

Простые числа — натуральные числа, которые в качестве множителей имеют только себя и единицу. Ряд простых чисел имеет вид: Любое натуральное число N можно представить в виде произведения степеней простых чисел: 121968=2^4*3^2*5^0*7^1*11^2. Это свойство широко используется в практической криптографии.

Действия над комплексными числами.

a + bi = c + di

означает, что a = c и b = d (2 комплексных числа равны между собой только в том случае, если равны их действительные и мнимые части).

Сложение.

(a + bi) + (c + di) = (a + c) + (b + d)i.

Для комплексных чисел работает правило 1-го класса: z₁ + z₂ = z₂ + z₁ – от перестановки слагаемых сумма не меняется.

Пример:

Сложим 2 комплексных числа z₁ = 1 + 3i, z2 = 4 – 5i.

Для того чтобы сложить 2 комплексных числа нужно сложить их действительные и мнимые части:

Вычитание.

(a + bi) – (c + di) = (a – c) + (b – d)i.

Пример:

Найдем разность комплексных чисел z₁ – z₂ и z₂ – z₁, с учетом того, что z₁ = -2 + i, .

Действие аналогично сложению, отличие только в том, что вычитаемое берем в скобки, а потом – как обычно раскрываем их со сменой знака:

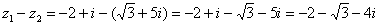
У числа, которое мы получили 2, а не 3 части. Так как действительная часть является составной: . Что было понятней ответ перепишем так: .

Рассчитываем 2-ю разность:

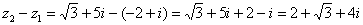
Здесь действительная часть тоже составная: .

Приведем короткий пример с «нехорошей» мнимой частью: . В этом случае без скобок никак не обойтись.

Умножение.

(a + bi)(c + di) = ac + bci + adi + bdi2 = (ac — bd) + (bc + ad)i.

Пример:

Найдем произведение комплексных чисел ,

Записываем произведение:

Раскрываем скобки, как обычно

Обратите внимание, что  и будьте внимательны

Напомним: Чтобы умножить многочлен на многочлен надо все члены 1-го многочлена умножить на каждый член другого многочлена.

Распишем подробно:

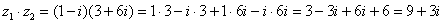
Очевидно, что .

Как и в сумме, в произведении комплексных чисел работает перестановочный закон: .

Произведение 2-х сопряжённых комплексных чисел равно положительному действительному  числу.

Деление.

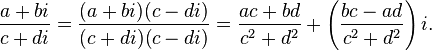
Разделить комплексное число  a + bi (делимое) на другое c + di (делитель) — значит найти третье число  e + fi  (частное), которое будучи умноженным на делитель c + di,  дает делимое  a + bi.

Если делитель ненулевой, деление всегда возможно.

Например:

Есть комплексные числа , . Найдем частное .

Составим частное:

Деление чисел производится способом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Напомним, что  и смотрим на наш знаменатель: . В знаменателе уже имеется , поэтому сопряженным выражением в данном случае оказывается , т.е. .

Из правила, знаменатель необходимо домножить на , и, чтобы ничего не изменилось, умножить числитель на такое же число :

Дальше в числителе раскрываем скобки. А в знаменателе пользуемся формулой  (при ).

Распишем пошагово:

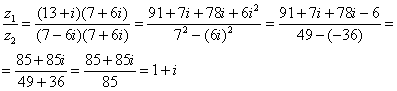
Часто перед делением дробь лучше упростить.

В частности,

Примеры решения задач

Пример 1

Задача

Записать множество

, если
, причём
= {2, 4, 6, 8, 10, 12},
= {3, 6, 9, 12}.

Решение

есть не что иное, как объединение множеств
и
, то есть, множество
будет состоять из элементов, принадлежащих как множеству
, так и множеству
:
= {2, 3, 4, 6, 8, 9, 10, 12}.

Ответ

Множество

состоит из элементов, которые принадлежат двум множествам
и
.

Пример 2

Задача

Все студенты курса изучают разные иностранные языки. Значит, из них, 91 студент изучает  английский язык, ещё 96 студентов изучают немецкий язык, 94 студента изучают исключительно французский язык, 36 студентов изучают не только английский, но и немецкий языки, ещё 32 студента изучают английский и французский языки, а 10 студентов занимаются изучением всех языков без исключения.

Вопрос: сколько студентов занимаются изучением немецкого и французского языков, если всего на курсе по списку 189 студентов?

Решение

Итак, для начала введём обозначения:

– множество всех студентов, которые находятся на данном курсе;

– множество студентов, которые изучают только английский язык;

– множество студентов, которые занимаются изучением немецкого языка;

– множество студентов, изучающих исключительно французский язык;

– множество студентов, которые изучают, как английский, так и немецкий язык;

– множество студентов, изучающие английский и французский языки;

– множество студентов, которіе изучают немецкий и французский язіки;

– множество студентов, которые изучают абсолютно все языки;

– количество элементов множества
.

По условию задачи:

Найдём

– количество студентов, которые изучают немецкий и французский языки. Согласно вышеописанному обозначению, у нас получается:

,
,
,
.

Из методов включения и исключения следует, что

.

Ответ

студента занимаются изучением немецкого и французского языков.

Математические действия

Существование математики невозможно без выполнения математических действий. Всего существует 4 вида арифметических действий:

Порядок выполнения математических действий в выражениях со скобками и без скобок

Так же имеется определенный порядок математических действий, запомнив который с легкостью можно решать задания любой сложности. Этот порядок зависит от наличия скобок и предложенных действий:

При отсутствии скобок, действия выполняются в обычном порядке. Вот правильный порядок математических действий в примере без скобок:

 24+16-5=35

1 действие: 24+16=40

2 действие: 40-5=35

В любом выражении первыми необходимо выполнить умножение или деление в порядке очереди. Вот правильный порядок арифметических действий без скобок:

 40-4×5+50=70

1 действие: 4×5=20

2 действие: 40-20=20

3 действие: 20+50=70 

Когда выражение содержит скобки, первыми вычисляются действия в скобках, а потом по порядку все остальные. Вот необходимый порядок математических действий в примере со скобками:

5+(20-10):2=10

1действие: 20-10=10

2 действие: 10:2=5

3 действие: 5+5=10

Все очень просто. Если сразу запомнить не получается, то можно пользоваться этим уроком, как шпаргалкой!

Следующий интересный момент заключается в том, что любой компонент математического действия имеет свое название:

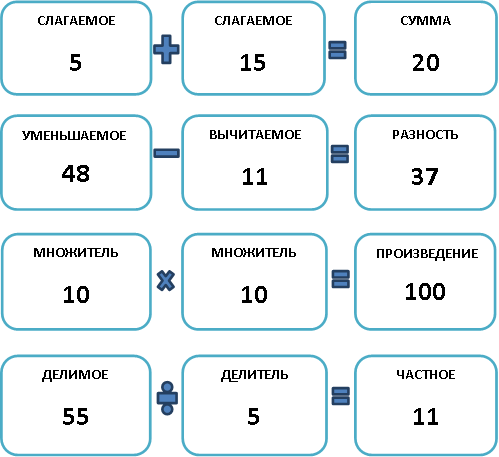
Правила нахождения неизвестного компонента при выполнении математических действий

Для того, чтобы максимально упростить решение задач и уравнений, существуют специальные правила нахождения неизвестного компонента:

1) Сложение:

— для нахождения одного из слагаемых необходимо от суммы отнять второе слагаемое:

Например:

?+48=50;

?=50-48=2.

2) Вычитание:

-для нахождения уменьшаемого достаточно найти сумму разности и вычитаемого:

Например:

?-25=50;

?=50+25+75.

-для нахождения вычитаемого, нужно от уменьшаемого отнять разность

Например:

44-?=10;

?=44-10=34.

3) Умножение:

— для нахождения множителя, необходимо найти частное произведения и второго множителя

Например:

?×6=48;

?=48:6=8.

4) Деление:

— для нахождения неизвестного делимого, необходимо найти произведение делителя и частного

Например:

?:11=3;

?=11×3=33.

— для нахождения неизвестного делителя, необходимо делимое разделить на частное

Например:                                                 

95:?=19;

?=95:19=5.

Число в философии

Философское понимание числа заложили пифагорейцы. Аристотель свидетельствует, что пифагорейцы считали числа «причиной и началом» вещей, а отношения чисел — основой всех отношений в мире. Числа придают миру упорядоченность и делают его космосом. Такое отношение к числу было принято Платоном, а позже неоплатониками. Платон при помощи чисел различает подлинное бытие (то, что существует и мыслится само по себе), и неподлинное бытие, (то, что существует лишь благодаря другому и познаётся только в отношении). Срединное положение между ними занимает число. Оно придаёт меру и определённость вещам и делает их причастными бытию. Благодаря числу вещи могут быть подвергнуты пересчёту и поэтому они могут быть мыслимы, а не только ощущаемы. Неоплатоники, особенно Ямвлих и Прокл, почитали числа столь высоко, что даже не считали их сущими — устроение мира исходит от числа, хотя и не непосредственно. Числа сверхсущны, пребывают выше Ума, и недоступны знанию. Неоплатоники различают божественные числа (прямую эманацию Единого) и математические числа (составленные из единиц). Последние являются несовершенными подобиями первых. Аристотель, наоборот, приводит целый ряд аргументов, показывающих, что утверждение о самостоятельном существовании чисел приводит к нелепостям. Арифметика выделяет в этих реально сущих вещах только один аспект и рассматривает их с точки зрения их количества. Числа и их свойства являются результатом такого рассмотрения. Кант считал, что явление познано тогда, когда оно сконструировано в соответствии с априорными понятиями — формальными условиями опыта. Число — одно из таких условий. Число задаёт конкретный принцип или схему конструирования. Любой объект является исчислимым и измеряемым, потому что он сконструирован по схеме числа (или величины). Поэтому всякое явление может рассматриваться математикой. Разум воспринимает природу подчинённой числовым закономерностям именно потому, что сам строит её в соответствии с числовыми закономерностями. Так объясняется возможность применения математики в изучении природы. Математические определения, разработанные в XIX веке, были серьёзно пересмотрены в начале XX века. Это было вызвано не столько математическими, сколько философскими проблемами. Определения, которые были даны Пеано, Дедекиндом или Кантором, и которые используются в математике и в настоящее время, нужно было обосновать с помощью фундаментальных принципов, коренящихся в самой природе знания. Различают три таких философско-математических подхода: логицизм, интуиционизм и формализм. Философскую базу логицизма разработал Рассел. Он полагал, что истинность математических аксиом неочевидна. Истинность обнаруживается сведением к наиболее простым фактам. Отражением таких фактов Рассел считал аксиомы логики, которые он положил в основу определения числа. Важнейшим понятием у него является понятие класса. Натуральное число η есть класс всех классов, содержащих η элементов. Дробь — это уже не класс, а отношение классов. Интуицист Брауэр имел противоположную точку зрения: логику он считал лишь абстракцией от математики, рассматривал натуральный ряд чисел как базовую интуицию, лежащую в основании всякой мыслительной деятельности. Гильберт, главный представитель формальной школы, видел обоснование математики в построении непротиворечивой аксиоматической базы, в пределах которой можно бы было формально обосновать любое математическое понятие. В разработанной им аксиоматической теории действительных чисел представление о числе лишается всякой глубины и сводится лишь к графическому символу, подставляемому по определённым правилам в формулы теории.

Что такое цифра?

Это вопрос, на который мы получаем ответ изначально от родителей, потом от преподавателей в учебных заведениях. Что такое цифра? А из словаря Владимира Даля можно узнать, что цифры — это численные показатели. Именно они представляются символами чисел. Нам известно всего 10 цифр: от нуля до девяти. Из их сочетания получается бесконечность чисел. Какие же существуют цифры?

• Арабские. Такими символами мы пользуемся довольно-таки давно. Они возникли в Европе еще в 10-м веке.
• Римские. Возникли еще за пять веков до нашей эры и находились в обиходе у племен этрусков, проживавших на Апеннинском полуострове.
• Цифры майя. Такие знаки использовались для расчетов в календаре.

Но в современном мире цифра — это не только математический знак, и сегодняшний день существует даже цифровое телевидение, а также существует цифровой формат.

В словаре Д.Н. Ушакова

ЧИСЛО́, числа, мн. числа, чисел, числам, ср.1. Понятие, служащее выражением количества, то, при помощи чего производится счет предметов и явлений (мат.). Целое число. Дробное число. Именованное число. Простое число. (см. простой1 в 1 ·знач. ). Теория чисел (отдел математики, изучающий общие свойства чисел).2. То же, что цифра в 1 ·знач. (·старин. ).3. Тот или иной день месяца в его порядковом ряду, месте (при названии месяца слово «число» в речи обычно опускается, напр. «первое мая» вместо «первое число мая»). Первого числа (·т.е. в первый день месяца) он возвращается из отпуска. Какое сегодня число? Какого числа твой день рождения? Пометить письмо задним числом (см. задний» title=’что такое задний, значение слова задний в словаре Ушакова’>задний), завтрашним, вчерашним числом. «Июня третьего числа коляска легкая в дорогу его по почте понесла.» Пушкин. «В последних числах сентября… в деревне скучно, грязь, ненастье.» Пушкин.4. только ед., кого-чего. Количество (кого-чего-нибудь, считаемого отдельными особями, единицами, штуками). Собралось большое число гостей. Число книг в библиотеке сильно возросло. Круглым числом (см. круглый» title=’что такое круглый, значение слова круглый в словаре Ушакова’>круглый в 3 ·знач. ). «Хлопочут набирать учителей полки, числом поболее, ценою подешевле.» Грибоедов.5. только ед. Совокупность, ряд известного количества кого-чего-нибудь. «А смешивать два эти ремесла есть тьма искусников, я не из их числа.» Грибоедов. В числе присутствующих не оказалось ни одного математика. Все дружно принялись за работу, и новички в том числе.6. Грамматическая категория, показывающая, об одном или о большем числе предметов идет речь (грам.). Единственное число. Двойственное число (указывает на два предмета). Множественное число (указывает на число предметов больше одного или, в языках, имеющих формы двойственного числа, — на число предметов больше двух). Изменяться в роде, числе и падеже.• Без числа — в очень большом количестве, в бесчисленном множестве. «У нас же дорога большая была: рабочего звания люди сновали по ней без числа.» Некрасов.

Свойства рациональных чисел.

Основные свойства рациональных чисел.

     1. Упорядоченность. Для всяких рациональных чисел a и b есть правило, которое позволяет однозначно идентифицировать между ними 1-но и только одно из 3-х отношений: «<», «>» либо «=». Это правило —  правило упорядочения и формулируют его вот так:

• 2 положительных числа a=m_a/n_a и b=m_b/n_b связаны тем же отношением, что и 2 целых числа m_a⋅n_b и m_b⋅n_a;
• 2 отрицательных числа a и b связаны одним отношением, что и 2 положительных числа |b| и |a|;
• когда a положительно, а b — отрицательно, то a>b.

∀a,b∈Q (a∨a>b∨a=b)

     2. Операция сложения. Для всех рациональных чисел a и b есть правило суммирования, которое ставит им в соответствие определенное рациональное число c. При этом само число c — это сумма чисел a и b и ее обозначают как (a+b), а процесс нахождения этого числа называют суммирование.

Правило суммирования выглядит так:

m_a/n_a+m_b/n_b=(m_a⋅n_b+m_b⋅n_a)/(n_a⋅n_b).

∀a,b∈Q ∃!(a+b)∈Q

     3. Операция умножения. Для всяких рациональных чисел a и b есть правило умножения, оно ставит им в соответствие определенное рациональное число c. Число c называют произведением чисел a и b и обозначают (a⋅b), а процесс нахождения этого числа называют умножение.

Правило умножения выглядит так: m_an_a⋅m_bn_b=m_a⋅m_bn_a⋅n_b.

∀a,b∈Q ∃(a⋅b)∈Q

     4. Транзитивность отношения порядка. Для любых трех рациональных чисел a, b и c если a меньше b и b меньше c, то a меньше c, а если a равно b и b равно c, то a равно c.

∀a,b,c∈Q (a∧b⇒a∧(a = b∧b = c ⇒ a = c)

     5. Коммутативность сложения. От перемены мест рациональных слагаемых сумма не изменяется.

∀a,b∈Q  a+b=b+a

     6. Ассоциативность сложения. Порядок сложения 3-х рациональных чисел не оказывает влияния на результат.

∀a,b,c∈Q  (a+b)+c=a+(b+c)

     7. Наличие нуля. Есть рациональное число 0, оно сохраняет всякое другое рациональное число при складывании.

∃∈Q ∀a∈Q  a+0=a

     8. Наличие противоположных чисел. У любого рационального числа есть противоположное рациональное число, при их сложении получается 0.

∀a∈Q ∃(−a)∈Q  a+(−a)=0

     9. Коммутативность умножения. От перемены мест рациональных множителей произведение не изменяется.

∀a,b∈Q  a⋅b=b⋅a

     10. Ассоциативность умножения. Порядок перемножения 3-х рациональных чисел не имеет влияния на итог.

∀a,b,c∈Q  (a⋅b)⋅c=a⋅(b⋅c)

     11. Наличие единицы. Есть рациональное число 1, оно сохраняет всякое другое рациональное число в процессе умножения.

∃1∈Q ∀a∈Q  a⋅1=a

     12. Наличие обратных чисел. Всякое рациональное число, отличное от нуля имеет обратное рациональное число, умножив на которое получим 1.

∀a∈Q ∃a−1∈Q  a⋅a−1=1

     13. Дистрибутивность умножения относительно сложения. Операция умножения связана со сложением при помощи распределительного закона:

∀a,b,c∈Q  (a+b)⋅c=a⋅c+b⋅c

     14. Связь отношения порядка с операцией сложения. К левой и правой частям рационального неравенства прибавляют одно и то же рациональное число.

∀a,b,c∈Q  a⇒a+c

     15. Связь отношения порядка с операцией умножения. Левую и правую части рационального неравенства можно умножить на одинаковое неотрицательное рациональное число.

∀a,b,c∈Q  c>0∧a⇒a⋅c⋅c

     16. Аксиома Архимеда. Каким бы ни было рациональное число a, легко взять столько единиц, что их сумма будет больше a.

Обобщения чисел

Кватернионы представляющие собой разновидность гиперкомплексных чисел. Множество кватернионов обозначается H{\displaystyle \mathbb {H} }. Кватернионы в отличие от комплексных чисел не коммутативны относительно умножения.

В свою очередь октавы O{\displaystyle \mathbb {O} }, являющиеся расширением кватернионов, уже теряют свойство ассоциативности.

В отличие от октав, седенионы S{\displaystyle \mathbb {S} } не обладают свойством альтернативности, но сохраняют свойство степенной ассоциативности.

Для этих множеств обобщённых чисел справедливо следующее выражение: C⊂H⊂O⊂S{\displaystyle \mathbb {C} \subset \mathbb {H} \subset \mathbb {O} \subset \mathbb {S} }

p-адические числа Qp{\displaystyle \mathbb {Q} _{p}} можно рассматривать как элементы поля, являющегося пополнением поля рациональных чисел Q{\displaystyle \mathbb {Q} } при помощи т. н. , аналогично тому, как поле действительных чисел R{\displaystyle \mathbb {R} } определяется как его пополнение при помощи обычной абсолютной величины.

Аде́ли определяются как бесконечные последовательности {a_∞,a₂,a₃,…a_p…}, где a_∞ — любое действительное число, а a_p — p-адическое, причём все a_p, кроме, может быть, конечного их числа, являются целыми p-адическими. Складываются и умножаются адели покомпонентно и образуют кольцо. Поле рациональных чисел вкладывается в это кольцо обычным образом r→{r, r,…r,…}. Обратимые элементы этого кольца образуют группу и называются иде́лями.

Практически важным обобщением числовой системы является интервальная арифметика.

В словаре Даля

ср. количество, счетом, на вопрос: сколько? и самый знак,
выражающий количество, цифра. Без числа; нет числа, без счету, многое
множество. Поставь приборы, по числу гостей. Числа римские, арабские или
церковные. Целое число, противопол. дробь. Четное число, что делится на
два без дроби. Круглым числом, средним. Число месяца, день, по счету,
счетом, начиная с первого до 31-го. Татарове реша: дайте нам число,
стар. счет населенью, перепись народа. Не с числа говоришь, вят. перм.
неверно, ошибочно, неправду. Число в число на тот месяц. Книга Чисел,
четвертая из пяти книг Моисеевых: счисленье еврейского народа, станов и
колен его, в пустыне. Занятия расписаны по числам (месяца). Все числом
да счетом. В том числе, в сем счету, в общем количестве. Числовой вывод,
в числах, в цифрах, количественный. Числить что, исчислять, считать,
рассчитывать, | считать в числе чего, полагать в счет. Его числят, он
числится в полку. Вычислить путь планеты. Дочислиться до вывода.
Зачислить кого на службу. Исчислить нужды свои. Начислить на кого долг.
Отчислять часть доходов в запас. Почислить дело решенным. Перечислить
кого в другое ведомство. Он причислен к министерству. Прочислил одну
статью, пропустил. Расчислить, почем придется на брата. Арифметики
счисляют мудреные задачи. Численье, действие по глаголу. Численные
величины, алгебр. означенные не буквами, а числами. — люди, стар.
податные, окладные. Численник стар. счетчик, переписчик народа русского,
от татар. Говори численно, вят. порядком, правильно, законно, верно.
Численность, число, счет чего, количество. Численность населенья все
растет. Числитель м. числящий, исчисляющий что. | Числитель, верхняя
цифра дроби, означающая, сколько частей взято от целого, разделенного на
столько частей, сколько единиц в знаменателе. Числительный, к числителю
относящ.; указывающий число чего либо. — имя, грамматич. слово,
означающее счет. Численка ж. тамб. тул. чисменка ниж. перм. олон.
чисменница костр. в мотке ниток, и в основе ткацкой, зубок; три нитки;
десять численок одна пасма; ниж. костр. чисменка четыре нитки или два
гнезда; вологодск. 20 чисменок, по 3 оборота, одна пасма; местами 40
чисменок пасма, в 120 ниток. Числовед или числослов, арифметик, счетчик.
Числословная, числоведная наука, числоведенье, числословие, арифметика,
математика, счетная наука.