Отрицательные числа

Наибольшее отрицательное и наименьшее положительное целое число

Со сравнением двух целых чисел мы полностью разобрались в предыдущих разделах этой статьи. Сейчас мы еще вкратце остановимся на сравнении трех и большего количества целых чисел, и разберем возникающие при этом ситуации.

Когда сравниваются три и более числа, то сначала проводится сравнение всех возможных пар, составленных из этих чисел. Например, при сравнении четырех целых чисел 7, 17, и −2 попарно сравниваются 7 и 17, 7 и , 7 и −2, 17 и , 17 и −2, и −2, при этом получаются следующие результаты 7<17, 7>0, 7>−2, 17>0, 17>−2 и 0>−2. После этого полученные результаты объединяются в цепочку неравенств (и равенств, когда есть равные числа). Для этого исходные числа записываются в порядке возрастания от самого меньшего до самого большего и между двумя соседними числами ставятся знак < (и знак = между равными числами). В нашем примере цепочка неравенств будет иметь следующий вид −2<0<7<17.

При сравнении нескольких чисел возникает понятие наибольшего и наименьшего числа.

Определение.

Число, которое меньше любого другого числа из рассматриваемого множества чисел, называется наименьшим числом в данном множестве.

Определение.

Число, которое больше любого другого числа в рассматриваемом множестве чисел, называется наибольшим числом в данном множестве.

Проще говоря, наибольшее число – это самое большое число в данном множестве чисел, а наименьшее число – это самое маленькое число.

Приведем пример наибольшего и наименьшего целого числа в множестве, состоящем из шести целых чисел −4, −81, −4, 17, и 17. Результат сравнения этих чисел имеет вид −81<−4=−4<0<17=17. Отсюда хорошо видно, что число −81 является наименьшим целым числом в рассматриваемом множестве, а число 17 – наибольшим целым числом в этом множестве.

Вообще все числа из множества целых чисел можно записать в порядке возрастания (каждое следующее число больше предыдущего), при этом получим последовательность целых чисел вида …, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, … Эту последовательность целых чисел можно также записать в виде бесконечной цепочки неравенств: …<−5<−4<−3<−2<−1<0<1<2<3<4<5<…

Отсюда видно, что в множестве целых чисел не существует ни наибольшего целого числа, ни наименьшего целого числа. Действительно, всегда можно указать целое число, которое больше любого наперед заданного сколь угодно большого целого числа (им будет любое следующее число в последовательности целых чисел). Аналогично можно указать целое число, которое меньше любого наперед заданного сколь угодно малого целого числа (это любое число, предшествующее заданному числу в последовательности целых чисел).

Однако во множестве целых положительных чисел (1, 2, 3, …) существует наименьшее целое число – это число 1. Во множестве целых неотрицательных чисел (0, 1, 2, 3, …) наименьшим числом является число . Целое положительное число в только что указанных множествах мы указать не можем.

Число нуль является наибольшим целым неположительным числом (во множестве целых неположительных чисел …, −3, −2, −1, 0). А −1 (минус один) – это наибольшее целое число в множестве целых отрицательных чисел (…, −3, −2, −1). Наименьшего целого числа эти множества не имеют.

Список литературы.

Некогда разбираться?

Примеры сравнения отрицательных чисел

Разберем решения нескольких примеров сравнения отрицательных чисел.

Начнем со сравнения двух отрицательных целых чисел. Это самый простой из возможных случаев сравнения отрицательных чисел, на нем проще всего усвоить суть правила сравнения отрицательных чисел.

Пример.

Сравните отрицательные числа −38 и −7.

Решение.

Воспользуемся правилом сравнения отрицательных чисел. Оно нам указывает, что сначала нужно найти модули данных чисел, после чего провести сравнение полученных положительных чисел.

Модули сравниваемых чисел равны 38 и 7 соответственно. Сравнив натуральные числа 38 и 7, получаем, что 38>7. Следовательно, −38 меньше, чем −7, так как модуль числа −38 больше, чем модуль числа −7.

Ответ:

−38<−7.

Немного сложнее дела обстоят со сравнением отрицательных рациональных чисел. Сравнение таких чисел сводится либо к сравнению обыкновенных дробей, либо к сравнению десятичных дробей.

Пример.

Какое из отрицательных чисел и −3,7 больше?

Решение.

Придерживаясь правила сравнения отрицательных чисел, сначала находим модули сравниваемых чисел, имеем и 3,7.

Теперь можно перевести числа в обыкновенные дроби, после чего выполнить сравнение.
Так смешанное число соответствует дроби , еще выполним : . Осталось выполнить и . Приведем их к общему знаменателю: и , теперь видно, что , таким образом, . Следовательно, , откуда заключаем, что . То есть, из двух исходных отрицательных чисел большим является .

Заметим, что сравнение чисел и 3,7 можно было выполнить и иначе, выполнив перевод смешанного числа в десятичную дробь с последующим сравнением десятичных дробей. Так как и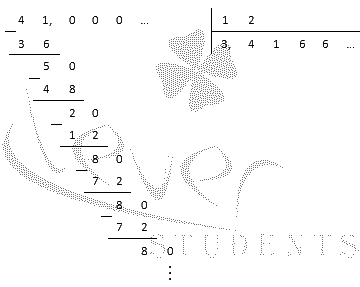
то (при необходимости смотрите ). Очевидно, 3,41(6)<3,7, следовательно, . Отсюда заключаем, что из отрицательных чисел и −3,7 больше .

Ответ:

.

Сравнение отрицательных действительных чисел проводится по тому же правилу сравнения отрицательных чисел, примеры можно посмотреть в статье сравнение действительных чисел.

Список литературы.

• Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
• Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
• Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).

Некогда разбираться?

Равные и неравные целые числа

Результатом сравнения двух целых чисел может быть один из выводов: либо эти числа равны, либо – не равны. Для начала дадим определение равных и неравных целых чисел.

Определение.

Два целых числа называются равными, если их записи совпадают вплоть до знаков, или если это целые числа и −0 (−0 это есть не что иное, как ). В противном случае целые числа называются неравными.

Отдельно скажем о равенстве целых чисел и −0. Число −0 есть противоположное число нулю, а число, противоположное нулю, есть нуль.

На основании приведенного определения мы легко можем выяснить, равны ли два заданных целых числа. Например, целые числа −95 и −95 равны, так как их записи одинаковы и знаки тоже, целые числа −1 и 1 не равны, так как их знаки различны, целые числа 148 и −90 312 также не равны, так как их записи и знаки различны.

Для записи равных чисел используют знак равно вида «=», который располагают между равными числами. Например, равенство целых чисел −51 и −51 можно записать как −51=−51, с другой стороны запись −767=−767 означает равенство целых чисел −767 и −767. Также для краткости записи используется знак не равно вида «≠». К примеру, запись 54≠−61 означает, что целые числа 54 и −61 не равны.

Приведем еще одну более строгую формулировку определения равных и неравных целых чисел, в которой фигурирует модуль числа.

Определение.

Два целых числа равны между собой, если эти числа имеют одинаковые знаки и равны модули этих чисел, а также, если это целые числа и −0. В противном случае два целых числа не равны.

Приведем пример использования этого определения для выяснения равенства или неравенства двух целых чисел.

Рассмотрим пример. Выясним, равны ли целые числа −708 и −711. Оба числа имеют знак минус, поэтому переходим к сравнению модулей этих целых чисел. Модуль числа −708 равен 708, а , и натуральные числа 708 и 711 не равны (при необходимости смотрите раздел теории ). То есть, модули сравниваемых целых чисел не равны, следовательно, −708≠−711.

Разберем еще один пример. Целые числа 11 и 11 равны, так как знаки сравниваемых целых чисел одинаковы (оба числа 11 и 11 со знаком плюс), и модулями этих чисел являются равные натуральные числа 11 и 11. Отметим, что можно было рассуждать и так: сравниваемые целые числа 11 и 11 являются натуральными числами, причем их записи одинаковы, значит, они равны.

В случае неравенства двух чисел обычно принято уточнять, какое из чисел больше, а какое – меньше другого. Ниже мы разберем правила, позволяющие это делать.

Сравнение положительных чисел с нолем

Чтобы не испытывать трудностей при выполнении сравнения положительных чисел и нуля, давайте рассмотрим задачу.

У Марины в кармане было четыре конфеты, а в Наташином кармашке лежало 0 конфет. Подумайте и объясните, у кого из девочек имелось большее количество конфет.

Изучив условие задачи, мы понимаем, что для ответа на главный вопрос задачи нужно выполнить сравнение количества Марининых сладостей с количеством сладостей, имеющихся у Натальи, то есть 4 и 0.

Давайте определим, к каким числам можно отнести значение четыре? К положительным или отрицательным?

Вспомним определение положительного:

Положительными числами называют числа со знаком +.На письме, не принято ставить знак «плюс» перед положительными числами. Считается, что если перед числом не стоит знак «минус», то число является положительным.

Исходя из определения, рассматриваемое значение считается положительным.

Переходим ко второму числу: 0.

Обязательно нужно понимать, что такое 0.

0 является целым числом, но при этом, не обозначает количество предметов.

Если будем рассматривать ноль в обычной жизни, то можно сказать иначе: 0 = «ничего».

Например:

в кассе 0 рублей = касса пуста, денег нет;

улов дедушки составил 0 рыб = дедушка ничего не поймал;

мальчик вынес во двор 0 игрушек = мальчик не вынес во двор игрушки.

Делаем вывод, что у Наташи не было конфет, а у Марины было 4 леденца.

Теперь можно выполнить сравнение положительного числа 4 с числом 0.

Даже ребенок понимает, что четыре конфетки больше, чем ничего или 0.

Значит, 4 > 0.

Из рассмотренного пояснения следует:

любое положительное число всегда будет больше, чем ноль!

Например:

1>0;

866>0;

15>0.

Описание изменения величин при помощи целых чисел

Пришло время поговорить о том, для чего вообще нужны целые числа.

Основное предназначение целых чисел заключается в том, что с их помощью удобно описывать изменение количества каких-либо предметов. Разберемся с этим на примерах.

Пусть на складе находится некоторое количество деталей. Если на склад привезут еще, к примеру, 400 деталей, то количество деталей на складе увеличится, а число 400 выражает это изменение количества в положительную сторону (в сторону увеличения). Если же со склада заберут, например, 100 деталей, то количество деталей на складе уменьшится, а число 100 будет выражать изменение количества в отрицательную сторону (в сторону уменьшения). На склад не будут привозить детали, и не будут увозить детали со склада, то можно говорить о неизменности количестве деталей (то есть можно будет говорить о нулевом изменении количества).

В приведенных примерах изменение количества деталей можно описать при помощи целых чисел 400, −100 и соответственно. Положительное целое число 400 показывает изменение количества в положительную сторону (увеличение). Отрицательное целое число −100 выражает изменение количества в отрицательную сторону (уменьшение). Целое число показывает, что количество осталось без изменения.

Удобство использования целых чисел по сравнению с использованием натуральных чисел заключается в том, что не нужно явно указывать увеличивается количество или уменьшается, — целое число определяет изменение количественно, а знак целого числа указывает направление изменения.

Целые числа также могут выражать не только изменение количества, но и изменение какой-либо величины. Разберемся с этим на примере изменения температуры.

Повышение температуры, скажем, на 4 градуса выражается положительным целым числом 4. Понижение температуры, например, на 12 градусов можно описать отрицательным целым числом −12. А неизменность температуры – это ее изменение, определяемое целым числом .

Отдельно нужно сказать о трактовке отрицательных целых чисел как величины долга. Например, если у нас есть 3 яблока, то целое положительное число 3 показывает количество яблок, которыми мы владеем. С другой стороны, если мы должны кому-либо отдать 5 яблок, а у нас их нет в наличии, то эту ситуацию можно описать при помощи отрицательного целого числа −5. В этом случае мы «обладаем» −5 яблоками, знак минус указывает на долг, а число 5 определяет долг количественно.

Понимание отрицательного целого числа в качестве долга позволяет, например, обосновать . Приведем пример. Если кто-то должен 2 яблока одному человеку и одно яблоко – другому, то общий долг составляет 2+1=3 яблока, поэтому −2+(−1)=−3.

Список литературы.

Некогда разбираться?

Сравнение числовых значений с использованием горизонтальной координатной прямой

Ну а теперь, рассмотрим еще одни способ сравнения цифровых записей с разными знаками.

Давайте начертим координатную прямую. Для этого, вспомним, что представляет собой координатная прямая.

Координатная прямая – прямая линия, имеющая направление, точку начала отсчета и единичный отрезок.

Отметим на прямой точки A(-4), C(-2), B(2),D(3).

Помни!Точки с положительным значением координаты расположены справа от точки начала отсчета, точки с отрицательным значением координаты находятся слева от точки начала отсчета.

И теперь, с помощью горизонтальной координатной прямой давайте рассмотрим математическое действие – сравнение чисел.

Сравнение положительных и отрицательных чисел с помощью координатной прямой.

Мы знаем, что точки с положительными координатами, расположились справа от точки начала отсчета, а с отрицательными слева. На координатную прямую нанесены точки B и D, имеющие координаты со знаком «плюс». Сравним координаты данных точек.

2<3 – два меньше трех. Получается, чем правее расположена точка на координатной прямой, тем большее числовое значение будет иметь её координата. Верно и обратное утверждение, чем левее на координатной прямой находится точка, тем меньшим будет цифровое выражение её координаты. Данное правило является верным и для записей со знаком «минус».

Например:

Точка A(-4) находится левее точки C (-2). А нам известно, чем левее расположена точка на координатной прямой, тем меньшее цифровое значение будет иметь её координата. Давайте проверим данное утверждение. Для этого сравним значение координат -2 и -4.

Из двух цифровых записей со знаком «минус», большим будет та, чей модуль окажется меньшим. Найдем модули.

-2=|2|;

-4=|4|.

Сравним значение модулей: 2<4.

Выходит, что -2 имеет меньший модуль, чем -4, следовательно, большее числовое значение -2>-4.

Сравнение положительных чисел с нолем с помощью координатной прямой.

Используя рассмотренное правило, делаем вывод, что точка с любой положительной координатой,  находится на координатной прямой,  правее точки начала отсчета, а значит,  имеет большее числовое значение.

То есть, ноль всегда меньше любого положительного числа.

Сравнение отрицательных чисел с нолем с помощью координатной прямой.

Любая точка, имеющая отрицательное значение координаты, всегда будет расположена левее точки 0, следовательно, любая числовая запись со знаком «минус» всегда меньше 0.

Сравнивать очень просто и интересно, главное запомнить простые правила сравнения и верно использовать их при выполнении заданий!

Координатная прямая

Координатная прямая это прямая линия, на которой располагаются все числа: и отрицательные и положительные. Выглядит следующим образом:

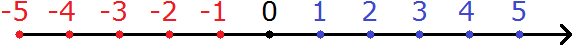
Здесь показаны только числа от −5 до 5. На самом деле координатная прямая бесконечна. На рисунке представлен лишь её небольшой фрагмент.

Числа на координатной прямой отмечают в виде точек. На рисунке жирная чёрная точка является началом отсчёта. Начало отсчёта начинается с нуля. Слева от начала отсчёта отмечают отрицательные числа, а справа — положительные.

Координатная прямая продолжается бесконечно по обе стороны. Бесконечность в математике обозначается символом ∞. Отрицательное направление будет обозначаться символом −∞, а положительное символом +∞. Тогда можно сказать, что на координатной прямой располагаются все числа от минус бесконечности до плюс бесконечности:

(−∞; +∞)

Каждая точка на координатной прямой имеет своё имя и координату. Имя — это любая латинская буква. Координата — это число, которое показывает положение точки на этой прямой. Проще говоря, координата это то самое число, которое мы хотим отметить на координатной прямой.

Например, точка А(2) читается как «точка А с координатой 2 и будет обозначаться на координатной прямой следующим образом:

Здесь A — это имя точки, 2 — координата точки A.

Пример 2. Точка B(4) читается как «точка B с координатой 4 и будет обозначаться на координатной прямой так:

Здесь B — это имя точки, 4 — координата точки B.

Пример 3. Точка M(−3) читается как «точка M с координатой минус три» и будет обозначаться на координатной прямой так:

Здесь M — это имя точки, −3 — координата точки M.

Точки можно обозначать любыми буквами. Но общепринято обозначать их большими латинскими буквами. Более того, начало отчёта, которое по другому называют началом координат принято обозначать большой латинской буквой O

Легко заметить, что отрицательные числа лежат левее относительно начала отсчёта, а положительные числа правее.

Существуют такие словосочетания как «чем левее, тем меньше» и «чем правее, тем больше». Наверное, вы уже догадались о чём идёт речь. При каждом шаге влево число будет уменьшаться в меньшую сторону. И при каждом шаге вправо число будет увеличиваться. Стрелка, направленная вправо, указывает на положительное направление отсчёта.