Числа мерсенна проект 5 класс
Содержание:
Описание
x будем обозначать векторы-слова, которые представляют собой w-мерные векторы над полем F2{\displaystyle F_{2}} = {0,1} , соответствующие машинному слову размера w.
Вихрь Мерсенна генерирует последовательность вектор-слов, которые являются псевдослучайными целыми из диапазона от 0 до 2w — 1. Путём деления на 2w — 1 мы получим псевдослучайное вещественное из диапазона .
Алгоритм основан на следующем рекуррентном выражении:
- xk+n:=xk+m⊕(xku∣xk+1l)A(1)k=,1,…{\displaystyle x_{k+n}:=x_{k+m}\oplus ({x_{k}}^{u}\mid {x_{k+1}}^{l})A\qquad (1)\qquad k=0,1,\ldots }
Где:
- n-целое, которое обозначает степень рекуррентности
- m-целое, 1 ≤ m ≤ n
- A— матрица размера w×w, с элементами из F2{\displaystyle F_{2}}.
- ∣{\displaystyle \mid } — Побитовое ИЛИ (OR)
- ⊕{\displaystyle \oplus } — Сложение по модулю два (XOR)
В правой части xku обозначает «старшие w-r бит» xk и xk+1l ≪младшие r бит≫ xk+1. Вектор (xku | xk+1l) является конкатенацией старших w-r бит xk и младших r бит xk+1. Возьмём (x, x1,…, xn-1) в качестве начального заполнения. Тогда генератор вычислит xn по рекуррентному выражению при k= 0. Полагая k = 1,2, …, генератор вычислит xn+1, xn+2,…
Форма матрицы A выбрана из расчета скорости выполнения умножения на A:
A=(11⋯⋯⋱⋱1aw−1aw−2⋯⋯⋯a){\displaystyle A={\begin{pmatrix}0&1&&&&\\0&0&1&&&\\0&\cdots &\cdots &\ddots &&\\&&&&\ddots &\\&&&&&1\\a_{w-1}&a_{w-2}&\cdots &\cdots &\cdots &a_{0}\end{pmatrix}}}
И вычисление xA сводится к побитовым операциям:
xA={x≫1x=(x≫1)⊕ax=1{\displaystyle {\boldsymbol {x}}A={\begin{cases}{\boldsymbol {x}}\gg 1&x_{0}=0\\({\boldsymbol {x}}\gg 1)\oplus {\boldsymbol {a}}&x_{0}=1\end{cases}}}
Где
- x:=(xku∣xk+1l)k=,1,…{\displaystyle {\boldsymbol {x}}:=({x_{k}}^{u}\mid {x_{k+1}}^{l})\qquad \qquad k=0,1,\ldots }
- a:=(aw−1,aw−2,…,a){\displaystyle {\boldsymbol {a}}:=({a_{w-1}},{a_{w-2}},\ldots ,{a_{0}})}
- x:=(xw−1,xw−2,…,x){\displaystyle {\boldsymbol {x}}:=({x_{w-1}},{x_{w-2}},\ldots ,{x_{0}})}
Неполные массивы
Неполные массивы
Последовательность МТ (xk+n, xk+n-1,…, xk+1u) образует (n × w — r)-массив. Так как r битов отбрасываются, массив называется неполным массивом. Каждый элемент получен из рекуррентного соотношения (1). Смена состояния MT также происходит по линейному соотношению и определяется с помощью линейного преобразования B.
В соответствии с общей теорией линейных рекуррентных последовательностей, каждое значение в (n × w − r)-массиве есть линейная рекуррентная последовательность, соответствующая характеристическому многочлену φB(t) преобразования B.
Матрица B имеет размеры (n × w − r) × (n × w − r) и следующую форму:
B=(Iw⋯⋮Iw⋮⋱⋮⋮⋮⋯Iw⋯Iw−rS⋯)←m-th row{\displaystyle B={\begin{pmatrix}0&I_{w}&\cdots &0&0\\\vdots &&&&\\I_{w}&\vdots &\ddots &\vdots &\vdots \\\vdots &&&&\\0&0&\cdots &I_{w}&0\\0&0&\cdots &0&I_{w-r}\\S&0&\cdots &0&0\end{pmatrix}}{\begin{matrix}\\\\\leftarrow m{\hbox{-th row}}\\\\\\\\\end{matrix}}}
S=(IrIw−r)A{\displaystyle S={\begin{pmatrix}0&I_{r}\\I_{w-r}&0\end{pmatrix}}A}
Где Ir{\displaystyle I_{r}} — единичная матрица размера r × r.
Для l=,1,…{\displaystyle l=0,1,\ldots } выполняется (xl+n,xl+n−1,…,xl+1):=(xl+n−1,xl+n−2,…,xl)B{\displaystyle (x_{l+n},x_{l+n-1},\ldots ,x_{l+1}):=(x_{l+n-1},x_{l+n-2},\ldots ,x_{l})B}.
Характеристический многочлен φB(t) преобразования B имеет вид:
φB(t) = (tn + tm)w-r × (tn-1 + tm-1)r + a(tn + tm)w-r × (tn-1 + tm-1)r-1 + … + ar-2(tn + tm)w-r × (tn-1 + tm-1) + ar-1(tn + tm)w-r + ar(tn + tm)w-r-1 + … + aw-2(tn + tm) + aw-1
Последовательность достигает максимального периода 2(nw-r)−1, тогда и только тогда когда φB(t) -примитивный.
Закалка
Необработанные последовательности, генерируемые рекурсией (1), обладают плохим равномерным распределением на больших размерностях. Чтобы это исправить, используется метод закалки (англ. tempering), на выходе которого получается итоговая псевдослучайная последовательность. Метод заключается в том, что каждое сгенерированное слово умножается справа на специальную обратимую матрицу T размера w × w. Для матрицы T: x → z = x T, выбраны следующие последовательные преобразования:
- y := x ⊕ (x >> u)
- y := :y ⊕ ((y << s) & b)
- y := :y ⊕ ((y << t) & c)
- z := y ⊕ (y >> l)
где l, s, t и u — целые, а b и c — специально подобранные битовые маски размера слова, и (x≫u) обозначает побитовую операцию сдвига вправо на u бит.
Conjectures and Unsolved Problems
- Is there an odd perfect number?
- We know that all even perfect numbers are a Mersenne prime times a power
of two (), but what about odd perfect
numbers? If there is one, then it is a perfect square times an odd
power of a single prime; it is divisible by at least eight primes and
has at least 75 prime factors (not necessarily distinct ,
,
) with at least 9 distinct ;
it has at least 300 decimal digits ; and it has a prime divisor greater
that 1020 . For more information see or . - Are there infinitely many Mersenne primes?
- Equivalently we could ask: Are there infinitely many even perfect numbers?
The answer is probably yes (because the harmonic series diverges). - Are there infinitely many Mersenne composites?
- Euler showed:
So if p=4k+3 and 2p+1 are prime then the Mersenne number
2p-1 is composite (and it seems reasonable to conjecture that
there are infinitely many primes pairs such p, 2p+1). - The New Mersenne Conjecture:
- Bateman, Selfridge and Wagstaff have conjectured the following.
Notice how this conjecture is related to the theorem in the previous conjecture.
See our page on The New Mersenne Conjecture for status information. - Is every Mersenne number 2p-1 square free?
- This falls more in the category of an open question (to which we do not
know the answer), rather than a conjecture (which we guess is true) . It is easy
to show that if the square of a prime p divides a Mersenne, then p is a Wieferich
prime and these are rare! Only two are known below 4,000,000,000,000
and neither of these squared divide a Mersenne. - Let C = 2, then let C1 = 2C-1,
C2 = 2C1-1, C3 = 2C2-1,
… Are these all prime? - According to Dickson Catalan responded in 1876 to Lucas’ stating 2127-1 (C4)
is prime with this sequence. These numbers grow very quickly:
It seems very unlikely that C5 (or many of the larger terms) would
be prime, so this is no doubt another example of Guy’s strong law of small
numbers. Notice that if there is even one composite term in this
sequences, then by all of the following
terms are composite.
(Landon Curt Noll tells
me he has used his program calc to verify that C5 has no prime divisors below 5*1051.) - Are there more double-Mersenne primes?
- Another common early misconception was that if n=Mp is prime, then so is Mn; lets call this number MMp (a «double-Mersenne»). Indeed each of the first four such numbers are
prime:However, the next four (MM13 MM17 MM19 and
MM31) all have known factors—so are composite. Are there
any more primes in this sequence? Probably not, but it remains an open
question. Tony Forbes is leading a
project to search for a factor of the next term: MM61, you
might want to join and help!Notice the above is a subsequence of
this one.
Early History
Many early writers felt that the numbers of the form 2n-1 were
prime for all primes n, but in 1536 Hudalricus Regius showed that
211-1 = 2047 was not prime (it is 23.89). By 1603 Pietro
Cataldi had correctly verified that 217-1 and 219-1
were both prime, but then incorrectly stated 2n-1 was also
prime for 23, 29, 31 and 37. In 1640 Fermat showed Cataldi was wrong about 23 and 37; then Euler in 1738 showed Cataldi was also wrong about 29. Euler showed Cataldi’s assertion about 31 was correct.
Enter French monk Marin Mersenne (1588-1648). Mersenne stated in the preface to his Cogitata Physica-Mathematica (1644) that the numbers 2n-1 were prime for
and were composite for all other positive integers n < 257. Mersenne’s
(incorrect) conjecture fared only slightly better than Regius’, but still got
his name attached to these numbers.
It was obvious to Mersenne’s peers that he could not have tested all of these
numbers (in fact he admitted as much), but they could not test them either.
It was not until over 100 years later, in 1750, that Euler verified the next number
on Mersenne’s and Regius’ lists, 231-1, was prime. After another
century, in 1876, Lucas verified 2127-1 was also prime. Seven years later Pervouchine showed 261-1 was prime, so Mersenne had missed this one. In the early 1900’s Powers showed that Mersenne had also missed the primes 289-1 and 2107-1. Finally, by 1947 Mersenne’s range, n < 258, had been completely checked and it was determined that the correct list is:
See the primes below.
Алгоритм
Вихрь Мерсенна алгоритмически реализуется двумя основными частями: рекурсивной и закалки. Рекурсивная часть представляет собой регистр сдвига с линейной обратной связью, в котором все биты в его слове определяются рекурсивно; поток выходных битов определяются также рекурсивно функцией битов состояния.
Блок-схема.
Регистр сдвига состоит из 624 элементов, и, в общей сложности, из 19937 клеток. Каждый элемент имеет длину 32 бита за исключением первого элемента, который имеет только 1 бит за счет отбрасывания бита.
Процесс генерации начинается с логического умножения на битовую маску, отбрасывающей 31 бита (кроме наиболее значащих).
Следующим шагом выполняется инициализация (x, x1,…, x623) любыми беззнаковыми 32-разрядными целыми числами. Следующие шаги включают в себя объединение и переходные состояния.
Смена состояния МТ.
Пространство состояний имеет 19937 бит (624·32 — 31). Следующее состояние генерируется сдвигом одного слова вертикально вверх и вставкой нового слова в конец. Новое слово вычисляется гаммированием средней части с исключённой. Выходная последовательность начинается с x624, x625,…
Алгоритм производится в шесть этапов:
Шаг 0. Предварительно инициализируется значение констант u, h, a u ← 10…0 битовая маска старших w-r бит, h ← 01…1 битовая маска младших r бит, a ← aw-1aw-2…a последняя строка матрицы A.Шаг 1. x, x,…,x ← начальное заполнениеШаг 2. Вычисление (xiu | xi+1l) y ← (x AND u1) OR (x AND h1)Шаг 3. Вычисляется значение следующего элемента последовательности по рекуррентному выражению (1) x ← x XOR (y>>1) XOR a если младший бит y = 1 Или x ← x XOR (y>>1) XOR 0 если младший бит y = 0 Шаг 4. Вычисление xT y ← x y ← y XOR (y>>u) y ← y XOR ((y<<s) AND b) y ← y XOR ((y<<t) AND c) z ← y XOR (y>>l) вывод z Шаг 5. i ← (i + 1) mod n Шаг 6. Перейти к шагу 2.
Table of Known Mersenne Primes
Let M(p) = 2p-1 and P(p) = 2p-1(2p-1).
The list of all known primes p for which M(p) is a Mersenne prime
(therefore P(p) is a perfect number) follows:
| ## |
p (exponent) |
digits in Mp |
digits in Pp |
year | discoverer | notes |
|---|---|---|---|---|---|---|
| 1 | 2 | 1 | 1 | —- | —- | |
| 2 | 3 | 1 | 2 | —- | —- | |
| 3 | 5 | 2 | 3 | —- | —- | |
| 4 | 7 | 3 | 4 | —- | —- | |
| 5 | 13 | 4 | 8 | 1456 | anonymous | |
| 6 | 17 | 6 | 10 | 1588 | Cataldi | |
| 7 | 19 | 6 | 12 | 1588 | Cataldi | |
| 8 | 31 | 10 | 19 | 1772 | Euler | |
| 9 | 61 | 19 | 37 | 1883 | Pervushin | |
| 10 | 89 | 27 | 54 | 1911 | Powers | |
| 11 | 107 | 33 | 65 | 1914 | Powers | note |
| 12 | 127 | 39 | 77 | 1876 | Lucas | |
| 13 | 521 | 157 | 314 | 1952 | Robinson | |
| 14 | 607 | 183 | 366 | 1952 | Robinson | |
| 15 | 1279 | 386 | 770 | 1952 | Robinson | |
| 16 | 2203 | 664 | 1327 | 1952 | Robinson | |
| 17 | 2281 | 687 | 1373 | 1952 | Robinson | |
| 18 | 3217 | 969 | 1937 | 1957 | Riesel | |
| 19 | 4253 | 1281 | 2561 | 1961 | Hurwitz | |
| 20 | 4423 | 1332 | 2663 | 1961 | Hurwitz | |
| 21 | 9689 | 2917 | 5834 | 1963 | Gillies | |
| 22 | 9941 | 2993 | 5985 | 1963 | Gillies | |
| 23 | 11213 | 3376 | 6751 | 1963 | Gillies | |
| 24 | 19937 | 6002 | 12003 | 1971 | Tuckerman | |
| 25 | 21701 | 6533 | 13066 | 1978 | Noll & Nickel | |
| 26 | 23209 | 6987 | 13973 | 1979 | Noll | « |
| 27 | 44497 | 13395 | 26790 | 1979 | Nelson & Slowinski | |
| 28 | 86243 | 25962 | 51924 | 1982 | Slowinski | |
| 29 | 110503 | 33265 | 66530 | 1988 | Colquitt & Welsh | |
| 30 | 132049 | 39751 | 79502 | 1983 | Slowinski | |
| 31 | 216091 | 65050 | 130100 | 1985 | Slowinski | |
| 32 | 756839 | 227832 | 455663 | 1992 | Slowinski & Gage et al. | (web page) |
| 33 | 859433 | 258716 | 517430 | 1994 | Slowinski & Gage | |
| 34 | 1257787 | 378632 | 757263 | 1996 | Slowinski & Gage | (web page) |
| 35 | 1398269 | 420921 | 841842 | 1996 | Armengaud, Woltman, et al. (GIMPS) | (web page) |
| 36 | 2976221 | 895932 | 1791864 | 1997 |
Spence, Woltman, et al. (GIMPS) |
(web page) |
| 37 | 3021377 | 909526 | 1819050 | 1998 |
Clarkson, Woltman, Kurowski et al. (GIMPS, PrimeNet) |
(web page) |
| 38 | 6972593 | 2098960 | 4197919 | 1999 |
Hajratwala, Woltman, Kurowski et al. (GIMPS, PrimeNet) |
(web page) |
| 39 | 13466917 | 4053946 | 8107892 | 2001 |
Cameron, Woltman, Kurowski et al. (GIMPS, PrimeNet) |
(web page) |
| 40 | 20996011 | 6320430 | 12640858 | 2003 |
Shafer, Woltman, Kurowski et al. (GIMPS, PrimeNet) |
(web page) |
| 41 | 24036583 | 7235733 | 14471465 | 2004 |
Findley, Woltman, Kurowski et al. (GIMPS, PrimeNet) |
(web page) |
| 42 | 25964951 | 7816230 | 15632458 | 2005 |
Nowak, Woltman, Kurowski et al. (GIMPS, PrimeNet) |
(web page) |
| 43 | 30402457 | 9152052 | 18304103 | 2005 |
Cooper, Boone, Woltman, Kurowski et al. (GIMPS, PrimeNet) |
(web page) |
| 44 | 32582657 | 9808358 | 19616714 | 2006 | Cooper, Boone, Woltman, Kurowski et al. (GIMPS, PrimeNet) |
(web page) |
| 45 | 37156667 | 11185272 | 22370543 | 2008 | Elvenich, Woltman, Kurowski et al. (GIMPS, PrimeNet) |
(web page) |
| 46 | 42643801 | 12837064 | 25674127 | 2009 | Strindmo, Woltman, Kurowski et al. (GIMPS, PrimeNet) |
(web page) |
| 47 | 43112609 | 12978189 | 25956377 | 2008 | Smith, Woltman, Kurowski et al. (GIMPS, PrimeNet) |
(web page) |
| 48? | 57885161 | 17425170 | 34850339 | 2013 | Cooper, Woltman, Kurowski et al. (GIMPS, PrimeNet) |
(web page) |
| 49? | 74207281 | 22338618 | 44677235 | 2016 | Cooper, Woltman (prime95), Kurowski & Blosser (PrimeNet), GIMPS et al. |
(web page) |
| 50? | 77232917 | 23249425 | 46498850 | 2017 | Pace, Woltman (prime95), Kurowski & Blosser (PrimeNet), GIMPS et al. | (web page) |
| 51? | 82589933 | 24862048 | 49724095 | 2018 | Laroche, Woltman (prime95), Blosser (PrimeNet), GIMPS et al. | (web page) |
We put question marks instead of a number for the last of the Mersenne
primes because it will not be known if there are other Mersenne’s in between
these until a check and double check has been completed by GIMPS. See
the GIMPS Status Page for more information.
Not all smaller exponents have been tested.
Другие варианты реализации
В связи с изменениями в технологии, в частности, ростом производительности процессоров, были изобретены 64-битные и 128-битные версии МТ. 64-разрядная версия была предложена Такудзи Нисимурой в 2000 году, 128-разрядная − в 2006 году тоже Такудзи Нисимурой. Обе версии имеют тот же период, что и оригинальный MT.
64-битный MT имеет две версии. Первая версия использует то же рекурсивное соотношение, во вторую версию были добавлены ещё два вектора, что увеличило количество членов характеристического многочлена:
- xk+n:=xk+m2⊕xk+m1⊕xk+m⊕(xku∣xk+1l)A(2){\displaystyle x_{k+n}:=x_{k+m2}\oplus x_{k+m1}\oplus x_{k+m0}\oplus ({x_{k}}^{u}\mid {x_{k+1}}^{l})A\qquad (2)}
По сравнению с 32-разрядной MT, 64-разрядная версия работает быстрее. Все параметры для 64-битной версии приведены в таблице 2.
| ID | Для рекурсивного соотношения (1) | Для рекурсивного соотношения (2) | |||
|---|---|---|---|---|---|
| n | 312 | 312 | 312 | 312 | 312 |
| w | 64 | 64 | 64 | 64 | 64 |
| r | 31 | 31 | 31 | 31 | 31 |
| m | 156 | 156 | |||
| m | 63 | 63 | 63 | ||
| m1 | 151 | 151 | 151 | ||
| m2 | 224 | 224 | 224 | ||
| a | B5026F5AA96619E916 | F6A3F020F058B7A716 | B3815B624FC82E2F16 | 8EBD4AD46CB39A1E16 | CACB98F78EBCD4ED16 |
| b | D66B5EF5B4DA000016 | 28AAF6CDBDB4000016 | 599CFCBFCA66000016 | 656BEDFFD9A4000016 | A51DBEFFDA6C000016 |
| c | FDED6BE00000000016 | FDEDEAE00000000016 | FFFAAFFE0000000016 | FDFECE7E0000000016 | FFEE9BF60000000016 |
| u | 29 | 29 | 26 | 26 | 26 |
| s | 17 | 17 | 17 | 17 | 17 |
| t | 37 | 37 | 33 | 33 | 33 |
| l | 41 | 41 | 39 | 39 | 39 |
Наше время
Надо сказать, что победе над гипотезой Мерсенна способствовало появление так называемого теста Люка-Лемера. Суть его заключается в следующем: для фиксированного числа Мерсенна вычисляется некоторая рекуррентная последовательность. Рекуррентная формула для членов этой последовательности, во-первых, относительно проста, а во-вторых, для проверки требуется взять p — 2 члена последовательности, где p — нечетный простой показатель числа Мерсенна. Сложность работы алгоритма составляет порядка третьей степени log n, где n — само число Мерсенна. Использование разного рода методов быстрого умножения, как, например, метода Шёнхаге — Штрассена, позволяет немного ускорить работу, однако кардинально сложности не меняет.
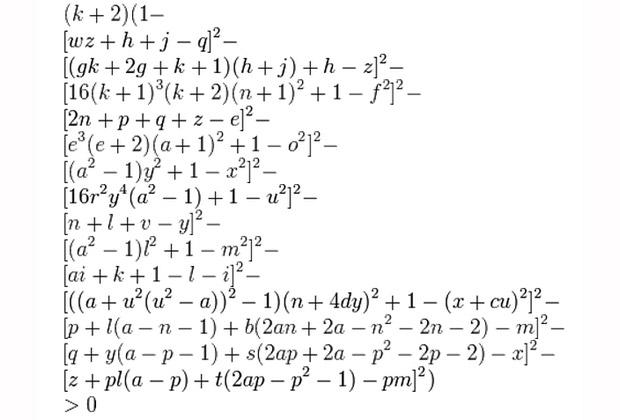
Многочлен Джонса
Формула для генерации простых чисел: множество неотрицательных значений этого многочлена от 26 переменных для всевозможных наборов из 26 натуральных чисел дает все простые числа.
Нужно понимать, что это крайне низкая вычислительная сложность, то есть алгоритм работает довольно быстро. Для сравнения, самый быстрый детерминистский алгоритм проверки простоты из существующих — тест Агравала-Каяла-Саксены c улучшениями Померанса-Ленстры — имеет сложность порядка (log n)6. Относительную простоту программирования и низкую вычислительную сложность теста Люка-Лемера ученые оценили только с появлением компьютеров.
В 60-е годы прошлого века интерес к числам Мерсенна стал спадать. Связано это было с тем, что перспективы вычислительной техники на тот момент виделись довольно туманными, а использование суперкомпьютеров для поиска больших простых чисел казалось довольно расточительным. В 1968 году в Университете Иллинойса было открыто 23-е простое число Мерсенна с показателем 11213. На тот момент это было настолько великим достижением, что Пол Бейтман, который руководил кафедрой теории чисел в этом университете, заказал специальную печать для корреспонденции, на которой, помимо даты, красовалась надпись «211213 — 1 — простое число».
Лэндон Нолл
Фото: JC Dill / Wikipedia
В 1970-х годах интерес к числам Мерсенна снова активизировался. Причиной тому стала история двух тогда еще американских школьников — Лауры Никел и Лэндона Нолла. Не особо разбираясь в математических тонкостях вопроса, они написали программу для проверки чисел Мерсенна на простоту с помощью теста Люка-Лемера и прогнали ее на суперкомпьютере в местном университете. В результате они смогли найти 25-е и 26-е простые числа Мерсенна с показателями 21 701 и 23 209 соответственно. Это были самые большие простые числа из известных на тот момент. Нолл после этого стал обладателем еще одного рекорда — в 1989 году он принял участие в открытии самого большого простого числа, которое не является числом Мерсенна (это так называемое простое число Амдала 6, названное так в честь рабочей группы, открывшей его, и равное 391581*2216193-1).
История с открытием школьников попала на телеэкраны, и поиск простых чисел Мерсенна снова вернулся в моду. Следующие успехи в этой деятельности были связаны с суперкомпьютерами Крэй — один из сотрудников компании-производителя Дэвид Словински написал программу для поиска простых чисел Мерсенна, работавшую на этих машинах, пока они не использовались. Наконец, современный облик этот процесс приобрел при помощи программиста Джорджа Уолтмана, в 1995 году создавшего проект распределенных вычислений GIMPS (Great Internet Mersenne Prime Search).
Проект, предназначенный для работы на i386, к концу первого года существования насчитывал уже более тысячи участников. Это был первый исследовательский проект распределенных вычислений в истории. Первое простое число Мерсенна (в настоящее время в рамках проекта открыто уже 14 штук) стало известно в 1996 году. Сейчас программу, работающую под всеми основными операционными системами, себе любой желающий. Суммарная вычислительная мощность проекта к концу 2012 года составляла уже 95 терафлопс.
Труды
Физико-математические сочинения:
Euclidis elementorum libri (Paris, 1626, комментарии к Евклиду).
Les Mécaniques de Galilée (Paris, 1634, перевод последнего труда Галилея).
Questions théologiques, physiques (1634).
L’Harmonie universelle (1636, содержательная теория музыки и музыкальных инструментов).
Nouvelles découvertes de Galilée (1639, открытия Галилея).
Cogitata physico-mathematica (Париж, 1644)
В этом сочинении обращают на себя внимание данные автором доказательства теорем о простых и о так называемых совершенных числах.
Novae observationes physico-mathematicae (3 тома, Париж, 1647).
Universae Geometriae mixtaeque Mathematicae synopsis (1664).. Философские и теологические сочинения Мерсенна:
Философские и теологические сочинения Мерсенна:
- Quaestiones celeberrimae in Genesim (1623, комментарии на Книгу Бытия).
- L’impiété des déistes et des plus subtils libertins découverte et réfutée par raisons de théologie et de philosophie» (1624).
- La vérité des sciences contre les sceptiques et les pyrrhoniens (1638).
Perfect Numbers and a Few Theorems
Many ancient cultures were concerned with the relationship of a number with the
sum of its divisors, often giving mystic interpretations. Here we are concerned
only with one such relationship:
For example, 6 is the first perfect number because 6=1+2+3. The next is 28=1+2+4+7+14.
The next two are 496 and 8128. These four were all known before the time of Christ.
Look at these numbers in the following partially factored form:
Do you notice they all have the same form 2n-1(2n-1)
(for n = 2, 3, 5, and 7 respectively)? And that in each case 2n-1 was a Mersenne prime? In fact it is easy to show the following theorems:
So the search for Mersennes is also the search for even perfect numbers!
You may have also noticed that the perfect numbers listed above (6, 28, 496,
8128) all end with either the digit 6 or the digit 8—this is also very easy
to prove (but no, they do not continue to alternate 6, 8, 6, 8,…). If
you like that digit pattern, look at the first four perfect numbers in binary:
(The binary digit pattern is a consequence of Theorem One.) It is whether or not there is an odd perfect number, but if there is one it is big! This is probably the oldest unsolved problem in all of mathematics.
When checking to see if a Mersenne number is prime, we usually first look for
any small divisors. The following theorem of Euler and Fermat is very
useful in this regard.
for some integer k .
Finally, we offer the following for your perusal:
Что такое простое число?
Оно действительно очень простое, потому что делится только на единицу и на самого себя. 2,3, 5,7 – это самые первые простые числа. Но дальше все начинает усложняться. Еще Эвклид в своих «Началах» доказал, что таких чисел бесконечное множество и самое большое найти просто нельзя.
Проблема в том, что большое простое число очень трудно найти. Список таких чисел веками расширялся методом проб и ошибок. Интерес к ним, то затухал, то разгорался вновь. Новый взрыв интереса произошел в 17 веке благодаря Марену Мерсенну, францисканскому монаху, теологу и математику, другу великого Рене Декарта. Как и многие математики той эпохи, он всю жизнь занимался поиском совершенных чисел, то есть таких чисел, которые представляют собой сумму всех своих делителей (самым маленьким совершенным числом является число 6=2+3+1). Однако однажды Мерсенн заинтересовался числами другого вида. Это были степени двойки, уменьшенные на единицу. Например, 2 в степени 1 — 1 = 1; 2 в степени 2 — 1 = 3, 2 в степени 3 – 1 = 7. Первые три числа, полученные по этой формуле, оказались простыми, но уже четвертое (2 в степени 4=15) было составным. Мерсенну стало любопытно, как распределяются простые и составные числа в этой последовательности.
В 1648 году Мерсенн выпустил загадочный труд Cogitata Physica-Mathematica. В этой работе, не особенно утруждая себя доказательствами, он предположил, что двойка в степенях 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257, уменьшенная на единицу, обязательно даст в результате простое число. Все остальные числа, рассчитанные по этой формуле, будут составными. Почему он так решил – непонятно. Мерсенн и сам не настаивал на своей гипотезе. Однако после его смерти она стала необычайно популярна. С тех пор простые числа такого вида стали называться числами Мерсенна, а его формула – популярной для определения новых больших простых чисел. Числа Мерсенна встречаются очень редко, и пока неизвестно, есть ли какая-то зависимость между номером числа Мерсенна и его величиной. Если такая зависимость есть, она заметно ускорит поиск новых больших простых чисел. Но главной загадкой по-прежнему остается вопрос, конечен ли ряд чисел Мерсенна.
Эпоха компьютерных технологий вернула интерес к поиску большого простого числа. Двое американских школьников – Лаура Никел и Лэндон Нолл — в конце 70-х обнаружили 25-е простое число Мерсенна, используя мощный по тем временам компьютер. Степень, в которую надо было возвести двойку, оказалась равна 21 701. На тот момент это было самое большое простое число. Впрочем, чуть позже Нолл уже в одиночку открыл и следующее, 26-е число. Успех школьников подтвердил, что в компьютерную эпоху добывать простые числа могут не только великие математики.
Исходная гипотеза Мерсенна
Исходная гипотеза, называемая гипотезой Мерсенна, это утверждение Марена Мерсенна в его работе Cogitata Physica-Mathematica (1644; см. Dickson 1919), что числа 2n−1{\displaystyle 2^{n}-1} простые для n = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 и 257 и составные для всех остальных положительных целых чисел n ≤ 257. Ввиду размеров этих чисел Мерсенн не проверил, и не мог проверить все эти числа в 17-м веке. В конечном счёте, после трёх столетий и доступности новых техник, таких как тест Люка — Лемера, было установлено, что гипотеза Мерсенна содержала пять ошибок, а именно, два составных (n = 67, 257) и три пропущенных простых (n = 61, 89, 107) чисел. Правильный список: n = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107 и 127.
Хотя исходная гипотеза Мерсенна не верна, она привела к Новой гипотезе Мерсенна.
Биография
Родился в крестьянской семье, в посёлке Уазе (фр. Oizé; ныне — в департаменте Сарта). Учился в иезуитском коллеже в Ла-Флеш, вместе с Декартом, тесную дружбу с которым Мерсенн пронёс через всю жизнь.
В 1611 году Мерсенн присоединился к францисканскому ордену «минимов». Далее он продолжил обучение в Париже. В 1613 году был рукоположен в священники, но не прекратил обучения, занявшись математикой, музыкой и философией. Совершил несколько путешествий по Европе, побывал в Италии, Германии, Голландии и других странах. Во время поездок приобретал новые знакомства, завязывал переписку, слушал лекции в местных университетах. Затем Мерсенн вернулся в Париж, поселился в монастыре и последующие десятилетия отдал науке и преподаванию философии.
Став до некоторой степени центральной фигурой, объединяющей учёных разных стран в области физико-математических наук, своей деятельностью Мерсенн выполнял, в ограниченных, конечно, размерах, функции не существовавшей ещё в его время Парижской Академии наук. В течение его продолжительного пребывания в Париже у него еженедельно происходили собрания математиков и физиков, с целью взаимного обмена идеями и мыслями, а также информирования о результатах предпринятых исследований (четверги Мерсенна). Позднее из этого кружка образовалась, при содействии Кольбера, Парижская академия наук (1666).
Умер в возрасте 60 лет (1648 год) от лёгочного абсцесса. Роль координатора после Мерсенна некоторое время, вплоть до создания в 1666 году Парижской академии, исполнял .
The Lucas-Lehmer Test and Recent History
Mersenne primes (and therefore even ) are
found using the following theorem:
(It is also possible to start with S(1)=10 and certain other values depending
on p.) In pseudo-code this test is:
The theory for this test was initiated by Lucas in the late 1870’s and then made into this simple test about 1930 by Lehmer. The sequence S(n) is computed modulo 2p-1 to save time.
This test is ideal for binary computers because the division by 2p-1
(in binary) can be done using rotation and addition only. (See the pages on proving primality for more information
of proving numbers are prime.)
In 1811 Peter
Barlow wrote in his text Theory of Numbers that 230(231-1)
«is the greatest that will be discovered; for as they are merely
curious, without being useful, it is not likely that any person will attempt
to find one beyond it.» I wonder what he would have made of the first
attempts to climb Mount Everest, to run faster miles, or to jump a longer broad
jump—other tasks that are curious but not useful. Obviously no one in
the late 1800’s had any idea of the power of modern computers. What might
we know about the machines of 50 years from now? (See also «Why
find big primes?»)
After the 23rd Mersenne prime was
found at the University of Illinois, the mathematics department was so proud
that the chair of their department, Dr. Bateman, had their postage meter changed
to stamp «211213-1 is prime» on each envelope. This was used
until the four color theorem was proved in 1976. (In 1985 Dr. Bateman printed
several copies of the earlier imprint—the image on the left is from one of
these.)
The 25th and 26th Mersenne primes were found by high-school students Laura
Nickel and Landon Curt Noll, who, though
they had little understanding of the mathematics involved, used Lucas’ simple
test on the local university’s mainframe (CSUH’s CDC 174) to find the next two
primes. Their discovery of the first prime made the national television
news and the front page of the New York times. They went their separate
ways after finding the first prime, but Noll kept the program running to find
the second—so Noll claims complete ownership. Noll searched later, and
though he never found another Mersenne prime, he is one of a team that holds
the record for the largest non-Mersenne prime. He currently works for
Silicon Graphics.
Slowinski, who works for Cray computers,
has written a version of the Lucas test that he has convinced many Cray labs
around the world to run in their spare time (time that would be lost otherwise).
He had to delay announcing one of his prime records until he got permission
to begin looking for it. Slowinski’s search for record primes is «not
so organized as you would suppose» (his words), as he does not search systematically.
In fact, looking at the table of Mersennes you see he missed the 29th prime
but found the 30th and 31st. Colquitt & Welsh worked to fill in the
gaps and found the 29th.
Enter George Woltman, an excellent
programmer and organizer. Starting in late 1995 he gathered up the disparate
databases and combined them into one. Then he placed this database, and a free,
highly optimized program for search for Mersennes onto the web. This began GIMPS (the Great Internet Mersenne
Prime Search) which: has now found the largest known Mersennes, has scanned
all of the regions left unexplored between the previous record primes, combines
the efforts of dozens of experts and thousands of
amateurs, and which offers free
software for most computer platforms.
In late 1997 Scott Kurowski (and
others) established PrimeNet to automate
the selection of ranges and reporting of results for GIMPS, now almost anyone
can join this search!
Свойства
Вихрь Мерсенна является витковым регистром сдвига с обобщённой отдачей (TGFSR) (англ. twisted generalised feedback shift register). «Вихрь» — это преобразование, которое обеспечивает равномерное распределение генерируемых псевдослучайных чисел в 623 измерениях (для линейных конгруэнтных генераторов оно ограничено 5 измерениями). Поэтому функция корреляции между двумя последовательностями выборок в выходной последовательности вихря Мерсенна пренебрежимо мала.
Псевдослучайная последовательность, порождаемая вихрем Мерсенна, имеет очень большой период, равный числу Мерсенна, что более чем достаточно для многих практических приложений.
Существуют эффективные реализации Вихря Мерсенна, превосходящие по скорости многие стандартные ГПСЧ (в частности, в 2—3 раза быстрее линейных конгруэнтных генераторов). Алгоритм вихря Мерсенна реализован в программной библиотеке Boost, Glib и стандартных библиотеках для C++, Python, Ruby, R, PHP, MATLAB, Autoit.
Выдаваемые вихрем Мерсенна последовательности псевдослучайных чисел успешно проходят статистические тесты DIEHARD, что подтверждает их хорошие статистические свойства.
Генератор не предназначен для получения криптографически стойких случайных последовательностей чисел. Для обеспечения криптостойкости выходную последовательность генератора необходимо подвергнуть обработке одним из криптографических алгоритмов хеширования.














