Что такое простые числа
Содержание:
- Кубические простые числа
- Миллиард = биллион?
- История использования нуля
- Абак
- Ноль в информатике и вычислительной технике
- Примечания
- Десять триллионов
- Ноль в языке и культуре
- Родина ноля — Индия
- 1 миллиард — это много?
- Числа
- Арабские цифры в Европе
- Свойства ноля
- Ноль или нуль: возможны оба варианта
- Ссылки
- Некоторые свойства простых чисел.
Кубические простые числа
Простые числа вида x3−y3x−y,x=y+1{\displaystyle {\frac {x^{3}-y^{3}}{x-y}},x=y+1}
7, 19, 37, 61, 127, 271, 331, 397, 547, 631, 919, 1657, 1801, 1951, 2269, 2437, 2791, 3169, 3571, 4219, 4447, 5167, 5419, 6211, 7057, 7351, 8269, 9241, 10267, 11719, 12097, 13267, 13669, 16651, 19441, 19927, 22447, 23497, 24571, 25117, 26227, 27361, 33391, 35317 (последовательность A002407 в OEIS).
а также x3−y3x−y,x=y+2{\displaystyle {\frac {x^{3}-y^{3}}{x-y}},x=y+2}
13, 109, 193, 433, 769, 1201, 1453, 2029, 3469, 3889, 4801, 10093, 12289, 13873, 18253, 20173, 21169, 22189, 28813, 37633, 43201, 47629, 60493, 63949, 65713, 69313, 73009, 76801, 84673, 106033, 108301, 112909, 115249
(последовательность A002648 в OEIS).
Миллиард = биллион?
Такое слово, как биллион, применяется для обозначения миллиарда только в тех государствах, в которых за основу принята «короткая шкала». Это такие страны, как Российская Федерация, Соединенное Королевство Великобритании и Северной Ирландии, США, Канада, Греция и Турция. В других странах понятие биллион означает число 1012 , то есть один и 12 нулей. В странах с «короткой шкалой», в том числе в России, эта цифра соответствует 1 триллиону.
Такая неразбериха появилась во Франции в то время, когда происходило становление такой науки, как алгебра. Изначально у миллиарда было 12 нулей. Однако все изменилось после появления основного пособия по арифметике (автор Траншан) в 1558 году), где миллиард — это уже число с 9 нулями (тысяча миллионов).
Несколько последующих столетий эти два понятия употреблялись наравне друг с другом. В середине 20 века, а именно в 1948 году, Франция перешла на длинную шкалу системы числовых наименований. В связи с этим, короткая шкала, некогда позаимствованная у французов, все же отличается от той, которой они пользуются сегодня.
Исторически сложилось так, что Соединенное Королевство использовало долгосрочный миллиард, но с 1974 года официальная статистика Великобритании использовала краткосрочную шкалу. С 1950-х годов краткосрочная шкала все чаще использовалась в области технической письменности и журналистики, несмотря на то, что по-прежнему сохранялась долгосрочная шкала.
История использования нуля
Впервые появился в Индии, где именовался санскритским словом «сунья» («пустота»; «отсутствие»), и широко использовался в поэзии и священных текстах. Через арабов, называвших его «сифр» (отсюда слова «цифра» и лат. zero, ноль), попал в Западную Европу.
Вавилонские математики использовали особый клинописный значок для шестидесятеричного нуля, начиная примерно с 300 г. до н. э., а их учителя-шумеры, вероятно, сделали это ещё раньше. Однако символ «двойной клин» вавилонских мудрецов никогда не означал «число 0». Хотя в их системе счисления 0 отсутствует, египетские математики уже со Среднего царства (начало II тысячелетия до н. э.) использовали для обозначения нуля иероглиф нфр («прекрасный»), также означавший начало отсчёта в схемах храмов, пирамид и гробниц.
Своеобразные коды нуля использовали ещё до нашей эры древние майя и их соседи в Центральной Америке (древние майя обозначали ноль стилизованным изображением ракушки).
В китайских цифрах для обозначения нуля пользуются знаком 〇 — одним из иероглифов императрицы У Цзэтянь.
В Древней Греции число 0 известно не было. В астрономических таблицах Клавдия Птолемея пустые клетки обозначались символом ο (буква омикрон, от др.-греч. οὐδέν — ничего); не исключено, что это обозначение повлияло на появление нуля, однако большинство историков признаёт, что десятичный нуль изобрели индийские математики. Без нуля была бы невозможна изобретённая в Индии десятичная позиционная запись чисел. Первый код нуля обнаружен в индийской записи от 876 г. н. э., он имеет вид привычного нам кружочка.
В Европе долгое время 0 считался условным символом и не признавался числом; даже в XVII веке Валлис писал: «Нуль не есть число». В арифметических трудах отрицательное число истолковывалось как долг, а ноль — как ситуация полного разорения. Полному уравниванию его в правах с другими числами особенно способствовали труды Леонарда Эйлера.
Исследования показали, что манускрипт Бакхшали содержит, вероятно, самое древнее упоминание ноля.
Абак
Счётная доска, состоящая из углублений, соответствующих определенным разрядам, в которые укладываются камешки или бусины, знакома культурам разных народов и эпох. Известны и другие разновидности абака – веревки с узелками или шнуры с бусинами. Следующей ступению в развития такого приспособления стали счеты, применявшиеся до появления калькуляторов.
История числа ноль – это процесс возникновения математического понятия и начало применения символа, его обозначающего. И абак, и счёты являются в некотором смысле и средством визуализации числового ряда. Пустое место в соответствующем углублении или отсутствующая костяшка на счетах делала абстрактное понятие нуля наглядным. Символ, обозначающий его, впервые появился у математиков и астрономов Древнего Вавилона.

Ноль в информатике и вычислительной технике
Подавляющее большинство компьютеров опираются на двоичную систему, то есть их память содержит только нули и единицы. Нечисловые данные используют стандартную кодировку — например, логические понятия ИСТИНА и ЛОЖЬ обычно кодируются как 1 и 0 соответственно, а для текстовых данных разных языков разработана универсальная кодировка Юникод..
В компьютерах существует понятие «машинного нуля» — это число с плавающей запятой и таким отрицательным порядком, которое воспринимается компьютером как ноль.
Ещё одна особенность представления данных в информатике: во многих языках программирования элементы массива данных нумеруются не с привычной единицы, а с нуля, так что описание real M(n) означает .массив M,M1…Mn−1.{\displaystyle M_{0},M_{1}\dots M_{n-1}.} Платформа Microsoft .NET Framework закрепила этот стандарт и даже перевела на него Visual Basic, который изначально использовал нумерацию с единицы.
В SQL-базах данных поле может иметь специальное значение NULL, которое означает не ноль, а неопределённое значение. Любое выражение, в котором участвует NULL, дает в результате NULL.
В математике −=+={\displaystyle -0=+0=0}; то есть −,+{\displaystyle -0,+0} представляют одно и то же число, не существуют отдельные положительный и отрицательный нули. Однако в некоторых компьютерных форматах (например, в стандарте IEEE 754 или в прямом и обратном коде) для нуля имеются два различных представления: положительное (с положительным знаком) и отрицательное; см. подробнее −0 (программирование). На результаты вычислений, впрочем, эти различия не влияют.
| Десятичноепредставление | Двоичное представление (8 бит) | ||
|---|---|---|---|
| прямой | обратный | дополнительный | |
| +0 | 0000 0000 | 0000 0000 | 0000 0000 |
| -0 | 1000 0000 | 1111 1111 |
 Пометки нулей, чтобы не путать их с буквой О
Пометки нулей, чтобы не путать их с буквой О
При работе с компьютером из-за опасности спутать цифру с латинской или русской буквой О, что может вызвать серьёзные последствия, одно время действовала рекомендация, : {\displaystyle {\cancel {0}}}. Иногда поступали наоборот: при программировании на ЭВМ «Минск-32» перечёркивали букву О, а не нуль. В начале эпохи персональных компьютеров в текстовом режиме работы дисплея и на многих матричных принтерах нуль также выводился в перечёркнутом виде (некоторые принтеры имели встроенные переключатели для включения и отключения режима перечёркивания нуля). На дисплеях IBM 3270 цифра 0 изображалась с точкой в центре. В современных компьютерных шрифтах буква О заметно шире нуля, так что перечёркивание обычно не требуется. Перечёркнутый ноль не имеет отдельного символа Юникода, но может быть получен как символ U + 0030, сразу за которым идёт U + FE00.
Примечания
- ↑
- .
- Нуль // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. — С. 1082.
- Нуль // Большой Энциклопедический словарь (рус.). — 2000. // Большой Энциклопедический словарь. 2000.
- Большой толковый словарь русского языка. Гл. ред. С. А. Кузнецов. Первое издание: СПб.: Норинт, 1998.
- ↑ Потапов М. К., Александров В. В., Пасиченко П. И. Алгебра и анализ элементарных функций. — М.: Наука, 1981. — С. 9. — 560 с.
- . NCSU COE People. Дата обращения 12 августа 2019.
- ↑ Савин А. П. Энциклопедический словарь юного математика / сост. А. П. Савин. — М.: «Педагогика», 1989. — С. 219.
- Брич З. С., Воюш В. И., Дегтярёва Г. С., Ковалевич Э. В. Программирование на языке Ассемблера ЕС ЭВМ. — М.: Статистика, 1976. — 296 с. — С. 13—14, 19.
- Кулаковская В. П., Романовская Л. М., Савченко Т. А., Фельдман Л. С. Кобол ЭВМ Минск-32. Пособие для работников вычислительных центров. — М.: Статистика, 1973. — 284 с.
- Брябрин В. М. Программное обеспечение персональных ЭВМ. 3-е изд. — М.: Наука, 1990. — 272 с. — ISBN 5-02-014824-5. — С. 17, 113—114.
- Смирнов Н. Н. Программные средства персональных ЭВМ. — Л.: Машиностроение, 1990. — 272 с. — ISBN 5-217-00029-5. — С. 13, 80—81.
- Ламберто Гарсия дель Сид. Особые числа других культур → 116 // Замечательные числа. Ноль, 666 и другие бестии. — DeAgostini, 2014. — Т. 21. — С. 116. — 159 с. — (Мир математики). — ISBN 978-5-9774-0716-8.
- .
- (англ.). The Guardian (14 September 2017). Дата обращения 19 сентября 2017.
- Ламберто Гарсия дель Сид. Особые числа других культур → 116 // Замечательные числа. Ноль, 666 и другие бестии. — DeAgostini, 2014. — Т. 21. — С. 115. — 159 с. — (Мир математики). — ISBN 978-5-9774-0716-8.
- «Zentralblatt für Mathematik», апрель, 1957, сообщение чешского историка математики Г. Феттера.
- Депман И. Я. История Арифметики. — изд. «Просвещение», Москва, 1965, стр. 89.
- Депман И. Я. История Арифметики. — изд. «Просвещение», Москва, 1965, стр.90
- Joseph, George Gheverghese. The Crest of the Peacock: Non-European Roots of Mathematics (Third Edition) (англ.). — Princeton University Press, 2011. — P. 86. — ISBN 978-0-691-13526-7.
Десять триллионов
| Сумма цифр | |
| Произведение цифр | |
| Произведение цифр (без учета ноля) | |
| Количество цифр в числе | (четырнадцатизначное число) |
| Все делители числа | 1, 2, 4, 5, 8, 10, 16, 20, 25, 32, 40, 50, 64, 80, 100, 125, 128, 160, 200, 250, 256, 320, 400, 500, 512, 625, 640, 800, 1000, 1024, 1250, 1280, 1600, 2000, 2048, 2500, 2560, 3125, 3200, 4000, 4096, 5000, 5120, 6250, 6400, 8000, 8192, 10000, 10240, 12500, 12800, 15625, 16000, 20000, 20480, 25000, 25600, 31250, 32000, 40000, 40960, 50000, 51200, 62500, 64000, 78125, 80000, 100000, 102400, 125000, 128000, 156250, 160000, 200000, 204800, 250000, 256000, 312500, 320000, 390625, 400000, 500000, 512000, 625000, 640000, 781250, 800000, 1000000, 1024000, 1250000, 1280000, 1562500, 1600000, 1953125, 2000000, 2500000, 2560000, 3125000, 3200000, 3906250, 4000000, 5000000, 5120000, 6250000, 6400000, 7812500, 8000000, 9765625, 10000000, 12500000, 12800000, 15625000, 16000000, 19531250, 20000000, 25000000, 25600000, 31250000, 32000000, 39062500, 40000000, 48828125, 50000000, 62500000, 64000000, 78125000, 80000000, 97656250, 100000000, 125000000, 128000000, 156250000, 160000000, 195312500, 200000000, 244140625, 250000000, 312500000, 320000000, 390625000, 400000000, 488281250, 500000000, 625000000, 640000000, 781250000, 800000000, 976562500, 1000000000, 1220703125, 1250000000, 1562500000, 1600000000, 1953125000, 2000000000, 2441406250, 2500000000, 3125000000, 3200000000, 3906250000, 4000000000, 4882812500, 5000000000, 6250000000, 7812500000, 8000000000, 9765625000, 10000000000, 12500000000, 15625000000, 16000000000, 19531250000, 20000000000, 25000000000, 31250000000, 39062500000, 40000000000, 50000000000, 62500000000, 78125000000, 80000000000, 100000000000, 125000000000, 156250000000, 200000000000, 250000000000, 312500000000, 400000000000, 500000000000, 625000000000, 1000000000000, 1250000000000, 2000000000000, 2500000000000, 5000000000000, 10000000000000 |
| Наибольший делитель из ряда степеней двойки | |
| Количество делителей | |
| Сумма делителей | |
| Простое число? | Нет |
|
Полупростое число? |
Нет |
| Обратное число | 1e-13 |
| Индо-арабское написание | ١٠٠٠٠٠٠٠٠٠٠٠٠٠ |
| Азбука морзе | .—- —— —— —— —— —— —— —— —— —— —— —— —— —— |
|
Факторизация |
* * * * * * * * * * * * * * * * * * * * * * * * * |
| Двоичный вид | 10010001100001001110011100101010000000000000 |
| Троичный вид | 1022101222202012020020211101 |
| Восьмеричный вид | 221411634520000 |
| Шестнадцатеричный вид (HEX) | 9184E72A000 |
| Перевод из байтов | терабайтов гигабайтов мегабайт килобайтов 0 байтов |
| Наибольшая цифра в числе(возможное основание) | (2, двоичный вид) |
| Перевод двоичной записи в десятичную | |
| Число Фибоначчи? | Нет |
|
Нумерологическое значение |
мужество, логика, независимость, самостоятельность, индивидуализм, смелость, решительность, изобретательность |
| Синус числа | -0.2888852948175251 |
| Косинус числа | 0.95736371690084 |
| Тангенс числа | -0.3017508285698347 |
| Натуральный логарифм | 29.933606208922594 |
| Десятичный логарифм | |
| Квадратный корень | 3162277.6601683795 |
| Кубический корень | 21544.346900318826 |
| Квадрат числа | 1e+26 |
| Перевод из секунд | неделя дня часов минут секунд |
| MD5 | 7b00c4611cac79cdb3913a03ca5423b9 |
| SHA1 | de5255cb1537be30b97ea32a723025033a0fda40 |
| Base64 | MTAwMDAwMDAwMDAwMDA= |
| QR-код числа 10000000000000 |
Ноль в языке и культуре
- «Мы почитаем всех нулями, а единицами — себя» — цитата из поэмы Пушкина «Евгений Онегин» (глава 2, строфа 14), употребляется иронически, когда говорят о чьем-либо завышенном самомнении и пренебрежительном отношении к окружающим.
- На нуле — отсутствие чего-либо. Например, «финансы на нуле» (разговорное употребление).
- Ноль в переносном значении означает ничтожного, незначительного человека, например: «Он абсолютный ноль».
- Выражение ноль без палочки, когда идёт речь о человеке, означает, что он не имеет никакого влияния, значения (разговорное и шутливое употребление), а также некомпетентного, глупого человека.
- Ноль внимания — отсутствие внимания.
- Выражение ноль-ноль, употребляемое после указания часа суток, означает: ровно в таком-то часу, без минут. В спорте это же выражение может обозначать ничейный исход игры, состязания.
- С нуля начинать — начинать на пустом месте (разговорное употребление) или приступать к чему-либо без предварительной подготовки.
- Стричь под ноль — то же, что стричь наголо.
Родина ноля — Индия
Что же изобрели индийские математики? Махавира (850 г.), Брахмагупта (1114 г.), Ариабхата (476 г.) — авторы трактатов, в которых во многом оформилась современная система записи чисел и правила основных арифметических операций. Историки считают, что десятичность системы счисления была заимствована индийцами у китайцев, а позиционный характер её – у вавилонян. Есть мнение, что символ нуля был также заимствован индийцами из работ Птолемея.
Первым из математиков, сформулировавшим законченную числовую систему, которая остается до сих пор в неизменном виде и служит большей части человечества, был Хорезми Мухаммед бен Муса (787-850), живший в Багдаде. В его «Книге об индийском счете» подробно описаны девять арабских цифр и дан ответ на вопрос: «Является ли 0 числом?» Упоминание нуля в этой книге считается первым. Латинский перевод этого труда, стал широко известен в Европе в XII веке и положил начало распространению восточных математических знаний.
В отличие от европейцев, вечность у восточных философов вызывала благоговение. Поэтому ноль в уравнениях древнеиндийских ученых окончательно стал не только символом отсутствия единиц в соответствующем разряде, но и натуральным числом, влияющим на результат вычислений. Прибавление ноля, умножение на 0 – всё это обрело значение осмысленных математических операций.
Само написание цифр от 1 до 0 обрело окончательный вид тоже благодаря древнеиндийским математическим трактатам, и те символы, что в Европе принято называть арабскими, сами арабы называют индийскими.
История числа «ноль» нашла отражение в этимологии основных математических терминов. Слово «цифра» имеет арабские корни и происходит от слова «аль-сифр», что означает «пустой, нуль». Английское «зеро» отдаленно напоминает «зефир» — ветер с востока, — именно с Востока в Европу пришла окончательно оформленная, рациональная и удобная числовая система.
1 миллиард — это много?
Существуют две шкалы измерения — короткая и длинная. Во всем мире в области науки и финансов 1 миллиард составляет 1 000 миллионов. Это по короткой шкале. По ней это число с 9 нулями.
Существует также длинная шкала, которая используется в некоторых европейских странах, в том числе во Франции, и раньше использовалась в Великобритании (до 1971 года), где миллиард составлял 1 миллион миллионов, то есть единица и 12 нулей. Эту градацию еще называют долгосрочным масштабом. Короткая шкала теперь является преобладающей при решении финансовых и научных вопросов.
Некоторые европейские языки, такие как шведский, датский, португальский, испанский, итальянский, голландский, норвежский, польский, немецкий, используют миллиард (или биллион) имеенно в этой системе. В русском языке число с 9 нулями также описывается для короткой шкалы тысяча миллионов, а триллион — это миллион миллионов. Это позволяет избежать лишней путаницы.
Числа
| i | 2i | 3i | Такими числами Стив Джобс считает яблоки | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10−42 | 10−42+i | 10−42+2i | 10−42+3i | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1+i | 1+2i | 1+3i | Возможно, равно соответственно 0,i,2i,3i (см. 1=0) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2+i | 2(1+i) | 2+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3+i | 3+2i | 3(1+i) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| π | π+i | π+2i | π+3i | π+πi | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4+i | 4+2i | 4+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5+i | 5+2i | 5+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5+i | 5+2i | 5+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6+i | 6+2i | 6+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| VI | VI+I·i | VI+II·i | VI+III·i | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7+i | 7+2i | 7+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8+i | 2(4+i) | 8+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9+i | 9+2i | 3(3+i) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10+i | 2(5+i) | 10+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| !11 | !11+i | !11+2i | !11+3i | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12+i | 6(2+i) | 3(4+i) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13+i | 13+2i | 13+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . | . | . | . | Пропуск на месте чисел, которые автору были неинтересны или которые он забыл | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| XVII | XVII+I*i | XVII+II*i | XVII+III*i | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . | . | . | . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 29+i | 29+2i | 29+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . | . | . | . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 с чем-то | 37 с чем-то+i | 37 с чем-то+2i | 37 с чем-то+3i | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . | . | . | . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42+i | 2(21+i) | 3(14+i) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43+i | 43+2i | 43+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45+i | 45+2i | 45+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . | . | . | . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 73+i | 73+2i | 73+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . | . | . | . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 403+i | 403+2i | 403+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 404+i | 404+2i | 404+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 407+i | 407+2i | 407+3i | Два числа, стоящие перед данным, запрещено указывать в нашем списке в связи с государственной тайной Непала. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . | . | . | . | Число пропущено по требованию правообладателя. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . | . | . | . | — | . | . | . | . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 502+i | 502+2i | 502+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . | . | . | . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 666+666i | 666+666i | 666+666i | С этого места числа идут без пропусков. Теорема Сотонского утверждает, что других чисел нет. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1011+1i | 1011+10i | 1011+11i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1234i | 1234j | 1234k | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1954 г. | 1954 гг. | 1954 ггг. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1984 | 1984 | 1984 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2032+i | 2032+2i | 2032+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5678i | 5678j | 5678k | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9000 | 9000 | 9000 | Дальше — больше. Больше 9000. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ABBAI | ABBAII | ABBAIII | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 100500+i | 100500+i+i | 100500+i+i+i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1000000+i | 1000000+2i | 1000000+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16777216+i | 16777216+2i | 16777216+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1000000000+i | 1000000000+2i | 1000000000+3i | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Ещё раз: 54 308 428 790 203 478 762 340 052 723 346 983 453 487 023 489 987 231 275 412 390 872 348 475 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . | . | . | . | Да, это — ещё один пропуск. А никто и не говорил, что будет легко. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ∞ | ∞ | ∞ | ∞ |
Арабские цифры в Европе
Одним из главных европейских пропагандистов арабской цифровой системы стал знаменитый итальянский математик Леонардо Фибоначчи. Его труд «Книга абака» (1202) познакомил европейских ученых с символами и правилами, с помощью которых арабы записывают математические операции. Первыми удобство и рациональность восточной математической модели оценили те, кто привык к ежедневному обращению с числами, – банкиры и торговцы. Они быстро переняли от арабских купцов систему счисления и написание цифр. Но в научную практику Европы эти знания плотно вошли только через 4 века, сменив принятую европейскими математиками античную систему.
Важное значение ноль обрел с введением в научный обиход прямоугольной системы координат, предложенной в XVII веке Рене Декартом. Ноль, расположенный в центре, приобрел значение зримой и визуально понятной точки отсчета трех осей координат
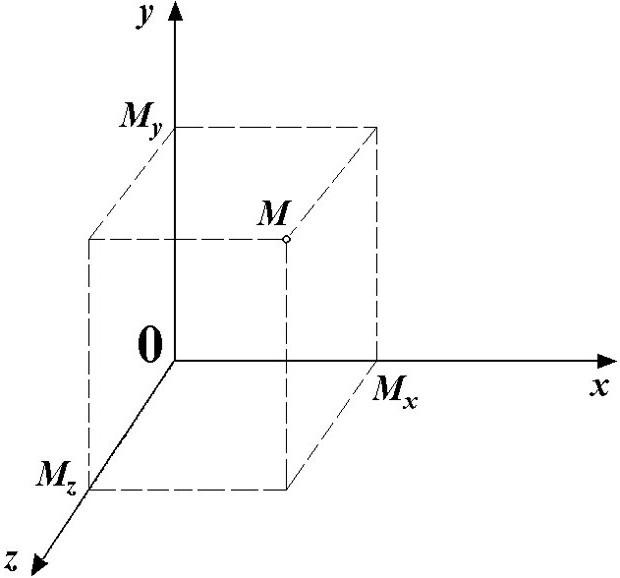
В России ноль вводился в практику стараниями Леонтия Магницкого, автора знаменитого учебника «Арифметика, сиречь наука числительная» (1703).
Свойства ноля
Ноль, который разграничивает положительные и отрицательные числа, обладает уникальными математическими свойствами. Это четное, не имеющее знака натуральное целое число. Сложение с нулем и вычитание нуля никак не влияет на число, а умножение на 0 даёт ноль. Деление на ноль считается не имеющей смысла операцией, которое в случае выполнения в компьютерной программе может нанести системе существенный вред.
Именно в попытке деления на 0 оказался смысл сбоя в компьютерной системе крейсера ВМФ США «Йорктаун», который произошел осенью 1997 года и привел к несанкционированному выключению двигательной установки. Некоректное отношение к числу, означающему «ничто», превратило мощный военный корабль в беспомощную неподвижную цель.
Значение этого числа существенно возрастало с развитием науки. Нуль возникает в областях не только чисто математических. Порог слышимости в акустике принимается за 0. Какое число стоит в начале шкалы многих измерительных приборов, известно и школьнику: 0 на шкале Цельсия – точка замерзания воды, начало отсчета долготы – нулевой меридиан и т. д.
Бинарное счисление, послужившее основой для создания современных вычислительных устройств, является позиционной системой счисления с основанием два. Это означает, что все данные, вводимые в компьютерные системы, кодируются сочетанием двух символов – единицы и нуля.

Роль компьютеров в современном мире становится определяющей для всех сторон жизни, а значит, история числа ноль, без которого их появление было бы невозможно, продолжается.
Ноль или нуль: возможны оба варианта
Теперь мы знаем, что правильность выбора «ноль» или «нуль» зависит от контекста фразы и от эпохи. Если вы пишете исторический роман, логично будет использовать «нуль», если речь идет о математическом примере — «ноль». Возможно, однажды «нуль» покинет русский язык, как и многие слова, которые устарели и ушли из языка за ненадобностью.
Какое из этих слов «важнее» в языке — неправильная постановка вопроса. Они совершенно равноправны и пока оба употребляются в тех или иных ситуациях. В свободном употреблении, в обычной разговорной речи, ошибиться не так страшно. Кроме того, иногда это придает фразе экспрессии и окрашивает нужными эмоциями.
Ссылки
- Скачать выпуски телеигры «Десять миллионов»
The Money Drop
|
«100 Milionë» (Албания) | |
Некоторые свойства простых чисел.
Допустим, p — простое, и p делит ab, тогда p делит a либо b.
Кольцо вычетов Znбудет называться полем только в случае, если n — простое.
Характеристика всех полей — это нуль либо простое число.
Когда p — простое, а a — натуральное, значит, ap-a можно поделить на p (малая теорема Ферма).
Когда G — конечная группа, у которой порядок |G| делят на p, значит, у G есть элемент порядка p (теорема Коши).
Когда G — конечная группа, и pn — самая высокая степень p, делящая |G|, значит, у G есть подгруппа порядка pn, которая называется силовская подгруппа, кроме того, число силовских подгрупп соответствует pk+1 для некоего целого k (теоремы Силова).
Натуральное p > 1 будет простым лишь в случае, если (p-1)! + 1 можно подулить на p (теорема Вильсона).
Когда n > 1 — натуральное, значит, есть простое p: n < p < 2 n (постулат Бертрана).
Ряд чисел, которые обратны к простым, расходится. Кроме того, при .
Всякая арифметическая прогрессия типа a, a + q, a + 2 q, a + 3 q, … , где a, q > 1 — целые взаимно простые числа, содержит нескончаемое число простых чисел (Теорема Дирихле о простых числах в арифметической прогрессии).
Любое простое число, которое большее тройки, можно представить как 6k+1 либо 6k-1, где k — натуральное число. Исходя из этого, когда разность нескольких последовательных простых чисел (при k>1) одинаковая, значит, она точно делится на шесть — к примеру: 251-257-263-269; 199-211-223; 20183-20201-20219.
Когда p > 3 — простое число, значит, p2-1 делится на 24 (работает и на нечётных чисел, которые не делятся на три).
Теорема Грина-Тао. Есть бесконечные арифметические прогрессии, которые состоят из простых чисел.
Ни одно простое число нельзя представить как nk-1, где n>2, k>1. Другими словами, число, которое следует за простым, не может быть квадратом либо более высокой степенью с основанием, которое больше двух. Можно сделать вывод, что когда простое число представлено как 2k-1, значит k — простое.
Ни одно простое число нельзя представить как n2k+1+1, где n>1, k>0. Другими словами, число, которое предшествует простому, не может быть кубом либо более высокой нечётной степенью с основанием, которое больше единицы.
Есть многочлены, у которых множество неотрицательных значений при положительных значениях переменных совпадает с множеством простых чисел. Пример:
Этот многочлен содержит 26 переменных, имеет 25. Самая низкая степень для известных многочленов представленного вида — пять при 42 переменных; самое маленькое количество переменных — десять при степени приблизительно 1,6·1045.















