Задача

Почему инструкция лучше решебника

В этой инструкции вы сможете найти типовые задачи, которые встречаются в курсах математики за 5 класс и разобранное, подробное, пошаговое решение. Это значительно полезнее книг, так как в них собраны далеко не все задачи, а те решения, которые есть, сжаты до минимума. Поэтому пользоваться решебником — порой не самый лучший выход.

Решебник по математике не всегда может дать исчерпывающую информацию

Как правило, при составлении ответов на свои задачи авторы не расписывают подробности и дают решения не ко всем номерам. Возможно, в расчёт идёт тот факт, что ученик способен справиться самостоятельно. Но вдруг ребёнок пропустил тему, что же тогда делать?

Лучший вариант — посмотреть решение типовых задач с пояснениями каждого действия. В этой инструкции собраны самые распространённые примеры, которые вызывают трудности у детей при решении, а также родителей при попытке объяснить задачу.

Подписи к слайдам:

Слайд 2

развитие умений и навыков применять математику для решения жизненных проблем, формирования умения учиться, самостоятельно приобретать знания

Слайд 3

Показать значимость математических задач на уроках и на практике Научиться решать задачи практического содержания Показать межпредметную связь

Слайд 4

Где применяется математика?

Слайд 5

1 этап. Перевод задачи на язык математики (построение математической модели). 2 этап. Решение математической задачи. 3 этап. Осмысление полученного решения, его применение для решения исходной задачи.

Слайд 6

Задача 1. Необходимо закупить кафельную плитку размерами 20 см u 20 см для покрытия пола ванной комнаты длиной 2 м 20 см и шириной 1 м 60 см. Сколько упаковок кафеля нужно купить, если в упаковке 10 штук плиток?

Слайд 7

Этап 1. Перевод задачи на язык математики Пол комнаты заменяем прямоугольником со сторонами 2 м 20 см и 1 м 60 см 1 м= 100 см 2 м 20 см=220 см и 1м60 см=160 см математической моделью кафельной плитки будет квадрат с длиной стороны 20 см.

Слайд 8

Покрытие пола плитками заменим покрытием прямоугольника квадратами Каким наименьшим количеством квадратов с длиной стороны 20 см можно полностью покрыть прямоугольник с длинами сторон 220 см и 160 см?

Слайд 9

Этап 2. Решение математической задачи 220: 20=11 – количество плиток в длину 160:20=8- количество плиток в ширину 3) 11*8=88 –необходимое количество плиток

Слайд 10

Этап 3. Осмысление полученного решения Нужно найти количество упаковок кафеля. В упаковке 10 плиток. Для покрытия пола требуется 88 плиток. Так как при делении на 10 числа 88 в частном получается 8 и в остатке 8, то число упаковок равно 8 + 1 = 9

Слайд 11

Проверь себя: 1. Сколько квадратных плиток размерами 10 смu10 см потребуется для того, чтобы покрыть прямоугольный участок стены размерами 1 м u 2 м? А. 200. Б. 20. В. 100. Г. 2 000. 2. Сколько квадратных плиток размерами 10 см u10 см потребуется для того, чтобы покрыть прямоугольный участок стены размерами 1 м 15 см u2 м? А. 230. Б. 240. В. 2 000. Г. 2 200

Слайд 12

Реши сам 1 . Облицовку стены прямоугольной формы длиной 3 м 50 см и высотой 2 м 55 см кафельными плитками начинают снизу. а) Сколько плиток размерами 15 см u 15 см понадобится для укладки одного горизонтального ряда плиток? б) Сколько понадобится уложить горизонтальных рядов? в) Сколько понадобится упаковок плиток, если в упаковке 10 плиток ?

Слайд 13

Итоги: Чтобы решить задачу, нужно: сначала проанализировать её условия и вытекающие из них следствия; уяснить требования задачи; попытаться найти путь к выполнению требований задачи

Задачи, решаемые алгебраическим способом

Пример 1

Из цистерны отлили 80 литров молока, в нем осталось на 240 литров больше, чем отлили. Сколько литров молока было в цистерне с самого начала?

Решение

• Начинаем с составления краткого условия в виде таблицы. В подобных типовых задачах нужно обозначать неизвестное за «x»;
• Потребуются три строки: сколько молока было, сколько его отлили и сколько осталось;
• Заполняем числами таблицу;

Таблица 7 — краткое условие задачи

Было	Х
Отлили	80
Осталось	240+80

• Приступаем к расчётам. Нам нужно узнать, сколько было молока изначально. Для этого составляем уравнение. От начального количества вычитаем отлитое и получаем остаток;
• Математически получаем такую запись: x-80=240+80;
• Начинаем решение с того, что считаем всё, что можно посчитать. В данном случае складываем правую часть уравнения. 240+80=320. Теперь уравнение имеет вид: x-80=320;
• Теперь находим «x». Используем базовое правило математики и получаем следующее: x=320+80. Считаем правую часть и получаем: x=400;
• Возвращаемся к началу и смотрим, что мы обозначили за «x». В этом примере за икс мы взяли объём молока, который был изначально. То есть, изначально было 400 литров молока;
• Записываем полученное значение в ответ.

Пример 2

Первое слагаемое на 52 больше второго слагаемого, а второе слагаемое на 14 меньше третьего слагаемого. Сумма трех слагаемых равна 327. Найдите каждое слагаемое.

• Записываем краткое условие в виде таблицы;
• Потребуется четыре строки, так как нам дали три слагаемых и их сумму;
• Заполняем таблицу числами, обозначив за икс последнее слагаемое. Выбираем третье, потому что от него зависят все остальные;

Таблица 8 — краткое условие задачи

1 слагаемое	(x-14)+52
2 слагаемое	x-14
3 слагаемое	x
Сумма	327

• Приступаем к расчётам. Для нахождения слагаемых нужно решить уравнение, после чего число подставить в выражения из таблицы.
• Уравнение составляется исходя из условия – три слагаемых и сумма – складываем значения из второго столбца таблицы и приравниваем это к сумме.
• Получится такое выражение: (x-14)+52+(x-14)+x=327.
• Открываем скобки и упрощаем выражение: 3x+24=327.
• Переносим числа в правую часть: 3x=303
• Считаем икс: 303:3=101.
• Теперь подставляем число 101 в таблицу вместо икса.
• Получается третье слагаемое равно 101; второе: 101-14=87; первое: 87+52=139.
• Эти числа записываем в ответ. Легко проверить правильность решения просто сложив эти значения. Если пример получается правильный, то и решено всё верно.

Для правильного решения этих типовых задач необходимо ничего не напутать с иксом. Лучше потратить больше времени и сразу всё проверить, чем переделывать задание сначала. Неправильное обозначение повлечёт за собой ошибку на протяжении всего решения

Популярное

Математика
26 августа 2019

Найди закономерность

Закономерность — это регулярные устойчивые взаимосвязи в количествах, свойствах и явлениях объектов. В математической закономерности нужно найти алгоритм, согласно которому в цепочке чисел происходит их повторение, изменение или замещение в соответствии с установленным правилом.

Любовь к учебе
6 сентября 2019

Как решать ребусы?

Разгадывание ребусов – отличное времяпровождение для любителей всевозможных головоломок и загадок. Это захватывающий процесс, суть которого заключается в том, чтобы расшифровать слово, фразу или предложение с помощью картинок и символов-подсказок: цифр, букв, запятых и прочих знаков.

Навыки
15 декабря 2019

15 сложных загадок на логику.

Логическая загадка любой сложности заставит вас подумать о давно забытых предметах, вспомнить содержание детских сказок и смириться с тем, что ваш ребенок находит ответы быстрее вас. Хотите проверить? Мы подготовили специальную подборку сложных логических загадок!

Более сложный уровень

Как научиться решать задачи по математике, используя таблицы? Все очень просто! Как правило, таблицы используются для упрощения и систематизации условия. Чтобы понять суть данного метода, разберем пример.

Перед вами книжный шкаф с двумя полками, на первой книг в три раза больше, чем на второй. Если с первой полки убрать восемь книг, а на вторую поставить 32, то их станет поровну. Ответьте на вопрос: сколько книг было первоначально на каждой полке?

Как научиться решать текстовые задачи по математике, сейчас все наглядно покажем. Для упрощения восприятия условия составим таблицу.

Условие

	1 полка	2 полка
Было	3х	х
Стало	3х-8	х+32

Теперь можем составить уравнение:

3х-8=х+32;

3х-х=32+8;

2х=40;

х=20 (книг) — было на второй полке;

20*3=60 (книг) — было на первой полке.

Ответ:60;20.

Вот наглядный пример решения задачи на составление уравнения с использованием вспомогательной таблицы. Она значительно упрощает восприятие.

Используем аналогии

Нас окружает неисчислимое множество крылатых выражений и метафор, которые проверены многими сотнями лет. Что же нам мешает взять их на вооружение? Ответ вас поразит: только наша природная лень! Давайте задумаемся: а откуда все остальные черпают новаторские идеи? Да просто из многовековой мудрости! Для этого и передаются из поколения в поколение притчи, чтобы подсказывать правильные выводы из повторяющихся ситуаций.

Все аналогии, которые содержат притчи, метафоры и наши собственные фантазии, условно можно разделить на четыре группы:

• Аналогии личностные. Чтобы понять суть какого-то явления, нужно представить себя его частью и постараться максимально в него вжиться. Выберите для этого трудно решаемую задачу по вашему профилю и подумайте, как ее решили бы именно вы – только так и возникают самые смелые и инновационные идеи, которые потом правят миром. Не исключено, что вы (и только вы) вполне сможете уловить ту суть, над которой бьются уже который год самые лучшие умы мира. Дерзайте – и весь мир будет у ваших ног!
• Аналогии прямые. Сопоставьте ежедневно решаемые вами задачи с задачами из других близких вам сфер. Никогда над этим не задумывались? А зря! Очень часто достаточно провести аналогии с другими видами работы – оказаться инноватором, предложившим более оптимальные пути решения самых сложных, как казалось раньше задач!
• Аналогии символические. Здесь вам нужно будет включить полет воображения. Не обращайте внимания на общепринятые ограничения, какими бы они ни были – фразеологическими или же символическими. Создайте нужный вам образ задачи и увидьте правильное решение: очень возможно, что это произойдет.
• Аналогии фантастические. Что вы видите в свои самых смелых мечтах? А почему вы считаете, что это неосуществимо? Вспомните, сколько идей из произведений писателей-фантастов нашли свое применение в нашей жизни! Что же мешает фантазировать вам? Нужно лишь изложить свои фантастические аналогии – и сделать шаг к тому, чтобы они воплотились в жизнь!

Белки и кролики

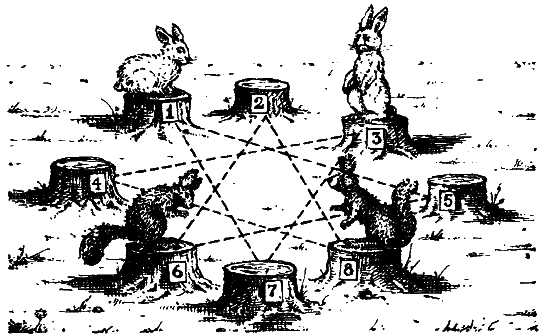
Перед вами восемь перенумерованных пней. На пнях 1 и 3 сидят кролики, на пнях 6 и 8 — белки. И белки, и кролики почему-то недовольны своими местами и хотят обменяться пнями: белки желают сидеть на местах кроликов, а кролики — на местах белок. Попасть на новое место они могут, прыгая с пня на пень по следующим правилам:
1) прыгать с пня на пень можно только по тем линиям, которые показаны на рисунке; каждый зверек может делать несколько прыжков кряду;
2) два зверька на одном пне поместиться не могут, поэтому прыгать можно только на свободный пень. Имейте также в виду, что зверьки желают обменяться местами за наименьшее число прыжков. Впрочем, меньше чем 16 прыжками им не обойтись.
Как же они это сделают?

P.S. Задачу удобно решать с помощью скрипта, написанного одним из наших посетителей — http://kokoscripts.ucoz.ru/index/belki_i_kroliki/0-14

Находчивый альпинист

Один аль­пи­нист неудач­но спу­стил­ся с горы и насту­пил сра­зу на двух змей — коб­ру и гадю­ку. Одна из них его уку­си­ла, какая — неиз­вест­но. У него были с собой про­ти­во­ядия, по две таб­лет­ки каж­до­го вида: про­тив коб­ры и про­тив гадю­ки. Одну таб­лет­ку нуж­но при­нять сра­зу после уку­са, а дру­гую — на сле­ду­ю­щий день.

Аль­пи­нист вытрях­нул из упа­ков­ки на ладонь одну таб­лет­ку от коб­ры (K), стал вытря­хи­вать таб­лет­ку от гадю­ки (Г), но рука дрог­ну­ла и из упа­ков­ки Г выпа­ли обе таб­лет­ки. Теперь у него в руке три абсо­лют­но оди­на­ко­вые таб­лет­ки: одна K, две Г. А ему нуж­но немед­лен­но при­нять одну K и одну Г, оста­вив по вто­рой таб­лет­ке каж­до­го про­ти­во­ядия на зав­тра. Что ему делать?

Решение

Если таб­лет­ки никак нель­зя отли­чить друг от дру­га, зна­чит, надо при­ду­мать такое реше­ние, кото­рое не потре­бу­ет ана­ли­за всех таб­ле­ток.

Зада­ча аль­пи­ни­ста — при­нять одну таб­лет­ку от уку­са коб­ры и одну от уку­са гадю­ки. На ладо­ни лежат три таб­лет­ки, и если мы возь­мём любые две, то есть веро­ят­ность, что нам попа­дут­ся две таб­лет­ки от гадю­ки и тогда про­ти­во­ядие от коб­ры не сра­бо­та­ет (аль­пи­нист же не зна­ет, какая имен­но змея его уку­си­ла). Зна­чит, нам такой вари­ант не под­хо­дит.

Что­бы сего­дня и зав­тра при­нять оди­на­ко­вые пор­ции, аль­пи­ни­сту нуж­но к этим трём таб­лет­кам доба­вить чет­вёр­тую, раз­ло­мать их все попо­лам и раз­не­сти эти поло­вин­ки по двум раз­ным куч­кам. Смысл в том, что­бы в каж­дой куч­ке лежа­ло по одной поло­вин­ке от каж­дой таб­лет­ки. Тогда в обе­их будет по две поло­вин­ки таб­лет­ки от коб­ры и по две поло­вин­ки таб­лет­ки от гадю­ки, а две поло­ви­ны дают как раз целую таб­лет­ку.

Полу­ча­ет­ся, что ему сего­дня и зав­тра нуж­но съесть по 4 поло­вин­ки, по одной от каж­дой таб­лет­ки.

Любите логику? На этом можно заработать

В ИТ сей­час одни из самых высо­ких зар­плат. Осва­и­вай­те любую ИТ-специальность, кото­рая вам по душе, и ста­но­ви­тесь бога­че. В «Прак­ти­ку­ме» — билет в про­фес­сию айтиш­ни­ка, при­хо­ди­те.
Логич­но!

Решение задач на проценты: метод пропорции

Еще один способ решения задач на проценты – это метод пропорции. Это наиболее простой способ решения таких задач.

Напомним, что пропорция – это равенство двух отношений:

Для нас важно основное свойство пропорции, которое заключается в том, что произведение крайних членов пропорции равно произведению средних членов. Проще запомнить, что мы можем перемножить члены пропорции крест-накрест:

При решении задач на проценты с помощью метода пропорции необходимо руководствоваться следующим правилом:

всё – 100%

часть – часть в %

Далее записываем пропорцию: 

Давайте решим приведенные выше примеры задач на проценты с помощью метода пропорции.

Задача 4

В городе проживало 30 000 человек. В результате строительства нового микрорайона количество жителей увеличилось на 6%. Сколько человек стало проживать в городе?

Решение: Итак, в городе проживало 30 000 человек и это всё его население, т.е. 100%. Так и запишем:

30 000 – 100%

Далее население выросло на 6%, т.е. всё его население стало составлять 100% + 6% = 106% и нам неизвестно, сколько это человек, т.е. Х человек. Запишем:

Х – 106%

Таким образом, получаем:

30 000 – 100%

Х – 106%

Составим пропорцию: Правую дробь пропорции можно сократить на 2, получим: Теперь воспользуемся основным свойством пропорции и перемножим ее члены крест-накрест:

30 000 * 53 = 50х

Далее обе части полученного уравнения мы можем разделить на 50, получим:

600 * 53 = Х

Х = 31 800

Ответ: 31 800 человек

 Задача 5

Сколько килограмм яблок нужно собрать, чтобы получить из них 5 килограмм сушеных яблок, если известно, что в свежих яблоках содержится 90% воды?

Решение: Нам неизвестно первоначальное количество всех яблок (всё количество), т.е. это Х, которое составляет 100%. Количество сушеных яблок (часть от первоначального количества яблок) составляет 5 кг. Причем известно, что количество сушеных яблок на 90% меньше от первоначального количества яблок (т.к. 90% — это вода, которая из них испарилась). Следовательно, количество сушеных яблок составит 100% — 90% = 10%. Запишем наши рассуждения:

Х – 100%

5 – 10%

Запишем наши рассуждения: Сократим правую дробь на 10, получим:Воспользуемся основным свойством пропорции и перемножим ее члены крест-накрест:

Х = 10 * 5

Х = 50

Ответ: 50 кг

Задача 6

Холодильник стоимостью 20 000 рублей был продан спустя месяц за 22 000 рублей. На сколько процентов увеличилась стоимость холодильника?

Решение: Нам известно, что исходная цена – 20 000 рублей, следовательно, 20 000 рублей – это 100%. Тогда конечная цена 22 000 рублей – это неизвестное количество процентов, т.е. Х%. Так и запишем:

20 000 – 100%

22 000 – Х%

Теперь запишем пропорцию: Сократим левую дробь на 2 000, получим: Воспользуемся основным свойством пропорции, то есть перемножим ее члены крест-накрест:

10Х = 1 100

Х = 110

В результате решения мы получили результат 110%, но он не является ответом! Ведь нам нужно найти, на сколько процентов изменилась стоимость холодильника. Чтобы это узнать, нужно из полученного числа процентов отнять 100%:

110% — 100% = 10%

Ответ: 10%

Задачи на движение

Пример 1

Расстояние между двумя городами 125 километров. В одно и то же время выезжают два велосипедиста навстречу. Скорость первого велосипедиста 10 км/ч. Второй едет со скоростью 15 км/ч. Через какое время они встретятся?

Решение

• Начинаем с составления краткого условия. Лучше всего оформить в качестве таблицы;
• Велосипедиста два— значит нужны 2 строки. Столбцов стандартно 3. Но в этом типе задач у нас будут общие показатели. То есть, расстояние и время всегда одно сразу для всех строк;
• Заполняем таблицу числами. Что должно получится смотрите в ниже;

Таблица 5 — краткое условие

	Скорость	Время	Расстояние
1 велосипедист	10	?	125
2 велосипедист	15	?	125

• Теперь переходим к расчётам. Логично, что для встречи велосипедисты должны проехать в сумме весь путь. Необязательно одинаковое расстояние, так как оно зависит от скорости каждого из них;
• Нам нужно посчитать какое расстояние они преодолевают в час. Для этого сложим скорости первого и второго. Получаем выражение: 10+15=25 км/ч;
• Для расчёта времени через которое они встретятся нужно воспользоваться формулой T=S:V. Подставляем числа и получаем выражение: 125:25=5 ч;
• Соответственно, велосипедисты пересекутся между собой через 5 часов. Записываем это в ответ.

Пример 2

Расстояние, на котором между собой находятся два города — 600 км. Из них одновременно на встречу друг другу выехали два автомобиля. В пути они встретились через 5 часов. Найдите скорость первого автомобиля, если известно, что второй ехал со скоростью 80 км/ч.

Решение

• Составим таблицу, в которой ситуация из условия будет наглядно представлена;
• Два автомобиля — две строки. Стандартное количество столбцов — три;
• Заполняем числами из условия. Что должно получится, смотрите ниже;

Таблица 6 — краткое условие

	Скорость	Время	Расстояние
1 автомобиль	?	5	600
2 автомобиль	80	5	600

• Переходим к расчётам. Для нахождения скорости первого автомобиля нам нужно знать, сколько километров он проехал. Найти это можно, вычтя из общего пути расстояние, которое проехал второй до их встречи;
• Используем формулу S=VT. Подставляем числа из таблицы, получаем выражение: 80×5=400 км. Это расстояние прошёл второй автомобиль до встречи с первым. Значит, первый проехал всего: 600-400=200 км;
• Теперь можно найти скорость первого автомобиля. Используем формулу V=S:T. Подставляем числа: 200:5=40 км/ч;
• Полученное значение — ответ на главный вопрос задачи. Записываем его.

Если вас смущает время, которое написано один раз для всех объектов, то можно поступить следующим образом. Записывайте его отдельно к каждой строке и рядом нарисуйте отрезок, который снизу отмечен расстоянием, а сверху подписан временем.

Поиски вируса

В лаборатории имеется некоторое количество проб крови, взятых у различных людей. Одна из них содержит весьма разновидность вируса, определяемую при помощи дорогостоящих и трудоемких исследований. Чтобы уменьшить число исследований, лаборатория обратилась за консультацией к математику. Ему пояснили, что при анализах можно брать части различных проб, смешивать их и определять, присутствует ли вирус в полученной смеси. Узнав общее исследуемых людей (оно оказалось между 100 и 200), математик предложил исследовать сначала одну любую из имеющихся проб, утверждая, что общее число анализов при этом все же будет минимальным. Сколько проб в лаборатории?