Конспект занятия по математике в подготовительной группе «геометрические фигуры»

Фигура тетраэдр: описание

Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.

Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 — 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a3*√2/12 и S = √3*a2, где a — длина стороны равностороннего треугольника.

Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH₄, в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.

Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.

Треугольник Рело

Как ни удивительно звучит, но с помощью дрели можно просверлить квадратное отверстие, а помогает в этом треугольник Рело. Он представляет собой область, образованную посредством пересечения 3 равных окружностей, центры которых являются вершинами правильного треугольника, а радиусы равны его стороне.

Сам треугольник Рело назван по фамилии немецкого ученого-инженера, который первым наиболее детально исследовал его особенности и использовал для своих механизмов на рубеже XIX-XX в. в., хотя его удивительные свойства были известны еще Леонардо да Винчи. Кто бы ни был его первооткрывателем, в современном мире эта фигура нашла широкое применение в виде:

• сверла Уаттса, которое позволяет сверлить отверстия практически идеальной квадратной формы, только с чуть закругленными краями;
• медиатора, необходимого для игры на музыкальных щипковых инструментах;
• кулачковых механизмов, используемых для создания зигзагообразных швов в швейных машинах, а также немецких часах;
• стрельчатых арок, характерных для готического стиля в архитектуре.

Невозможные фигуры 

Отдельного внимания заслуживают так называемые невозможные фигуры – удивительные оптические иллюзии, которые на первый взгляд кажутся проекцией трехмерного объекта, но при ближайшем рассмотрении становятся заметны необычные соединения элементов. Наиболее популярными из их числа являются:

Трибар, созданный отцом и сыном Лайонелом и Роджером Пенроузами, который представляет собой изображение равностороннего треугольника, но имеет странные закономерности. Стороны, образующие верхнюю часть треугольника кажутся перпендикулярными, но правая и левая грани в нижней части также кажутся перпендикулярными. Если рассматривать каждую часть этого треугольника по отдельности, еще можно признать их существование, но в действительности такая фигура существовать не может, поскольку при ее создании были неправильно соединены правильные элементы.

Бесконечная лестница, авторство которой также принадлежит отцу и сыну Пенроузам, поэтому ее часто называют по их имени – «лестницей Пенроуза», а также «Вечной лестницей». На первый взгляд, она выглядит как обычная, ведущая вверх или вниз лестница, но при этом человек, шагающий по ней будет непрерывно подниматься (против часовой стрелки) или опускаться (по часовой стрелке). Если визуально путешествовать по такой лестнице, то по окончании «путешествия» взгляд останавливается в точке начала пути. Если бы такая лестница существовала в действительности, по ней пришлось бы подниматься и спускаться бесконечное число раз, что можно сравнить с бесконечным сизифовым трудом.

Невозможный трезубец – удивительный объект, глядя на который невозможно определить, где начинается средний зубец. Он также основан на принципе неправильных соединений, которые могут существовать только в двухмерном, но не трехмерном пространстве. Рассматривая части трезубца по отдельности, с одной стороны видны 3 круглых зуба, с другой стороны – 2 прямоугольных.

Таким образом, части фигуры вступают в своеобразный конфликт: во-первых, происходит смена переднего и заднего плана, во-вторых круглые зубцы в нижней части трансформируются в плоские в верхней.

Геометрические аппликации: пошаговые инструкции для дошкольников

Для разного возраста дошкольников создание аппликаций из фигур отличаются друг от друга:

• До достижения ребенком 5 лет вырезание из бумаги производят взрослые, а приклеивание фигур уже можно доверить детям.
• До пятилетнего возраста детей неровно вырезанные ими детали придется исправлять родителям или воспитателям.
• За ребенком, которому исполнилось 5 лет, уже можно только наблюдать.

Младшие дошкольники увиденные формы всегда упрощают. Так, например, пышные облака они изображают в виде обыкновенных овалов.

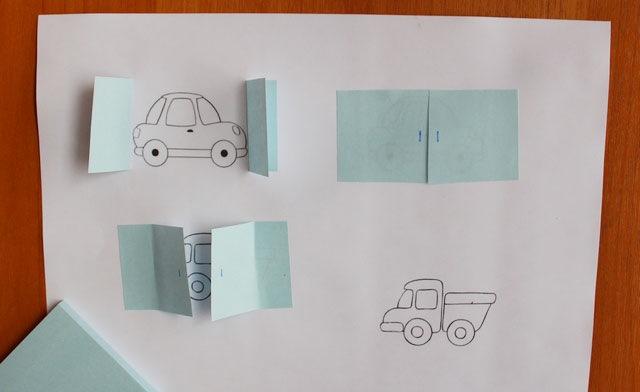
Аппликация Гараж для дошкольников

Геометрические фигуры объемные, как и простые, подходят для аппликаций, если они бумажные. Их легко формировать в группы, создавая еще более сложные тела, а потом приклеивать к картону. После этого такие поделки становятся наглядным пособием для дальнейшего обучения.

Для аппликации Гараж дети должны изобразить его на бумаге, при этом им можно предложить сделать:

• квадратные двери;
• треугольную крышу;
• аркообразные ворота.

Геометрические фигуры из бумаги — пример объемной фигуры — гараж

Потом дошкольники должны вырезать детали гаража и приклеить их к картону. Далее они могут таким же образом соорудить машину, которую необходимо поместить в готовый гараж после этого.

Чтобы вместе с ребенком создать аппликацию Животное, для него необходимо вырезать образцы маленьких деталей зверя.

Так, для кошки подойдут:

• круги вместо глаз;
• овалы для головы и туловища;
• треугольники для ушей.

Подготовленные взрослым шаблоны дошкольник потом сам соберет в форме кошки и наклеит их на основу. В результате должна получиться бумажная композиция на тему животное с приклеенными геометрическими фигурами в качестве деталей аппликации. Маленькие дети, играя с фигурными шаблонами, развивают свои творческие способности и мелкую моторику.

Образцы для аппликаций необходимо:

• формировать в цветной эскиз;
• складывать по предлагаемому примеру;
• приклеивать на заданную поверхность.

Для создания бумажных композиций из геометрических фигур также понадобятся:

• расходные материалы для аппликаций;
• клей-карандаш;
• база для основы в виде деревянного бруска или картона;
• удобные детские ножницы с неострыми концами.

Перед занятиями аппликацией для детей тщательно подготавливают их рабочие места:

• проверяют поверхности на безопасность;
• удаляют все отвлекающие от работы предметы;
• застилают стол газетами или клеенкой;
• устраняют все, что может принести дискомфорт в процессе труда;
• снабжают рабочее место дополнительными инструментами.

При создании аппликаций дети обучаются:

• быть аккуратными и усидчивыми;
• распознавать геометрические формы;
• творчески мыслить;
• взаимодействовать с коллективом;
• азам конструкторского дела;
• кропотливой работе.

Взрослым при совместных упражнениях с дошкольником придется:

• все правильно организовать;
• вести занятия в игровой манере для удержания детского интереса;
• для формирования тактильного восприятия применять различные материалы;
• подбирать тему под определенный детский возраст;
• давать ребенку высказываться и анализировать вместе с ним его ошибки;
• стимулировать детскую фантазию и самостоятельность.

Геометрические объемные тела

Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:

1. Они ортогональны друг другу, то есть перпендикулярны.
2. Эти оси нормализированы, то есть базисные вектора каждой оси имеют одинаковую длину.
3. Любая из осей координат — это результат векторного произведения двух других.

Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:

1. Класс полиэдров. Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань — это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней — это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
2. Класс круглых тел или тел вращения. Эти фигуры имеют хотя бы одну поверхность, образующую их, изогнутой формы. Например, шар, конус, цилиндр, тор.

Что касается свойств объемных фигур, то следует выделить два самых важных из них:

1. Наличие определенного объема, который фигура занимает в пространстве.
2. Наличие у каждой объемной фигуры площади поверхности.

Оба свойства для каждой фигуры описываются конкретными математическими формулами.

Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.

Рисование в перспективе: куб

Обычно применяется белая гипсовая модель, на которой отчетливо видна светотень. Модель лучше приобрести или сделать самостоятельно, фотографию использовать не рекомендуется.

Для изображения необходимо:

• Наметить местоположение фигуры. Разместить ее немного выше центра листа, при этом она должна быть подвинута в сторону теневой области. Это способствует равновесию композиции.
• Провести первую вертикальную линию. Это будет ближайшее к зрителю ребро куба. Засечками нужно ограничить высоту куба.
• Изобразить основание фигуры. Начинать необходимо с видимых линий, точно определив углы их наклона.
• Нарисовать линии, располагающиеся вверху. Перед этим необходимо вспомнить принципы линейной перспективы. Один из них гласит: видимый размер фигур при удалении становится меньше. Линия горизонта располагается на уровне глаз, однако при изменении положения головы эта линия может подняться или опуститься.

Рисунок геометрических фигур карандашом: куб

• Определить, как сократились боковые грани фигуры.
• Нарисовать дальние линии, не забывая про линии, которые не видны.
• После выполнения и проверки построения выделить ближайшие линии. Чем они ближе, тем более темными их следует сделать.
• Выполнить штриховку. Сначала заполнить штрихом теневые области, а затем перейти к освещенной поверхности. Ближний угол следует оставлять незаштрихованным, а дальнюю часть заполнить легким штрихом.
• Подчеркнуть объем формы, сделав тональные акценты.

ТРЕУГОЛЬНИК В КОМПОЗИЦИИ

Треугольник — наиболее часто встречающаяся в природе форма. Треугольник — самая динамичная, неустойчивая форма, которая ассоциируется с движением, развитием, скоростью. В положении «вершиной вверх» вызывает образы устойчивости, стабильности (пирамида). Несколько треугольников — позитивное динамическое движение. В положении «вершиной вниз» – шаткое равновесие, балансировка. В отличие от прямоугольника, стороны не противостоят друг другу, а меняют направление развития. Это может быть использовано для создания конкретных образов. Треугольник естественным образом вносит в композицию ощущение глубины пространства.

Фото: Josh Johnson

Клеим

Использовать геометрические фигуры в занятиях по аппликации можно хоть с самого первого занятия. Когда малыш только знакомится с клеем (на мой взгляд, знакомство хорошо проходит в возрасте от 1 года 2-3 месяцев), ему больше интересен сам процесс приклеивания, нежели создание какой-то композиции. Поэтому не стоит в первых аппликациях с малышом создавать сложные картины, начните просто с хаотичного приклеивания бумажек на листочек, а еще лучше с хаотичного приклеивания геометрических фигур! Пока малыш увлечено мажет фигурку клеем (с вашей помощью) и прикладывает ее на листочек, вы говорите ему, как она называется. При такой игре все названия очень хорошо укладываются у малыша в голове, можно сказать, прочно «приклеиваются»

Когда у крохи уже будет получаться приклеивать элементы аппликации на заданные места (примерно с 1,5 лет), можно попробовать создать простую композицию.

Вы также можете в своих занятиях использовать различные готовые пособия, например:

Школа семи гномов 1+. Форма, цвет (Ozon, My-shop)

Развивающие наклейки для малышей. Форма (Ozon, My-shop)

Чудесные наклейки. Веселая геометрия (Ozon, My-shop)

Определяем свой тип телосложения

Физиологи и спортивные врачи четко разграничивают три основных типа телосложения, однако в реальной жизни большинство людей трудно отнести к одному из них. На практике соматотипы часто смешиваются, что определяет наличие у конкретного атлета разных отличающихся характеристик.

Рассмотрим основные черты «чистых» соматотипов:

1. Эктоморф

   – худое тело с тонкими, но длинными костями, минимальное количество жировой ткани и невыразительный мышечный корсет.

2. Эндоморф

   – более выраженная мускулатура, вместе с которой в организме имеется значительное количество жировой ткани.

3. Мезоморф

   – массивное телосложение, сильная и хорошо очерченная от природы мускулатура, толстые кости. Легко набирают мышечную массу, однако при малейших перекосах в диете появляется лишний вес в виде жира.

Одной из главных характеристик, указывающих на тип телосложения, является толщина кости. Именно по ней можно определить собственный соматип, для этого замерьте обхват кисти, если он превышает 20 см – вы эндоморф, меньше 17-ти см – эктомоф, 17-20 см – мезоморф.

Узнайте больше:

Эктоморфный соматотип

Телосложение эктоморфов предопределено быстрым обменом веществ, за счет которого они могут употреблять большое количество пищи, включая продукты непосредственно приводящие к набору жира, и не толстеть. Это одновременно является и преимуществом, и главным минусом эктоморфов, поскольку набор мышечный массы при занятиях в тренажерном зале им дается крайне сложно. Однако грамотно построенные тренировки и выверенный рацион питания позволяют эктоморфам прогрессировать и впоследствии получать атлетическую фигуру с тонкой талией и широкими плечами.

Основные правила тренинга эктоморфов:

Около 75% успеха в тренировках эктоморфов зависит от питания. Им необходимо употреблять большое количество источников медленных углеводов, объем которых должен составлять не менее 50% от общей калорийности рациона. Рекомендованное количество белка – 3 грамма на килограмм веса тела, профицит калорий в день как минимум 700-800 ккал.

Мезоморфный соматотип

Мезоморф является общепринятым типом нормального телосложения, такие люди отличаются сравнительно широким костяком и выраженной мускулатурой даже без тренировок на гипертрофию мышц. Единственный недостаток мезоморфов – склонность к набору жира, что происходит при несбалансированном питании.

Преимуществом мезоморфов является то, что для достижения результатов в тренажерном зале им нужно прикладывать значительно меньше усилий, чем атлетам с другими соматотипами. Они будут прогрессировать при любой адекватной программе тренировок, будь то сплит либо фуллбади.

Принципы тренинга мезоморфов:

Проще мезоморфам и в плане питания. Им можно употреблять любые высококалорийные продукты, необходимо лишь следить за тем, чтобы доля жиров в рационе не превышала 20% от калорийности, и не увлекаться быстрыми углеводами (мучным и сладким).

Изучение геометрических фигур: названия, форма, цвет, размер

С простыми фигурами и их цветами детей знакомят с 2 до 3 лет. Обучение должно происходить ненавязчиво, в форме рассказа или развлечения.

На помощь могут прийти:

• сортер;
• игрушки с деревянными вкладышами;
• картинки.

К 2 годам ребенок должен знать основные геометрические фигуры и цвета

С 2 лет дети должны знать такие цвета и геометрические фигуры, как:

• белый;
• зеленый;
• желтый;
• красный;
• синий;
• розовый;
• черный;
• фиолетовый;
• оранжевый;
• круг;
• квадрат;
• треугольник;
• овал;
• прямоугольник;
• полукруг.

Геометрические фигуры объемные можно и необходимо изучать в игровой форме, чтобы вызвать у детей интерес. Ведь развлекательный момент ознакомления с различными формами значительно облегчает весь следующий образовательный процесс

Вместе с этим дети учатся заострять внимание только на необходимом и проявлять самостоятельность

Пример обучения детей геометрическим фигурам в игровой форме

Хронология обучения дошкольников простой начертательной геометрии будет следующей:

• изображенные на плотной бумаге разные фигуры, отличающиеся по цвету и размеру, называют и проговаривают вместе с ребенком;
• обведение очертаний фигур на картоне и последующее их разукрашивание определенными цветами, сравнение размеров изображений;
• вырезанные фигуры располагают по разным местам дома, чтобы дети потом их находили и называли, проговаривая также размер и цвет;
• предложение поиграть с разными мозаиками и пирамидками из геометрических фигур;
• отождествление с другими предметами в окружающей среде.

Способов изучения геометрических фигур предостаточно, среди них выделяются:

• наблюдающий, когда детей знакомят с вырезанными из картона образцами форм, а потом спрашивают о них;
• сравнительный, при котором дошкольники рассматривают парные карточки с фигурами и отмечают их отличия и схожесть;
• закрепительный, заключающийся в опросе детей о пройденном материале.