Интересные задания по математике: игры и задания с ответами для школьников

Как сделать разбор сложного предложения

Чтобы составить схему сложного предложения, нужно сначала найти все его основы. Это поможет понять, сколько в нем частей, после этого можно будет найти, как они между собой связаны. Рассмотрим это на примере.

В этом предложении две основы (ребята гуляли, снег пошел), которые соединены между собой интонацией, что на письме отражается в виде запятой. Союза между этими частями нет.

В сложном предложении не обязательно должно быть строго две грамматических основы: их может быть три и даже больше.

В основном порядок частей в сложном предложении последовательный: сначала идет главная часть, за ней следует та, которая связана с ней по смыслу. В предложениях, которые связаны интонацией и представляют собой просто перечисление событий, часто нет главной и присоединенной части – их порядок можно поменять местами и смысл предложения от этого совершенно не изменится.

Это легко понять, если сравнить два сложных предложения с одинаковыми основами, которые просто переставлены местами:

• Веет ветер, моросит дождик.
• Моросит дождик, веет ветер.

Очевидно, что от перестановки частей смысл предложения совершенно не поменялся: оно рассказывает о погоде, описывая ее с разных сторон.

Такой принцип роднит сложные предложения с максимально простой структурой с примерами на сложение, где от перестановки мест не изменяется итоговая сумма, что говорит о том, что язык в какой-то степени математичен.

Алгоритм разбора любого предложения, в котором две и больше основ, одинаковый: нужно найти эти основы и определить, соединены ли они только интонацией, то есть знаком препинания, или в установлении связи между ними участвовал союз.

Что мы узнали?

Определение сложного предложения само по себе достаточно простое: это такая единица языка, в которую входит не одна грамматическая основа, а несколько (как минимум две и больше). Эти части могут соединяться только интонацией (знаком препинания) или интонацией и союзом. Чтобы разобрать сложное предложение, нужно сначала найти все его основы, а потом определить, каким образом они соединены между собой. Это достаточно простой и понятный алгоритм.

Математика 4 класс

В четвертом классе идет активная работа с единицами измерения: длина (см, дц, м, км), масса (г, кг), время (с, ч), скорость (м/c, км/ч). А также соответственно работа с предыдущими операциями.

Идет изучение математических уравнение с одним неизвестным.

Примеры для тренировки:

Задание №1:

Задание №2:

1. Человек на велосипеде преодолел расстояние от города до деревни, равное 60 км, за 4 часа. На обратном пути он сбавил скорость на 3 км/ч. Сколько времени потратил велосипедист на поезду?

2. 16ти часовой путь самолета имеет длину 4150 км. Самолет летел 3 ч со скоростью 660 км/ч и еще 2 часа со скорость 730 км/ч. Какое расстояние предстоит преодолеть самолету за последний час?

3. За 5 часов кукурузник пролетел 220 км. Какое расстояние преодолеет кукурузник, если скорость увеличить на 7км/ч?

Геометрия в пространстве (стереометрия)

Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара:

Площадь поверхности шара (или, другими словами, площадь сферы):

10 примеров сложных предложений из русской литературы

Однажды осенью матушка варила в гостиной медовое варенье, а я, облизываясь, смотрел на кипучие пенки.А.С. Пушкин. «Капитанская дочка»

Уж солнце начинало прятаться за снеговой хребет, когда я въехал в Койшаурскую долину.М.Ю. Лермонтов. «Герой нашего времени»

Покамест слуги управлялись и возились, господин отправился в общую залу.Н.В. Гоголь. «Мертвые души»

Раздался крик команды, опять полк звеня дрогнул, сделав на караул.Л.Н. Толстой. «Война и мир»

Петр глянул в сторону, куда указывал барин.И.С. Тургенев. «Отцы и дети»

Сегодня утром вспомнила, что я именинница, и вдруг почувствовала радость, и вспомнила детство, когда еще была жива мама.А.П. Чехов. «Три сестры»

Когда лошади стали, он выкинул из тарантаса ногу в военном сапоге с ровным голенищем и, придерживая руками в замшевых перчатках полы шинели, взбежал на крыльцо избы.И.А. Бунин. «Темные аллеи»

Жизнь Берлиоза складывалась так, что к необыкновенным явлениям он не привык.М.А. Булгаков. «Мастер и Маргарита»

Темные деревья дремали раскорячившись, объятые лаской спокойного дождя; им было так хорошо, что они изнемогали и пошевеливали ветками без всякого ветра.А.П. Платонов. «Чевенгур»

Хозяйка пришла звать его к телефону, и он, вежливо сутулясь, последовал за ней в столовуюВ.В. Набоков. «Дар»

Запятые и другие знаки препинания в сложных предложениях

В сложносочиненных предложениях запятая ставится между частями предложения перед союзами:

• и, да, ни… ни

• а, но, однако

• или, либо, или… или,

• да, да и, тоже, также

• то есть, а именно

Пример: Ты всегда был строг ко мне, и ты был справедлив.

В сложносочиненных предложениях запятая НЕ ставится:

Перед союзами и, да (в значении и), или, либо запятая не ставится, если части предложения объединены каким-либо общим элементом (второстепенным членом или придаточным предложением):Вскоре после восхода набежала туча и брызнул короткий дождь

• Между двумя назывными предложениями:Хриплый стон и скрежет ярый.

• Между двумя вопросительными, восклицательными, побудительными предложениями:Это кто такие и что им надобно?

• Между двумя неопределенно-личными предложениями, если подразумевается общий производитель действия:Стали искать черкесов во всех углах и, разумеется, ничего не нашли.

• Между двумя безличными предложениями, имеющими синонимичные слова в составе сказуемого:Нужно собирать вещи и необходимо предупредить всех об отъезде.

Подробнее о пунктуации в сложносочиненных предложениях.

В сложноподчиненных предложениях главная и придаточные части отделяются запятой, точкой с запятой или тире.Пример: Он явился с известием, что лошади готовы.

• Если придаточное предложение находится внутри главного, оно выделяется с обеих сторон.Капустин обещал договориться с начальником школы, чтобы он увеличил Мересьеву число вылетов, и предложил Алексею самому составить себе программу тренировок.

• Если главная часть сложноподчиненного предложения находится внутри придаточной, то запятая обычно ставится только после главной части:Хозяйством нельзя сказать, чтобы он занимался…

Между главной и следующей за ней придаточной частью запятая не ставится:

• Если перед подчинительным союзом или союзным словом стоит отрицательная частица «не».В море, в качке, спишь не когда хочешь, а когда можешь.

• Если перед подчинительным союзом или союзным словом стоит сочинительный союз и, ни … ни, или, либо.Он не слышал ни как сестра вошла в комнату, ни как потом бесшумно вышла.

• Если придаточная часть состоит из одного союзного слова (относительного местоимения или наречия).Я бы тоже желал знать почему.

• Если имеется несколько относительных слов, выступающих в роли однородных членов предложения:Позвонят — расспроси кто и зачем.

Подробнее о пунктуации в сложноподчиненных предложениях.

В бессоюзных предложениях могут использоваться запятые, точка с запятой, тире, двоеточие.Была без радости любовь, разлука будет без печали. Привычка, свыше нам дана: замена счастию она.

Подробнее о пунктуации в бессоюзных предложениях.

Виды сложных предложений: характерные особенности и примеры

Для начала необходимо изучить таблицу с примерами “Виды сложных предложений”:

Из таблицы понятно, что в сложном предложении больше одной основы, характер отношений между ними может быть очень разным. Они делятся на две большие группы – с союзами и без них, а союзные предложения, в свою очередь, делятся на сложноподчиненные и сложносочиненные в зависимости от характера связи и использованных союзов. А поскольку в русском языке все не так просто, есть еще одна группа – сложные предложения, в которых простые связываются между собой разными видами связи.

Сложное предложение, вне зависимости от вида связи, может состоять не только из двух простых, но и больше. Чтобы правильно определить тип такого предложения, нужно найти грамматические основы и определить границы простых предложений, а потом выяснить характер связи между ними.

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Быстрый счет»

Игра «быстрый счет» поможет вам усовершенствовать свое мышление. Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Математические матрицы»

«Математические матрицы» великолепное упражнение для мозга детей, которое поможет вам развить его мыслительную работу, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке ниже данное число «29», а искомая пара «5» и «24».

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Аналитическая геометрия

Пример 16. Уравнение плоскости, проходящей через точку перпендикулярно вектору

Написать уравнение плоскости, проходящей через точку M перпендикулярно вектору .Дано:
Координаты точек: M(2, 5, -3), M₁(7, 8, -1) и M₂(9, 7, 4).Найти:
Уравнение плоскости, проходящей через точку M перпендикулярно вектору .

Решение:
В качестве нормального вектора плоскости выбираем вектор = {x₂-x₁, y₂-y₁, z₂-z₁} = {9-7, 7-8, 4-(-1)} = {2, -1, 5}.

Уравнение плоскости, проходящей через точку M(x, y, z) перпендикулярно вектору = {A, B, C}, имеет вид .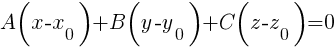

Составляем уравнение плоскости с нормальным вектором = {2, -1, 5}, проходящей через точку M(2, 5, -3):.

Ответ: .

Пример 17. Уравнение плоскости «в отрезках»

Какие отрезки отсекает на осях координат плоскость?Дано:
Уравнение плоскости: 2x – 4y + 6z – 12 = 0.Найти:
Отрезки, которые отсекает на осях координат плоскость.a, b, c — ?

Решение:
Приведем общее уравнение плоскости к виду уравнения «в отрезках»:

Уравнение — это уравнение плоскости «в отрезках». Параметры представляют собой координаты точек пересечения плоскости с координатными осями и равны (с точностью до знака) отрезкам, отсекаемым плоскостью на координатных осях.

Применяя вышеприведенное к уравнению 2x – 4y + 6z –12 = 0, получим:.

Отрезки, отсекаемые на осях, равны a = 6, b =−3, c = 2.
Отрицательный знак перед b показывает, что плоскость пересекает отрицательную полуось Oy.

Задачи по теме «Уравнение плоскости в пространстве»

Задача 1. Составить канонические уравнения прямой:

Решение:
Для составления канонического или параметрического уравнения прямой в пространстве, нужно знать координаты какой-либо точки, лежащей на этой на этой прямой, и координаты вектора, коллинеарного прямой.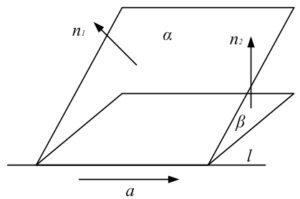
Так как прямая является линией пересечения двух плоскостей, ее направляющий вектор а параллелен каждой из этих плоскостей и соответственно перпендикулярен нормалям n₁ и n₂ к данным плоскостям. В таком случае он коллинеарен векторному произведению [n₁, n₂].n₁ = (2; 1; -5), n₂ = (5; 3; 8), [n₁, n₂] = (23; -41; 1).
Итак, (l; m; n) = (23; -41; 1).

Найдем точку, лежащую на данной прямой, у которой одна из координат принимает выбранное нами значение; тогда остальные две координаты можно определить из системы уравнений, задающей пересекающиеся плоскости.

Примем для удобства вычислений z = 0, тогда для точки A={х; у; 0}x = -4; y = 11; A = {4; 11; 0}.

Cоставим канонические уравнения данной прямой:.

Ответ: .

Задача 2. Составить уравнение плоскости, проходящей через прямую k: и точку B = {2; -3; 1}.

Решение:
Так как точка А = {-3,5,-1} принадлежит плоскости, значит вектор AB параллелен плоскости.
Так как данная прямая лежит в плоскости, ее направляющий вектор a = (2; 1; -1) параллелен плоскости.
Значит, нормаль к плоскости коллинеарна векторному произведению этих векторов.

Так как прямая лежит в плоскости, ее направляющий вектор a = (2; 1; -1) параллелен плоскости. При d = 0 из уравнений прямой получаем: — координаты точки А, принадлежащей прямой и соответственно плоскости.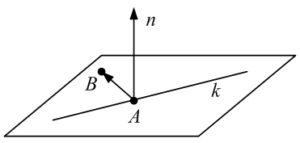

Получается, что вектор AB = (5; -8; 2) параллелен плоскости. Значит, нормаль n к плоскости коллинеарна векторному произведению = (-6; -9; -21).
Примем n = (2; 3; 7) и составим уравнение плоскости, проходящей через точку B перпендикулярно n: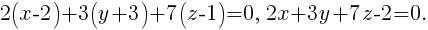

Ответ: 2x + 3y + 7z – 2 = 0.

Задача 3.Написать уравнение плоскости, которая проходит через три точки с координатами N₁(x₁, y₁, z₁), N₂(x₂, y₂, z₂), N₃(x₃, y₃, z₃).

Решение:
Предположим, что какая нибудь, находящаяся на плоскости точка N, имеет координаты (x, y, z). Для этого случая уравнение плоскости примет вид:
(r-r, a, b) = 0,
гдеr = (x, y, z);r = (x₁, y₁, z₁);
базисные векторы (смотрите рисунок) соответственно равны и .

Если записать смешанное произведение в виде определителя, то получим необходимое уравнение плоскости:

Ответ:

3 класс

В третьем классе продолжается отработка навыков счёта. Примеры становятся более сложными, и для их решения применяется решение в столбик. Для развития навыков быстрого счёта рекомендутся давать ученику большое количество разнообразных примеров. Их можно взять здесь:

Примеры на умножение в третьем классе включают уже двузначные числа. Также полезно отработать счёт с «опорными» числами, которые часто встречаются в различных расчётах.

Генератор примеров

Для отработки умения быстрого счёта ученикам требуется довести навыки сложения, умножения до автоматизма. Для этого рекомендуется решать большое количество однотипных, но разнообразных примеров — это позволяет ученика довести навыки дло автоматизма. Идеально, когда ученик выдаёт ответ не дадумываясь — «автоматически».

Примеры нашего генератора можно скопировать и перенести в другое приложение, можно распечатать с экрана выбрав рамер и шрифт. Примеры по математике можно распетатать в формате Word для раздачи ученикам.

Онлайн генератор примеров позволяет получить бесконечное количество примеров на любой случай. Ученик не ограниченный примерами из учебника получает возможность отработать навыки счёта сколько угодно раз. В конце концов — количество перерастает в качество. Надеемся, наш генератор примеров помождет вашим детям научиться быстро и правлиьно считать.

Генератор примеров по математике онлайн