Математика

Подписи к слайдам:

Слайд 1

Женщины математики Выполнила ученица 6а класса Собенина Мария

Слайд 4

С офия в асильева к овалевская

Слайд 5

м ария г аетана а ньези Мария Аньези была первой в мире женщиной , занимавшей должность профессора математики в университете .Она написала « Курс анализа для употребления Итальянского юношества», в котором даны оригинальные доказательства многих теорем . В ёе честь одна из кривых линий ,ёе Исследованных , поныне называется « кривой Аньези »

Слайд 6

Э мили, м аркиза дю Ш атле В 1706 году 17 декабря родилась Габриэль –Эмилия ле тонель де Бретей , позднее ставшая маркизой дю Шатле . Занимаясь самообразованием , маркиза дю Шате слелалась выдающимся математиком . Это был один из блистательнейших женских интеллектов века . Эмилия де Шатле была одной из тех женщин , чей вклад способствовал формированию курса матиматики . И хотя она не создала собственного оригинального учения ,её работа внес лазначительный вклад в развитие математической науки . «она была великим человеком , чья единственная вина состояла в том , что она – женщина »

Слайд 7

С офия ж ермен Так как родители не разрешали ей Заниматься матимакой , которой она увлекалась с детства , София тайком писала свои выкладки , по ночам под одеялом . За исследования по теории упругости София была присуждена в 1816г. премия парижской академии наук . Она отличалась также в области геометрии и теории чисел .

Примечания Править

1. Математика в профессиях. в каких профессиях нужна математика?

   Панов В. Ф. Математика древняя и юная. — Изд. 2-е, исправленное. — М.: МГТУ им. Баумана, 2006. — С. 581—582. — 648 с. — ISBN 5-7038-2890-2. (см. ISBN )

2. Словарь русского языка XI—XVII вв. Выпуск 9 / Гл. ред. Ф. П. Филин. — М.: Наука, 1982. — С. 41. (см. ISBN )

3. Декарт Р. Правила для руководства ума. М.-Л.: Соцэкгиз, 1936.
4. Маркс К., Энгельс Ф. Сочинения. 2-е изд. Т. 20. С. 37.
5. Бурбаки Н. Архитектура математики. Очерки по истории математики / Перевод И. Г. Башмаковой под ред. К. А. Рыбникова. М.: ИЛ, 1963. С. 32, 258.
6. Герман Вейль //
7. Государственный образовательный стандарт высшего профессионального образования. Специальность 01.01.00. «Математика». Квалификация — Математик. Москва, 2000 (Составлено под руководством О. Б. Лупанова)
8. Я. С. Бугров, С. М. Никольский. Элементы линейной алгебры и аналитической геометрии. М.: Наука, 1988. С. 44.
9. Н. И. Кондаков. Логический словарь-справочник. М.: Наука, 1975. С. 259.
10. Г. И. Рузавин. О природе математического знания. М.: 1968.
11. Ошибка скрипта

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать. После прохождения курса ребенок сможет:

После прохождения курса ребенок сможет:

1. В 2-5 раз лучше запоминать тексты, лица, цифры, слова
2. Научится запоминать на более длительный срок
3. Увеличится скорость воспоминания нужной информации

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Этимология Править

Слово «математика» произошло от др.-греч. μάθημα, что означает изучение, знание, наука, и др.-греч. μαθηματικός, первоначально означающего восприимчивый, успевающий, позднее относящийся к изучению, впоследствии относящийся к математике. В частности, μαθηματικὴ τέχνη, на латыни ars mathematica, означает искусство математики. Термин др.-греч. μᾰθημᾰτικά в современном значении этого слова «математика» встречается уже в трудах Аристотеля (IV век до н. э.). По мнению Фасмера в русский язык слово пришло либо через польск. matematyka, либо через лат. mathematica.

В текстах на русском языке слово «математика» или «маѳематика» встречается, по крайней мере, с XVII века, например, у Николая Спафария в «Книге избранной вкратце о девяти мусах и о седмих свободных художествах» (1672 год)

Философия математики Править

Основная статья: Философия математики

Цели и методы Править

Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного раздела математики — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.

Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.

Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. «Пространство $ \R^n $, при $ n>3 $ является математической выдумкой. Впрочем, весьма гениальной выдумкой, которая помогает математически разбираться в сложных явлениях».

Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.

Основания Править

Вопрос сущности и оснований математики обсуждался со времён Платона. Начиная с XX века наблюдается сравнительное согласие в вопросе, что надлежит считать строгим математическим доказательством, однако отсутствует согласие в понимании того, что в математике считать изначально истинным. Отсюда вытекают разногласия как в вопросах аксиоматики и взаимосвязи отраслей математики, так и в выборе логических систем, которыми следует при доказательствах пользоваться.

Помимо скептического, известны нижеперечисленные подходы к данному вопросу.

Теоретико-множественный подход Править

Основная статья: Теория множеств

Предлагается рассматривать все математические объекты в рамках теории множеств, чаще всего с аксиоматикой Цермело — Френкеля (хотя существует множество других, равносильных ей).
Данный подход считается с середины XX века преобладающим, однако в действительности большинство математических работ не ставят задач перевести свои утверждения строго на язык теории множеств, а оперируют понятиями и фактами, установленными в некоторых областях математики. Таким образом, если в теории множеств будет обнаружено противоречие, это не повлечёт за собой обесценивание большинства результатов.

Логицизм Править

Основная статья: Логицизм

Данный подход предполагает строгую типизацию математических объектов. Многие парадоксы, избегаемые в теории множеств лишь путём специальных уловок, оказываются невозможными в принципе.

Формализм Править

Основная статья: Формализм (математика)

Данный подход предполагает изучение формальных систем на основе классической логики.

Интуиционизм Править

Основная статья: Интуиционизм

Интуиционизм предполагает в основании математики интуиционистскую логику, более ограниченную в средствах доказательства (но, как считается, и более надёжную). Интуиционизм отвергает доказательство от противного, многие неконструктивные доказательства становятся невозможными, а многие проблемы теории множеств — бессмысленными (неформализуемыми).

Конструктивная математика Править

Основная статья: Конструктивная математика

Конструктивная математика — близкое к интуиционизму течение в математике, изучающее конструктивные построения[прояснить]. Согласно критерию конструктивности — «существовать — значит быть построенным». Критерий конструктивности — более сильное требование, чем критерий непротиворечивости.

Сложные загадки на логику

Давайте попробуем разгадать 5 загадок на логику. Дети и взрослые могут размышлять над ответом вместе.

Загадка №5

Завязать можно, а развязать нельзя. Что это такое?

Справились? Если да – вы молодцы. А если что-то не получилось – приходите в Умназию и тренируйте ум с умом!

Умназия – образовательная онлайн-платформа для учеников начальной школы

На платформе ребенок сможет:
Развить логику и внимание на тренажере навыков, прокачать память и стать финансово грамотным!. У нас ребенку не будет скучно: умные алгоритмы подготовят для него индивидуальную программу, а в онлайн-тренажере он будет раскрывать тайны, получать достижения и становиться героем Умназии

У нас ребенку не будет скучно: умные алгоритмы подготовят для него индивидуальную программу, а в онлайн-тренажере он будет раскрывать тайны, получать достижения и становиться героем Умназии.

А для самых умных и мотивированных ребят у нас проводятся олимпиады по 4 предметам, которые готовят детей к будущим олимпиадам в школах. Приходите и развивайтесь вместе с нами!

Теперь приступим к более сложным заданиям. Включайте логику и начинайте!

Я – вода, и по воде плаваю. Кто я такая?

Загадка №7

Ползут 3 черепахи.1-я черепаха говорит: за мной ползут две черепахи.
2-я черепаха говорит: за мной ползёт одна черепаха и передо мной ползёт одна черепаха. А 3-я черепаха: передо мной ползут две черепахи, и за мной ползёт одна черепаха.

Как такое может быть?

Загадка №8

На ферме было 2 коня, 1 кролик, 1 щенок, 1 кошка, свинья и поросенок, корова и теленок, индюк и гусь.
Пришел Хозяин с собакой. Сколько на ферме стало ног?

Где впервые был обнаружен картофель?

Странный дождь порой идет: сотней струй он кверху бьет.

Почему логические загадки полезны для детей? Они развивают смекалку, учат работать с информацией, «прокачивают» логико-математический интеллект и делают ребенка более самостоятельным.

Помимо успехов в школе, о которых мы уже говорили, развитое логическое мышление способствует формированию уверенности в себе в процессе повседневной жизни.

>25 тысяч учеников уже решают авторские задачи в Умназии!

А теперь продолжим тренироваться, ведь долго без логики не протянешь!

Сколько яиц можно съесть натощак?

На сегодня это все — мы с вами славно потрудились.

Не хотите останавливаться на достигнутом? Регистрируйтесь в на нашей платформе и решайте тысячи задач в онлайн-режиме. Создавайте индивидуальный учебный план для вашего ребенка и развивайте пять навыков в удобное время.

Начните заниматься с ребенком уже сегодня!

Основные темы

Количество

Основной раздел, рассматривающий абстракцию количества — алгебра. Понятие «число» первоначально зародилось из арифметических представлений и относилось к натуральным числам. В дальнейшем оно, с помощью алгебры, было постепенно распространено на целые, рациональные, действительные, комплексные и другие числа.

1,2,…{\displaystyle 1,\;2,\;\ldots } Натуральные числа ,1,−1,…{\displaystyle 0,\;1,\;-1,\;\ldots } Целые числа 1,−1,12,23,,12,…{\displaystyle 1,\;-1,\;{\frac {1}{2}},\;{\frac {2}{3}},\;0{,}12,\;\ldots } Рациональные числа 1,−1,12,,12,π,2,…{\displaystyle 1,\;-1,\;{\frac {1}{2}},\;0{,}12,\;\pi ,\;{\sqrt {2}},\;\ldots } Вещественные числа
−1,12,,12,π,3i+2,eiπ3,…{\displaystyle -1,\;{\frac {1}{2}},\;0{,}12,\;\pi ,\;3i+2,\;e^{i\pi /3},\;\ldots }	1,i,j,k,πj−12k,…{\displaystyle 1,\;i,\;j,\;k,\;\pi j-{\frac {1}{2}}k,\;\dots }
Комплексные числа	Кватернионы

Числа — Натуральные числа — Целые числа — Рациональные числа — Иррациональные числа — Алгебраические числа — Трансцендентные числа — Вещественные числа — Комплексные числа — Гиперкомплексные числа — Кватернионы — Октонионы — Седенионы — Гиперреальные числа — Сюрреальные числа — p-адические числа — Математические постоянные — Названия чисел — Бесконечность — Базы

Преобразования

Явления преобразований и изменений в самом общем виде рассматривает анализ.

36÷9=4{\displaystyle 36\div 9=4}			∫1Sdμ=μ(S){\displaystyle \int 1_{S}\,d\mu =\mu (S)}
Арифметика	Дифференциальное и интегральное исчисление	Векторный анализ	Анализ
d2dx2y=ddxy+c{\displaystyle {\frac {d^{2}}{dx^{2}}}y={\frac {d}{dx}}y+c}
Дифференциальные уравнения	Динамические системы	Теория хаоса

Арифметика — Векторный анализ — Анализ — Теория меры — Дифференциальные уравнения — Динамические системы — Теория хаоса

Структуры

Теория множеств — Линейная алгебра — Общая алгебра (включает, в частности, теорию групп, универсальную алгебру, теорию категорий) — Алгебраическая геометрия — Теория чисел — Топология.

Пространственные отношения

Основы пространственных отношений рассматривает геометрия. Тригонометрия рассматривает свойства тригонометрических функций. Изучением геометрических объектов посредством математического анализа занимается дифференциальная геометрия. Свойства пространств, остающихся неизменными при непрерывных деформациях и само явление непрерывности изучает топология.

Геометрия	Тригонометрия	Дифференциальная геометрия	Топология	Фракталы	Теория меры

Геометрия — Тригонометрия — Алгебраическая геометрия — Топология — Дифференциальная геометрия — Алгебраическая топология — Линейная алгебра — Фракталы — Теория меры.

Дискретная математика

Дискретная математика включает средства исследования объектов, способных принимать только отдельные (дискретные) значения (то есть объектов, не способных изменяться плавно).

∀x(P(x)⇒P(x′)){\displaystyle \forall x(P(x)\Rightarrow P(x’))}
Математическая логика	Теория вычислимости	Криптография	Теория графов

Комбинаторика — Теория множеств — Теория решёток — Математическая логика — Теория вычислимости— Криптография — Теория функциональных систем — Теория графов — Теория алгоритмов — Логические исчисления
— Информатика.

Пьер де Ферма. 1601–1665

По профессии прославленный француз был юристом, а вот математическими исследованиями занимался в своё удовольствие. Но именно открытия в математике прославили Пьера Ферма.

Математик-самоучка блистал не только в области юриспруденции, но и был блестящим политологом. Стал основателем аналитической геометрии, внёс свой вклад в развитие математического анализа, теории чисел. Первым сделал классификацию кривых.

Пьер де Ферма вошёл в историю и как автор самой популярной арифметической загадки. Теорему Ферма не могли разгадать более 300 лет, и только в 1994 году она была доказана.

6

Этимология

Слово «математика» произошло от др.-греч. μάθημα, что означает изучение, знание, наука, и др.-греч. μαθηματικός, первоначально означающего восприимчивый, успевающий, позднее относящийся к изучению, впоследствии относящийся к математике. В частности, μαθηματικὴ τέχνη, на латыни ars mathematica, означает искусство математики. Термин др.-греч. μᾰθημᾰτικά в современном значении этого слова «математика» встречается уже в трудах Аристотеля (IV век до н. э.). По мнению Фасмера в русский язык слово пришло либо через польск. matematyka, либо через лат. mathematica.

В текстах на русском языке слово «математика» или «маѳематика» встречается, по крайней мере, с XVII века, например, у Николая Спафария в «Книге избранной вкратце о девяти мусах и о седмих свободных художествах» (1672 год).

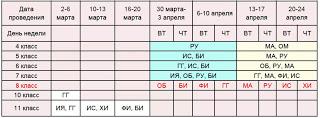
Кратко о ВПР

2020 год

Подготовка к ВПР в 8 классе

Дата проведения 14 апреля

Вынужденные каникулы уменьшили время на подготовку к ВПР.

Поэтому подборка заданий для самоподготовки с разбором заданий после прохождения теста .

Вам потребуется на выполнение теста 15 минут, потом 5-10 минут на разбор ошибок.

Задание 1 https://math8-vpr.sdamgia.ru/test?id=49213    (Действия с дробями)

Задание 2 https://math8-vpr.sdamgia.ru/test?id=49217   (Простейшие уравнения)

Задание 3 https://math8-vpr.sdamgia.ru/test?id=49223 (Простейшие текстовые задачи)

Задание 4 https://math8-vpr.sdamgia.ru/test?id=49228  (Числовые неравенства)

Задание 5  https://math8-vpr.sdamgia.ru/test?id=49232 (Формула линейной функции)

Повторение по теме «График функции линейной функции» Видеоурок

Март

Неравенства https://math-oge.sdamgia.ru/test?id=24055952

 Синус, косинус, тангенс https://math8-vpr.sdamgia.ru/test?id=28704

Февраль

Работа 1 https://math8-vpr.sdamgia.ru/test?id=3315 (алгебра)
Работа 2 https://math8-vpr.sdamgia.ru/test?id=6862 (алгебра)

Работа 3 https://math8-vpr.sdamgia.ru/test?id=6869 (алгебра)Работа 4 https://math8-vpr.sdamgia.ru/test?id=6879 (геометрия)

Подобие

 Треугольники и четырехугольники

23517409 Уравнения и выражения.

23191827(сбой)  (новое)Уравнения и задачи 

Подобие треугольников 

Теорема Пифагора. Подобие треугольников

Высказывания геометрические  Алгебраические дроби Теорема Пифагора. Площади Уравнения Вычисления Корни

Высказывания 1

Демоверсии

Описание проверочной работы по математике. 8 класс. 2020г.
Образец проверочной работы по математике. 8 класс. 2020г.

Книга для подготовкиТест 1

Читать далее: https://4ege.ru/vpr/57004-vpr-v-2018-2019-uchebnom-godu.html

До 18.04.2019 один вариантhttps://math7-vpr.sdamgia.ru/test?id=119633
До 16.04.2019 один вариантhttps://math7-vpr.sdamgia.ru/test?id=88215
До 09.04.2019 один вариантhttps://math7-vpr.sdamgia.ru/test?id=52865
До 02.04.2019 два варианта1)https://math7-vpr.sdamgia.ru/test?id=301282)https://math7-vpr.sdamgia.ru/test?id=30145
Все варианты, заданные ранее  (ниже), имеют неограниченный срок выполнения.

Готовимся на образовательном порталеhttps://math-oge.sdamgia.ru/

Можно кликнуть на номер задания, и, если вы зарегистрированы,то приступите к тесту. Номер Геометрия. Углы. Координатная плоскость Целые выражения Графики Геометрия. Длина отрезка Линейные уравнения. Анализ диаграмм Простейшие задачи на % Анализ таблиц Числа и вычисления Выше с датами и  с работающими ссылками все варианты!

7

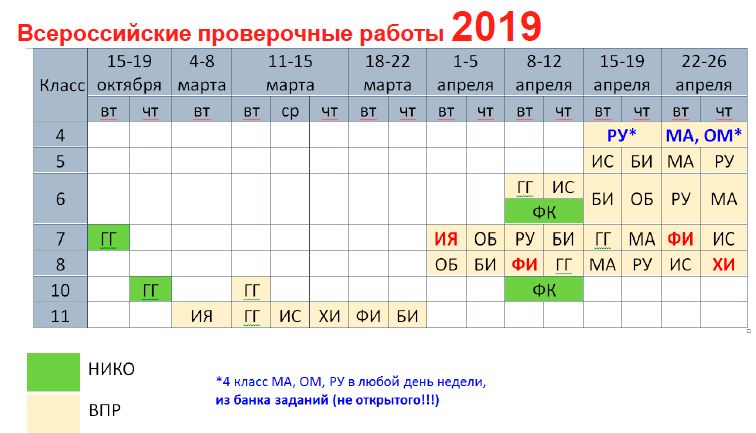
 5 класс

Алан Тьюринг

Известен: Криптоанализ загадки, Доказательства Тьюринга, премия Смита (1936)

Во время Второй мировой войны немецкая разведывательная сеть считалась почти непробиваемой. Многие союзные страны боялись, что, если они не смогут перехватить важные передачи нацистского верховного командования, они могут в конечном итоге проиграть войну.

Это был Алан Тьюринг, который благодаря своим беспрецедентным математическим и криптоаналитическим способностям значительно улучшил бомбу польского производства и разработал машину, способную быстрее декодировать Enigma.

После окончания войны Тьюринг присоединился к Национальной физической лаборатории (Великобритания), где он разработал автоматический вычислительный движок, один из самых ранних компьютеров с хранимой программой.

Позже в своей карьере он отвлек свое внимание на теоретическую биологию. Именно в это время он предсказал (математически) реакцию Белоусова – Жаботинского , которая позднее наблюдалась в 1960-х годах

Примечания

1. . www.classes.ru. Дата обращения 20 сентября 2017.
2. ↑ Бурбаки Н. Архитектура математики. Очерки по истории математики / Перевод И. Г. Башмаковой под ред. К. А. Рыбникова. М.: ИЛ, 1963. С. 32, 258.
3.  (недоступная ссылка). Сибирский открытый университет. Дата обращения 5 октября 2010.
4. Панов В. Ф. Математика древняя и юная. — Изд. 2-е, исправленное. — М.: МГТУ им. Баумана, 2006. — С. 581—582. — 648 с. — ISBN 5-7038-2890-2.
5.  . slovarus.info. Дата обращения 20 сентября 2017.
6. . classes.ru. Дата обращения 20 сентября 2017.
7. Словарь русского языка XI—XVII вв. Выпуск 9 / Гл. ред. Ф. П. Филин. — М.: Наука, 1982. — С. 41.
8. Декарт Р. Правила для руководства ума. М.-Л.: Соцэкгиз, 1936.
9. ↑ Математика / А. Н. Колмогоров // Большая Советская Энциклопедия / гл. ред. Б. А. Введенский. — 2-е изд. — М. : Государственное научное издательство «Большая Советская Энциклопедия», 1954. — Т. 26 : Магнитка — Медуза. — С. 464—483. — 300 000 экз.
10. «Чистая математика имеет своим объектом пространственные формы и количественные отношения действительного мира» в источнике: Маркс К., Энгельс Ф. Анти-Дюринг // Сочинения. — 2-е изд. — М.: Государственное издательство политической литературы, 1961. — Т. 20. — С. 37. — 130 000 экз.Оригинал цитаты (нем.) — «Die reine Mathematik hat zum Gegenstand die Raumformen und Quantitätsverhältnisse der wirklichen Welt» — в источнике:
11. Государственный образовательный стандарт высшего профессионального образования. Специальность 01.01.00. «Математика». Квалификация — Математик. Москва, 2000 (Составлено под руководством О. Б. Лупанова)
12. Я. С. Бугров, С. М. Никольский. Элементы линейной алгебры и аналитической геометрии. М.: Наука, 1988. С. 44.
13. Н. И. Кондаков. Логический словарь-справочник. М.: Наука, 1975. С. 259.
14. Г. И. Рузавин. О природе математического знания. — М., 1968.
15. . Wolfram MathWorld. Дата обращения 7 июля 2019.
16. . www.gsnti-norms.ru. Дата обращения 20 сентября 2017. (недоступная ссылка)

Как и почему требования отличаются — это НАУКА, а не ДАННЫЕ

Представьте веб-разработчика (или бизнес-аналитика). Он(а) ежедневно работает с большим объемом данных и информации, но не сталкивается со скрупулезным моделированием этих данных. Часто, для таких специалистов создают строгие временные рамки, и акцент делается на «использовании данных здесь и сейчас и затем работать дальше», а не на детальном научном исследовании этих данных. Нравится вам или нет, наука о данных всегда остается наукой (а не данными). Исходя из этого, определенные инструменты и методы являются незаменимыми. Многие из них являются критериями хорошего научного процесса:

• Моделирование процесса (физического или информативного) путем исследования основных динамик.
• Построение гипотез.
• Тщательная оценка качества источника данных.
• Количественная оценка неопределенности, касающейся данных и прогнозов.
• Развитие навыка идентификации скрытой характеристики в потоке информации.
• Четкое понимание ограниченности модели.
• (Иногда) понимание математического доказательства и всей абстрактной логики, на которой строится доказательство.

Такой вид обучения (большая его часть) развивает способность мыслить не одними числами, а абстрактными математическими категориями (а также их свойствами и взаимосвязями). Он преподносится как часть стандартной образовательной программы четырехлетнего обучения в университете. Не нужно иметь красный диплом ведущего университета, чтобы получить знания о такой математике. Но, к сожалению, мы не пользуемся этой доступностью 

И я говорю не о дифференциальном исчислении, которое проходят на первом курсе университета, а о чем-то более простом… Как цифра 2…

Что… Что еще за рациональное число?

Поняли, о чем я?

Этот этап сравним с осознанием того, что кажущаяся пустота вокруг нас заполнена воздухом.

Ещё раньше, в 1727 г., знаменитый математик Даниил Бернулли, работавший в то время в Петербургской академии наук, обратил внимание на студента этой академии Василия Евдокимовича Ададурова . В письме к известному математику Христиану Гольдбаху от 28 мая 1728 г

Бернулли отмечает значительные математические способности молодого человека и сообщает о сделанном Ададуровым открытии: сумма кубов последовательных натуральных чисел равна квадрату суммы их первых степеней: 13 + 23 +… + п3 = = (1 + 2 +… + п)2. Математические заслуги Ададурова засвидетельствованы включением статьи о нём (с портретом, выполненным в технике силуэта) в биографический раздел однотомного «Математического энциклопедического словаря» (М., 1988). А из статьи «Ададуров» в первом томе «Нового энциклопедического словаря» Брокгауза и Ефрона мы узнаём, что Ададуровым написано несколько сочинений по русскому языку и, более того, что «в 1744 г. ему было поручено преподавать русский язык принцессе Софии, т. е. будущей императрице Екатерине II». Последующие изыскания (они были проведены братом автора этих строк Борисом Андреевичем Успенским) показали, что Ададуров является автором первой русской грамматики на русском же языке, составление каковой следует рассматривать как большое событие. Ведь важнейший этап в языковом сознании носителей какого бы то ни было языка — появление первой грамматики этого языка на том же самом языке; этот этап сравним с осознанием того, что кажущаяся пустота вокруг нас заполнена воздухом. Прибавим ещё, что с 1762 по 1778 г. Ададуров был куратором Московского университета — вторым после основавшего университет И. И. Шувалова.

Итак, даже если согласиться с традиционной классификацией наук, отсюда ещё не следует с неизбежностью аналогичная классификация учёных или учащихся. Приведённые факты показывают, что математик и гуманитарий способны уживаться в одном лице. Здесь предвидятся два возражения. Прежде всего нам справедливо укажут, что Ададуров, Барсов, Колмогоров были выдающимися личностями, в то время как любые рекомендации должны быть рассчитаны на массовую аудиторию. На это мы ответим, что образцом для подражания — даже массового подражания — как раз и должны быть выдающиеся личности и что примеры Ададурова, Барсова, Колмогорова призваны вдохновлять. Далее нам укажут, опять-таки справедливо, что отнюдь не всем гуманитариям и отнюдь не всем математикам суждено заниматься научной работой, это и невозможно, и не должно. Ну что ж, ответим мы, примеры из жизни больших учёных выбраны просто потому, что история нам их сохранила; сочетать же математический и гуманитарный подход к окружающему миру стоит даже тем гуманитариям и математикам, которые не собираются посвятить себя высокой науке, и это вполне посильная для них задача. 

Подписи к слайдам:

Слайд 1

Ж ЕНЩИНЫ-ВЕЛИКИЕ МАТЕМАТИКИ Презентацию подготовила ученица 7 «г» класса Айрапетова Виктория.

Слайд 2

Портреты женщин-математиков

Слайд 3

Великие Русские женщины- математики 1. Софья Васильевна Ковалевская 2. Ольга Александровна Ладыжевская 3. Ольга Арсентьевна Олейник 4. Надежда Николаевна Гернет 5. Пелагея Яковлевна Кочина 6. Людмила Всеволодовна Келдыш 7. Нина Карловна Бари

Слайд 4

С офи Ж ермен (1 апреля 1776-27 июня 1831) Ф ранцузский математик, философ и механик . Софи Жермен вывела несколько формул, названных её именем . Доказала так называемый «Первый случай» Великой теоремы Ферма для простых чисел. Софи становится первой женщиной, получившей право участия в заседаниях Парижской Академии наук. На рисунке изображена Софи Жермен в 14 лет.

Слайд 5

с офья в асильевна к овалевская ( 3 января 1850 , Москва — 29 января 1891 ) Р усский математик и механик, с 1889 года иностранный член-корреспондент Петербургской Академии наук . Первая в России и в Северной Европе женщина-профессор и первая в мире женщина-профессор математики. Автор повести «Нигилистка» и «Воспоминаний детства».

Слайд 6

а да лавлейс ( 10 декабря 1815 — 27 ноября 1852 ) Англичанка-математик. Родилась в Великобритании в Лондоне, умерла там же. Известна прежде всего созданием описания вычислительной машины, проект которой был разработан Чарльзом Бэббиджем. Ввела в употребление термины «цикл» и «рабочая ячейка», считается первым программистом.

Слайд 7

н иколь- р ейн л епот ( 5 января 1723 , — 6 декабря 1788 ) Первая французская женщина-математик и астроном . Николь-Рейн Лепот родилась 5 января 1723 годав Люксембургском дворце в Париже умерла во Франции. Мадам Лепот участвовала в расчете орбиты кометы Галлея, была составительницей эфемерид Солнца , Луны и планет. Работы Николь-Рейн Этабль де ла Бриер публиковались в изданиях Парижской академии. В честь мадам Лепот была первоначально названа гортензия (» потией «).

Слайд 8

Гипатия ( Ипатия ) Александрийская ( 370 н.э. – 415 н.э.) Женщина-учёный греческого происхождения, философ, математик, астроном. Гипатия , по описанию историков, была женщиной необыкновенной красоты и большого ума . Отец Гипатии — Теон Александрийский, крупный ученый-математик. Гипатия , помимо математики, занималась также философией и астрономией.

Слайд 9

м ария Г аэтана А ньези ( 16 мая 1718 — 9 января 1799 ) Итальянский математик и филантроп . Её отец был профессором математики, он с детства поддерживал математические способности дочери и позаботился о хорошем образовании Марии Гаэтаны . В 1748 году она опубликовала свою работу Instituzioni analitiche («Основы анализа »). Она имела также достижения в дифференциальном исчислении. Мария Гаэта умерла 9 января 1799 года в 8о лет .

Слайд 10

Э мили Д ю Ш атле ( 17 декабря 1706 — 10 сентября 1749 ) ф ранцузский математик и физик . Габриэль-Эмилия ле Тоннелье де Бретейль родилась в Париже 17 декабря 1706. Она самостоятельно изучила математику, физику и языки. Муза и возлюбленная Вольтера . Доказала, что кинетическая энергия тела – функция квадрата его скорости.

Слайд 11

н адежда н иколаевна г ернет ( 18 апреля 1877 — 1943 , Ленинград ) Р усский и советский математик и педагог, ученица Д. Гильберта. Профессор Высших женских курсов в Петербурге. Работала в области вариационного исчисления . Провела исследование радиуса круга сходимости ряда Лагранжа.

Слайд 12

П елагея Я ковлевна К очина ( 1 мая 1899 — 3 июля 1999 ) Советский физик-гидродинамик, академик Академии В 1921 году окончила физико-математический факультет Петроградского университета наук СССР . В 1940 году защитила диссертацию на соискание учёной степени доктора физико-математических наук. 4 декабря 1946 года была избрана членом-корреспондентом Академии наук СССР по специальности «гидродинамика».

Слайд 13

СПАСИБО ЗА ВНИМАНИЕ !!!

Софи Жермен (1776—1831)

Ей было только 13, когда она развила активный интерес к математике; ответственность за это можно возложить на Французскую революцию. Поскольку вокруг ее дома бушевала борьба, Жермен не могла исследовать улицы Парижа, вместо этого она исследовала библиотеку своего отца, самостоятельно изучая латинский и греческий, а также читала уважаемые математические труды.

Так как возможности получения образования у женщин были ограничены, Жермен тайно училась в Политехнической школе, используя имя зарегистрированного студента. Это работало до тех пор, пока учителя не заметили необъяснимое улучшение математических навыков студента.

Жермен известна, прежде всего, своей работой над Последней теоремой Ферма, которая, как полагали в то время, была одной из самых сложных математических задач.

«И я решил уйти в науку, в которой для окончательного вывода достаточно одного доказательства».

Первая научная работа великого математика Андрея Николаевича Колмогорова была посвящена отнюдь не математике, а истории. В начале 1920-х гг., будучи семнадцатилетним студентом математического отделения Московского университета, он доложил свою работу на семинаре известного московского историка Сергея Владимировича Бахрушина. Она была опубликована посмертно и чрезвычайно высоко оценена специалистами — в частности, руководителем Новгородской археологической экспедиции Валентином Лаврентьевичем Яниным. Выступая на вечере памяти Колмогорова, состоявшемся в Московском доме учёных 15 декабря 1989 г., он так охарактеризовал историческое исследование Колмогорова: «Эта юношеская работа в русле исторической науки занимает место, до которого её развитие ещё не докатилось. Будучи опубликованной, она окажется впереди всей исторической науки».

А в предисловии к вышеназванному посмертному изданию исторических рукописей Колмогорова В. Л. Янин писал: «Некоторые наблюдения А. Н. Колмогорова способны пролить свет на источники, обнаруженные много десятилетий спустя после того, как он вёл своё юношеское исследование». И там же: Андрей Николаевич сам неоднократно рассказывал своим ученикам о конце своей «карьеры историка». Когда работа была доложена им в семинаре, руководитель семинара профессор С.В. Бахрушин, одобрив результаты, заметил, однако, что выводы молодого исследователя не могут претендовать на окончательность, так как «в исторической науке каждый вывод должен быть снабжён несколькими доказательствами» (!). Впоследствии, рассказывая об этом, Андрей Николаевич добавлял: «И я решил уйти в науку, в которой для окончательного вывода достаточно одного доказательства». История потеряла гениального исследователя, математика приобрела его.

Двадцать шестого апреля (по старому стилю, а по новому — 7 мая) 1755 г. состоялось торжественное открытие Московского университета. После молебна были сказаны четыре речи. Первая из них — и притом единственная прозвучавшая на русском языке — называлась «О пользе учреждения Московского университета». Произнёс её Антон Алексеевич Барсов . Неудивительно, что в 1761 г. он был назначен профессором (в современных терминах — заведующим) на кафедру красноречия; вступление в эту должность ознаменовалось его публичной лекцией «О употреблении красноречия в Российской империи», произнесённой 31 января (11 февраля) 1761 г. Чем же занимался Барсов до того? Преподавал математику — именно с Барсова, в феврале 1755 г. специально для этой цели переведённого из Петербурга в Москву, и началось преподавание математики в Московском университете! Впоследствии Барсов прославился трудами по русской грамматике; ему же принадлежит и ряд предложений по русской орфографии, тогда отвергнутых и принятых лишь в XX в. К сожалению, портрет А. А. Барсова не сохранился.