Пространство — это.. понятие и виды пространства
Содержание:
Математика
Математическая дисциплина рассматривает пространство через призму логики, однако и она не обходится без участия философии. Основной проблемой здесь является соотношение реальной действительности с миром абстрактных конструкций, которые свойственны математике. Как и везде, эта наука пытается объяснить явление при помощи конкретных расчетов, поэтому для неё пространство – это множество, обладающее структурой.
Математика определяет его как среду, в которой осуществляются различные объекты и предметы. Все сводится к элементарной геометрии, где фигуры (точки) существуют в одной или нескольких плоскостях. В связи с этим появилась необходимость как-то охарактеризовать, измерить пространство. Для этого математиками используются такие характеристики, как длина, масса, скорость, время, объем и т. п.
В математической науке принято выделять такие виды пространства: Евклидово, Афинное, Гильбертово, Векторное, Вероятностное, двухмерное, трехмерное и даже восьмимерное. Всего их в математике выделяется не менее 22 типов.
Философское понятие
Прежде чем давать характеристику пространству, надо понимать, что этот термин далеко не однозначен. Понятие пространства фигурирует в математике, физике, географии, философии, религии и фантастике. Различные дисциплины понимают его по-разному и находят свои трактовки в зависимости от поставленных задач. Самым простым и приземленным определением является следующее: пространство – это место, в котором что-либо вмещается; расстояние между различными предметами.

Философия рассматривает его как одну из фундаментальных категорий, неотъемлемо связанную со временем. Это отношение между различными объектами, их взаимоположение, связь в конкретный период времени. Оно является определенностью бытия, характеризующей способ существования материи.
Согласно философии, пространство обладает конкретными свойствами, а именно протяженностью, разнородностью, структурностью, анизотропностью, непрерывностью. Оно постоянно взаимодействует со временем, образуя так называемый хронотоп.
Единицы площади и объема
Для традиционных (гиперкубических) единиц площади и объема известны формулы объема \(V_N(R)\) и поверхности \(S_N(R)\) гиперсферы:
\
\
\
| Мерность N | Фигура | Объем | Поверхность | Углы |
|---|---|---|---|---|
| 1 | Отрезок | \ | два направления | |
| 2 | Круг | \ | \ | \(2\pi\) радиан |
| 3 | Шар | \ | \ | \(4\pi\) стерадиан |
| 4 | 4D-гиперсфера | \ | \ |
Коэффициент \(C(N)\) имеет также определение через гамма-функцию Эйлера с вещественным аргументом:
\[C(N)=\frac{\pi^{N/2}}{\Gamma(N/2+1)},\;\;\;\;\;\Gamma(x)=\int_0^{+\infty}{t^{x-1}e^{-t}\mathrm{d}t}\]
Применение гиперсферических единиц для объема и площади изменяет интегральное исчисление и формулы объема и поверхности:
\
\
Величина \(X(N)\) ищется из ряда условий:
- Длина окружности или «поверхность круга» в этом случае также равна \(2\pi R\).
- Отношение площади поверхности сферы к площади круга того же радиуса равно \(4\).
- Отношение площади поверхности 4D-гиперсферы к площади сферы того же радиуса равно \(3\pi⁄2\).
Этим условиям удовлетворяет такое решение:
\
| Мерность | Фигура | Объем | Поверхность |
|---|---|---|---|
| 1 | Отрезок | \ | |
| 2 | Круг | \ | \ |
| 3 | Шар | \ | \ |
| 4 | 4D-гиперсфера | \ | \ |
| \(D\) – диаметр. |
Объем эллипсоида в гиперсферических единицах – произведение его диаметров.
При кратном интегрировании в гиперсферических единицах, необходимо делать поправки:
- Двойной интеграл. Отношение площади квадрата к площади вписанного в него круга, равное \(4/\pi\).
- Тройной интеграл. Отношение объема куба к объему вписанного в него шара, равное \(6/\pi\).
Теория времени Митрофана Аксёнова
В конце XIX века русский философ Митрофан Аксёнов выдвинул теорию, предвосхитившую учение А. Эйнштейна и Г. Минковского о пространстве-времени. Теория, названная автором трансцендентально-кинетической теорией времени, была изложена им в четырёх трактатах, вышедших в период с 1896 по 1918 гг. По учению Аксёнова, мир протяжён не в трёх, а в четырёх измерениях, а время есть движение нашего «я» в четвёртом измерении.
Аксёнов считал абсурдным общепринятое мнение, согласно которому прошлого и будущего не существует, а настоящее представляет собой исчезающе малое, непрестанно обращающееся в ничто мгновение. Этому взгляду он противопоставил своё убеждение, согласно которому прошлое и будущее столь же реальны, сколь и настоящее. Прошлое не исчезает, а лишь проходит, по буквальному смыслу слова, мимо нас, равно как и будущее не возникает, а существует от века. Иллюзия, будто прошлого и будущего не существует, происходит оттого, что мы не можем совершать во времени, как в пространстве, произвольных движений; будь у нас такая возможность, мы бы легко убедились в своей ошибке.
Наше «я», движущееся в четвёртом измерении, Аксёнов называл «воспринимающим началом», сознанием или духом; его движение в четырёхмерном мире не является предметом нашего опыта и потому есть движение трансцендентальное. Вещи, данные нам в ощущениях, суть не реальные объекты, а лишь трёхмерные срезы, сечения или проекции подлинных четырёхмерных вещей, подобные тем теням на стене пещеры, о которых писал Платон. В подлинном, четырёхмерном мире нет ни возникновения, ни уничтожения, ни движения, ни изменения, но всё это — иллюзии, порождённые трансцендентальным движением нашего «я». Иллюзорны также понятия действия, причинности и свободы воли, порождённые перенесением на внешние объекты внутренних свойств нашего «я». В мире царит строжайший детерминизм, обусловленный геометрическим строением четырёхмерных объектов, а само движение нашего «я» подобно движению пассажира в несущемся по рельсам никем не управляемом поезде.
В то же время, полагал философ, мы обладали свободой воли до своего рождения, и наш жизненный путь является результатом нашего трансцендентального выбора. Наше «я» сверхвременно, неуничтожимо и бессмертно, оно существовало до нашего рождения и будет существовать после нашей смерти. Оно не зависит от времени, ибо само чертит линию времени своим движением, и предположить его уничтожение — значит предположить, что рука, чертящая линию, прекращает существовать с прекращением этого черчения.
В ролях
- Основной состав
- Стивен Стрейт — Джеймс «Джим» Холден. Персонажу Стрейта нравится его простая жизнь и минимум ответственности, несмотря на то, что работа в космосе сопряжена с риском — это лучший способ исчезнуть из виду. Холден — второй помощник капитана на борту корабля «Кентербери». Один из пяти выживших, который на протяжении шести лет отказывался от всякого повышения. Отвечает на сигнал бедствия, посланный с корабля «Скопули» Джульеттой Мао. Любит кофе. Принимает химический коктейль под названием «Сок», чтобы выжить в космосе во время перелётов. Стивен Стрейт считает, что у сериала прекрасные сценаристы, которые адаптируют книги, отличный режиссёр, и есть шанс создать что-то, чем вся съёмочная группа будет гордиться.
- Доминик Типпер — Наоми Нагата, инженер на «Кентербери». Родилась на Церере, не видела солнечного света, дождя, не вдыхала свежий воздух. Она человек из рабочего класса. Доминик считает свою героиню прекрасным лжецом, которая, находясь под давлением, всё же справляется с ситуацией. После взрыва корабля и повреждения шаттла чинит радиосвязь, чтобы позвать на помощь, в результате сигнал принимает марсианский флагман «Доннаджер». Её подозревают в членстве в «СВП».
- Кэс Анвар — Алекс Камаль, пилот на «Кентербери». Бывший офицер марсианского флота, ушедший в почётную отставку.
- Уэс Чэтэм — Эймос Бартон, механик на «Кентербери». Жёсткий и практичный человек с тёмным прошлым, испытывающий чувства к Нагате.
- Томас Джейн — детектив Джозеф «Джо» Алоис Миллер, полицейский на Церере. Персонаж Джейна родился и вырос в космосе, рано лишившись родителей, погибших при строительстве станции. Миллер вырос «на улице», скитаясь, он научился выживать. Берёт взятки, не притворяясь, что его это смущает, он знает, как устроена жизнь, ему плевать на общество, он вырос вне его. Миллер сам трактует закон так, как считает нужным, потому что понимает, что он не застрял на астероиде в космосе, он будто шериф в старом «вестерне». Ради этой роли актёру пришлось сбросить вес, так как по сюжету действие разворачивается на астероидах, в условиях низкой гравитации, из-за этого люди вырастают худыми и высокими. По мнению актёра, его герой все время тепло одет лишь потому, что в космосе довольно холодно, и он мог бы себе что-то отморозить и потерять. Джейн отзывался о своём персонаже, как о настоящей «заднице», но все же надеется, что зрителям он понравится.
- Шохре Агдашлу — Крисьен Авасарала, помощник заместителя Генерального секретаря ООН по административным делам, ведущая расследование обстоятельств гибели судов.
- — Садавир Эрринрайт, заместитель Генерального секретаря ООН по административным делам.
- Фрэнки Адамс — Роберта «Бобби» Дрейпер, комендор-сержант марсианской пехоты.
- Второстепенный состав
- Чад Коулмэн — Фред Джонсон. «Мясник станции Андерсон», руководитель ячейки СВП и начальник станции «Тихо».
- — Пракс. Ботаник с Ганимеда, разыскивающий похищенную дочь.
- — Камина Драммер. Помощница Фреда Дожонсона, позднее капитан «Бегемота».
- Элизабет Митчелл — преподобный доктор Анна Воловодова. Земной и европеанский пастор методизма.
- Флоренс Фэйвр — Джульетта «Жюли» Андромеда Мао. Разыскивается детективом Миллером, отправляет сигнал бедствия, на который откликается Джеймс Холден.
- Афена Карканис — Октавия Масс, 7 серий.
- Кристен Хагер — Ада Нигаард, 2 серии.
- Пауло Костанцо — 1 серия.
- Джей Эрнандес — Дмитрий Хэвлок, напарник Джозефа Миллера на Церере.
- Элайс Туфексис — Кензо, шпион со станции «Тихо».
- Грег Брайк — лейтенант марсианского корабля «Доннеджер».
- Джонатан Бэнкс — старпом «Кентербери», 1-я серия.
- Джаред Харрис — Андерсон Доус, лидер СВП.
- Франсуа Шо — Жюль-Пьер Мао.
- Джефф Сеймур — Коршунов, министр обороны Марса.
Примечания
- Физическое пространство — это уточняющий термин, используемый для разграничения этого понятия как от более абстрактного (обозначаемого в этой оппозиции как абстрактное пространство), так и для различения реального пространства от слишком упрощенных его математических моделей.
- Тут имеется в виду трёхмерное «обычное пространство», то есть пространство в понимании (1), как описано в начале статьи. В традиционных рамках теории относительности стандартным является именно такое употребление термина (а для четырёхмерного пространства Минковского или четырёхмерного псевдориманова многообразия общей теории относительности используется соответственно термин пространство-время). Однако в более новых работах, особенно если это не может вызвать путаницы, термин пространство употребляют и в отношении пространства-времени в целом. Например, если говорят о пространстве размерности 3+1, имеется в виду именно пространство-время (а представление размерности в виде суммы обозначает сигнатуру метрики, как раз и определяющую количество пространственных и временных координат этого пространства; во многих теориях количество пространственных координат отличается от трёх; существуют и теории с несколькими временными координатами, но последние очень редки). Аналогично говорят «пространство Минковского», «пространство Шварцшильда», «пространство Керра» и т. д.
- Возможность выбора разных систем пространственно-временных координат и перехода от одной такой системы координат к другой, аналогичен возможности выбора разных (с разным направлением осей) систем декартовых координат в обычном трёхмерном пространстве, причём от одной такой системы координат можно перейти к другой поворотом осей и соответствующим преобразованием самих координат — чисел, характеризующих положение точки в пространстве относительно данных конкретных декартовых осей. Однако следует заметить, что преобразования Лоренца, служащие аналогом поворотов для пространства-времени, не допускают непрерывного поворота оси времени до произвольного направления, например, ось времени нельзя повернуть до противоположного направления и даже до перпендикулярного (последнему соответствовало бы движение системы отсчета со скоростью света).
Космическое пространство
Понимание пространства различными науками не ограничивается пределами Земли. Учитывая, что физика допускает его бесконечность, можно говорить о значительном расширении границ, например до Вселенной (главная система, совокупность всего, что есть в мире).

Незаполненные никакими телами участки между объектами во Вселенной – это космическое пространство. Оно находится за пределами небесных тел, а значит, и вне Земли и её атмосферы. Однако «космическая пустота» все же чем-то заполнена: она состоит из частиц водорода, межзвездного вещества и электромагнитного излучения.
Казалось бы, если есть объекты, которые не входят в пространство, то можно четко определить его начало. На самом деле сделать это сложно, так как земная атмосфера разрежается постепенно, и границы её значительно размываются. Для разделения атмосферы и космоса международное сообщество приняло условную высоту в 100 километров. Хотя многие астрономы уверены, что космос начинается только на 120 километре от поверхности Земли.
Атомы пространства-времени
Тепло — это случайное движение микроскопических частиц, вроде молекул газа. Поскольку черные дыры могут нагреваться и остывать, было бы разумно предположить, что они состоят из частей — или, если в общем, из микроскопической структуры. И поскольку черная дыра — это просто пустое пространство (согласно ОТО, падающая в черную дыру материя проходит через горизонт событий, не останавливаясь), части черной дыры должны быть частями самого пространства. И под обманчивой простотой плоского пустого пространства скрывается колоссальная сложность.
Даже теории, которые должны были сохранять традиционное представление о пространстве-времени, пришли к выводам, что что-то прячется под этой гладкой поверхностью. Например, в конце 1970-х годов Стивен Вайнберг, сейчас работающий в Техасском университете в Остине, попытался описать гравитацию так же, как описывают другие силы природы. И выяснил, что пространство-время радикально модифицировано в своих мельчайших масштабах.
Физики изначально визуализировали микроскопическое пространство как мозаику из небольших кусочков пространства. Если увеличить их до планковских масштабах, неизмеримо малых размеров в 10-35 метра, ученые считают, что можно увидеть нечто вроде шахматной доски. А может и нет. С одной стороны, такая сеть линий шахматного пространства будет предпочитать одни направления другим, создавая асимметрии, которые противоречат специальной теории относительности. Например, свет разных цветов будет двигаться с разной скоростью — как в стеклянной призме, которая разбивает свет на составляющие цвета. И хотя проявления на малых масштабах будет весьма трудно заметить, нарушения ОТО будут откровенно очевидными.
Термодинамика черных дыр ставит под сомнение картину пространства в виде простой мозаики. Измеряя тепловое поведение любой системы, вы можете сосчитать ее части, по крайней мере в принципе. Сбросьте энергию и посмотрите на термометр. Если столбик взлетел, энергия должна распространяться на сравнительно немного молекул. Фактически, вы измеряете энтропию системы, которая представляет собой ее микроскопическую сложность.
Если проделать это с обычным веществом, количество молекул увеличивается вместе с объемом материала. Так, во всяком случае, должно быть: если увеличить радиус пляжного мяча в 10 раз, внутри него поместится в 1000 раз больше молекул. Но если увеличить радиус черной дыры в 10 раз, число молекул в ней умножится всего в 100 раз. Число молекул, из которых она состоит, должно быть пропорциональным не ее объему, а площади поверхности. Черная дыра может казаться трехмерной, но ведет себя как двумерный объект.
Этот странный эффект получил название голографического принципа, потому что напоминает голограмму, которая видится нам как трехмерный объект, а при ближайшем рассмотрении оказывается изображением, произведенным двумерной пленкой. Если голографический принцип учитывает микроскопические составляющие пространства и его содержимого — что физики допускают, хоть и не все — для создания пространства будет недостаточно простого сопряжения мельчайших его кусочков.
15.2 Неограниченное архитектурное пространство
В организации неограниченного архитектурного пространства участвуют: основной (главный) архитектурный объём или группа объемов, вокруг которых организуется пространство, и поверхность основания, на которой находится пространственная композиция.
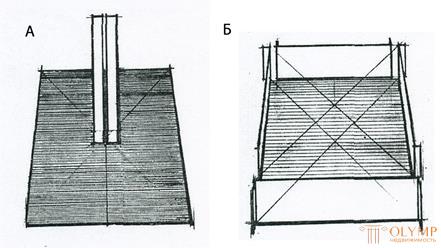
Рисунок 59: А – схема, неограниченное пространство; Б – схема, ограниченное пространство
Положение основного элемента в неограниченном пространстве определяется по отношению к осям координат, относительно которых он может занимать основную или промежуточную по значимости позицию, т. е. быть в горизонтальном, вертикальном или наклонном положении.
Для поверхности основания в неограниченном пространстве характерным является её форма и положение в пространстве.
Наиболее распространённая форма поверхности основания – условно плоская (горизонтальная) и условно выпуклая (сложная).
Ощущение организованности неограниченного пространства увеличивается по направлению к основному архитектурному объёму. Поэтому динамика, напряжённость композиционной сферы зависит прежде всего от активности решения архитектурного элемента и взаимодействия его с поверхностью основания.
Главный композиционный элемент несёт в себе одновременно функции центра и доминанты пространственной композиции, так как является, по существу, единственной вещественной основой для этого вида организации архитектурной формы. Актуальность композиционного решения основного архитектурного элемента зависит от его формы, величины, массивности, положения в пространстве, пластического выявления. Естественно, что от всех перечисленных факторов в значительной степени зависит взаимодействие основного архитектурного элемента с окружающим его пространством, выразительность всего композиционного построения (пример: Эйфелева башня в Париже. Развитость этой доминанты по вертикали создаёт динамику не только в ней самой, но и влияет на восприятие окружающего пространства).
Поверхность основания в неограниченном пространстве является важнейшим элементом этого вида композиции. В зависимости от характера поверхности и взаимодействия с основным элементом она может определять характер пространственной композиции. При плоской горизонтальной поверхности основания наиболее распространённые решения основных элементов лежат в пределах, заключённых между решением, когда элемент развит по вертикали и противопоставляется горизонтальной поверхности основания, и другим случаем – когда элемент приближается к равноразмерной форме.
Таким образом, характер неограниченного архитектурного пространства зависит от особенностей основного композиционного элемента, характера поверхности основания и взаимодействия этих элементов композиции.
Представление времени в литературе
В литературе понятие определяется, как временное построение, передаваемое разными ракурсами перевоплощения, действия и понимания через литературные произведения, как разновидности искусства. Искусство выступает информационным средством.
В литературном произведении действие происходит между тремя субъектами – автор, главный герой, читатель. Из этого следует, что текст связан с временем следующими координатами:
- Реальный период создания – век, дата, протяженность процесса создания;
- Период использования – измерение функционирования слова в конкретном произведении (пергаменте, папирусе, книге, информационном источнике);
- Период восприятия читателем.
Время нахождения литературного издания никак не связано с временем, которое оно отображает, так как произведение есть объект эстетического осмысления. Он показывает временное расстояние: изображение реальности, как целостной картины; передача условий существования предмета; отображение прошедшего, настоящего, будущего; изменения одного и того же художественного образа. Объект не эстетического осмысления не передает динамику.
Существует четвертая координата – художественное время (внешний событийный фон художественной реалии произведения). Фабульное (возможность действий, реакции, жесты персонажа) выступает его частью. Оно необходимо для конкретной датировки действий, ощущения реальности созданной действительности.
На самом деле для автора понятие выступает способом изображения главного персонажа жизни.
Вниз по черной дыре
Обычный магнитик на холодильнике прекрасно иллюстрирует проблему, с которой столкнулись физики. Он может приколоть бумажку и сопротивляться гравитации всей Земли. Гравитация слабее магнетизма или другой электрической или ядерной силы. Какие бы квантовые эффекты за ней ни стояли, они будут слабее. Единственное осязаемое доказательство того, что эти процессы вообще происходят, это пестрая картина материи в самой ранней Вселенной — которая, как полагают, была нарисована квантовыми флуктуациями гравитационного поля.
Черные дыры — лучший способ проверить квантовую гравитацию. «Это самое подходящее, что можно найти для экспериментов», говорит Тед Джейкобсон из Университета Мэриленда, Колледж-Парк. Он и другие теоретики изучают черные дыры как теоретические точки опоры. Что происходит, когда берутся уравнения, которые идеально работают в лабораторных условиях, и помещаются в самые экстремальные ситуации из мыслимых? Не появится ли какой-нибудь едва заметной огрехи?
Общая теория относительно предсказывает, что вещество, падающее в черную дыру, бесконечно сжимается по мере приближения к центру — математическому тупичку под названием сингулярность. Теоретики не могут вообразить траекторию объекта за пределами сингулярности; все линии сходятся в ней. Даже говорить о ней, как о месте, проблематично, потому что само пространство-время, определяющее местоположенрие сингулярности, прекращает существовать. Ученые надеются, что квантовая теория может предоставить нам микроскоп, который позволит рассмотреть эту бесконечно малую точку бесконечной плотности и понять, что происходит с попадающей в нее материей.
На границе черной дыры вещество еще не настолько сдавлено, гравитация слабее и, насколько нам известно, все законы физики должны работать. И тем больше обескураживает тот факт, что они не работают. Черная дыра ограничена горизонтом событий, точкой невозврата: вещество, преодолевающее горизонт событий, уже не вернется. Спуск необратим. Это проблема, потому что все известные законы фундаментальной физики, включая квантово-механические, обратимы. По крайней мере, в принципе, в теории, вы должны иметь возможность обратить движение и восстановить все частицы, которые у вас были.
С похожей головоломкой физики столкнулись в конце 1800-х, когда рассматривали математику «черного тела», идеализированного как полость, заполненная электромагнитным излучением. Теория электромагнетизма Джеймса Клерка Максвелла предсказывала, что такой объект будет поглощать все излучение, которое на него падает, и никогда не придет в равновесие с окружающей материей. «Он может поглотить бесконечное количество тепла от резервуара, который поддерживается при постоянной температуре», объясняет Рафаэль Соркин из Института теоретической физики Периметра в Онтарио. С тепловой точки зрения у него будет температура абсолютного нуля. Этот вывод противоречит наблюдениям настоящих черных тел (таких как печь). Продолжая работу над теорией Макса Планка, Эйнштейн показал, что черное тело может достичь теплового равновесия, если энергия излучения будет поступать в дискретных единицах, или квантах.
Физики-теоретики почти полвека пытались достичь подобного решения для черных дыр. Покойный Стивен Хокинг из Кембриджского университета предпринял важный шаг в середине 70-х, применив квантовую теорию к полю излучения вокруг черных дыр и показав, что у них ненулевая температура. Следовательно, они могут не только поглощать, но и излучать энергию. Хотя его анализ ввернул черные дыры в область термодинамики, он также усугубил проблему необратимости. Исходящее излучение испускается на границе черной дыры и не переносит информацию из недр. Это случайная тепловая энергия. Если обратить процесс и скормить эту энергию черной дыре, ничего не всплывет: вы просто получите еще больше тепла. И невозможно вообразить, что в черной дыре что-то осталось, просто в ловушке, потому что по мере того, как черная дыра испускает излучение, она сокращается и, согласно анализу Хокинга, в конечном итоге исчезает.
Эта проблема получила название информационного парадокса, поскольку черная дыра разрушает информацию о попавших в нее частицах, которые вы могли бы попытаться восстановить. Если физика черных дыр действительно необратимо, что-то должно выносить информацию обратно, и нашу концепцию пространства-времени, возможно, придется изменить, чтобы вписать этот факт.
Презентизм, этернализм, растущий блок
- Основные статьи: , Этернализм, Растущий блок Вселенной
В соответствии с теорией , объекты реально существуют только в настоящем. Настоящее — это единственная реальность, с которой мы имеем дело и мы не можем говорить, что, например, А. С. Пушкин существует, потому что в настоящее время его уже нет в живых. В противоположность этому, теория этернализма утверждает, что измерение времени по своим свойствам аналогично остальным трем пространственным измерениям. Поэтому все объекты — будь то существовавшие в прошлом, существующие сейчас или же те, которые будут существовать в будущем — могут быть обозначены как реально существующие совершенно так же, как и непосредственно воспринимаемые объекты настоящего. В соответствии с теорией этернализма, А. С. Пушкин, в действительности, существует, хотя необходимо использовать особые языковые конструкции, когда говорят о ком-то, кто существует в отдаленном времени — совершенно так же, как мы особо подчеркиваем, когда говорим о чём-то, что находится очень далеко (сами слова и выражения «вблизи», «вдалеке», «вверху», «внизу», «вон там» и т. п. можно сравнить с такими выражениями, как «в прошлом», «минуту назад» и т. д.). Наконец, теория растущего блока утверждает, что реально существуют только настоящее и прошлое, а будущее пока не существует и лишь постепенно реализуется в настоящем. То есть четырёхмерный пространственно-временной блок Вселенной растёт по мере превращения будущего в настоящее и прошлое.
Координаты
Реальные физические координаты – расстояния данной точки A до \(M\) точек отсчета в пространстве мерности \(N < M\). Этот метод позиционирования известен как трилатерация, применяемая в геодезии и радионавигации (GPS, ГЛОНАСС). Все другие координатные системы не абсолютны и производны. Точка A – пересечение \(M\) гиперсфер. Пример для 2D-пространства:
Реальные координаты пространства целой мерности зависимы друг от друга, то есть на данном примере две окружности имеют две точки пересечения, а третья должна пересечь одну из них, имея только два допустимых радиуса. Если мерность пространства \(2 < N < 3\), то пересечение двух окружностей содержит более двух точек, и третья окружность имеет больше допустимых радиусов, однозначно определяя координаты. Все координатно-векторные операции выполнимы с помощью решения систем треугольников. Линейная алгебра бесполезна в случае пространства дробной мерности.
Еще один пример для 1D-пространства:
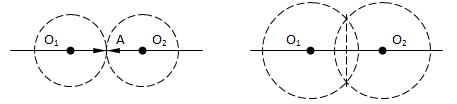
На данном рисунке справа показан известный метод построения перпендикуляра, существующего лишь в 2D-пространстве и более. При мерности \(1\leq N<2\), две гиперсферы могут иметь лишь одну точку пересечения A.
Физическое пространство имеет абсолютную систему отсчета, относительно которой определены абсолютные линейные скорости всех объектов.











