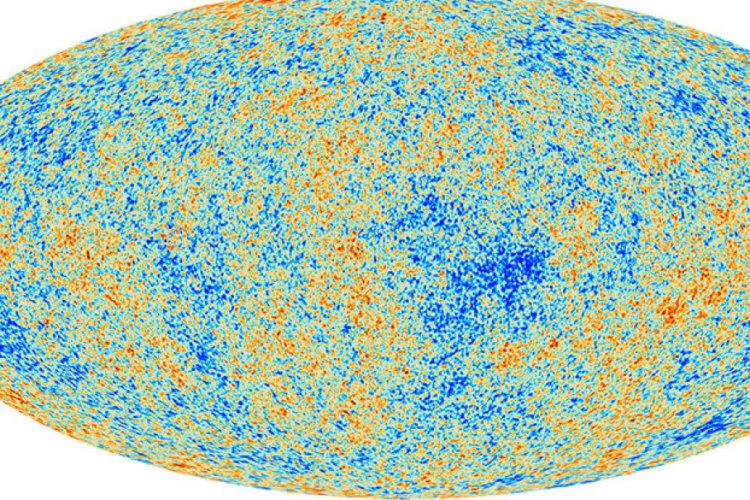
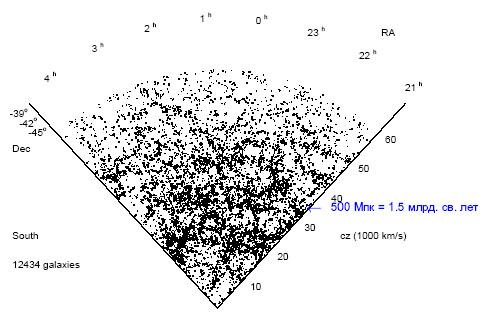
Изотропность пространства — это одно из фундаментальных свойств вселенной

Изотропное вещество

Вращение плоскости поляризации в изотропном веществе, находящемся в магнитном поле, было открыто Фарадеем в 1848 году.
 

Фарадей установил, что оптически изотропные вещества, помещенные в магнитном поле, делаются оптически анизотропными и приобретают способность вращать плоскость поляризации плоскополяризованного света, проходящего через вещество в направлении, параллельном линиям магнитных сил. Эллисон сконструировал установку ( см. фигуру), фиксирующую и регистрирующую эти весьма малые запаздывания.
 

Отметим, что в реакциях изотропных веществ с кубической симметрией поверхность раздела очень часто обладает идентичными свойствами во всех точках. Эти случаи представляют особый интерес и им необходимо отдавать предпочтение при тщательных кинетических исследованиях.
 

Расчеты показывают, что в однородном изотропном веществе в результате интерференции образуется проходящая полна, направление распространения которой совпадает с направлением первичной волны, а фазовая скорость зависит от частоты.
 

Расчеты показывают, что в однородном изотропном веществе в результате интерференции образуется проходящая волна, направление распространения которой совпадает с направлением первичной волны, а фазовая скорость зависит от частоты. В оптически неоднородной среде в результате наложения первичной и вторичных волн возникает рассеяние света. Наконец, при падении света на границу раздела двух различных сред в результате интерференции возникает не только проходящая, но и отраженная волна. Таким образом, отражение света происходит не от геометрвгаес-кой поверхности раздела сред, а от более или менее значительного слоя частиц среды, прилегающих к границе раздела.
 

Расчеты показывают, что в однородном изотропном веществе в результате интерференции образуется проходящая волна, фазовая скорость которой зависит от частоты, а направление распространения совпадает с направлением распространения первичной волны.
 

Ограничимся рассмотрением простейшего случая, когда однородное и изотропное вещество сплошь заполняет магнитное поле.
 

Ограничимся рассмотрением простейшего случая, когда однородное и изотропное вещество сплошь заполняет магнитное поле. Это можно реализовать, если на тороидальный сердечник из исследуемого вещества равномерно намотать обмотку, по которой течет ток. Вещество сердечника, естественно, намагнитится за счет действия магнитного поля тока.
 

Каким числом констант описываются упругие свойства изотропного вещества.
 

Зазор между двумя концентрическими сферами заполнен однородным изотропным веществом. Радиусы сфер равны: / 410 0 см и / — 212 0 см. Поверхность внутренней сферы поддерживается при температуре 7 320 К, поверхность внешней сферы — при температуре Г2300 К.
 

Зазор между двумя концентрическими сферами заполнен однородным изотропным веществом. Поверхность внутренней сферы поддерживается при температуре Т 320 К, поверхность внешней — при температуре Т 300 К.
 

Зазор между двумя концентрическими сферами заполнен однородным изотропным веществом. Поверхность внутренней сферы поддерживается при температуре 7 320 К, поверхность внешней — при температуре Г2 300 К.
 

Зазор между двумя концентрическими сферами заполнен однородным изотропным веществом.
 

Расчеты показывают, что в од неродном изотропном веществе в результате интерференции образуется проходящая волна, фазовая скорость которой зависит от частоты, а направление распространения совпадает с направлением распространения первичной волны.
 

Мышца состоит из двух различных элементов: изотропного вещества и анизотропного двоякопреломляющего вещества. Во время сокращения двоякопреломляющее вещество изменяет свою форму, а двойное лучепреломление уменьшается.
 

Изотропное твердое тело

Изотропные твердые тела обладают как объемной упругостью, так и упругостью формы. Поэтому в них возможны как продольные волны, так и поперечные.
 

Рассмотрим однородное изотропное твердое тело, нагретое каким-либо способом и затем охлаждающееся.
 

Для изотропных твердых тел тепловой поток в некоторой точке пропорционален градиенту температуры в этой точке, а вектор теплового потока направлен по нормали к изотермической поверхности, проходящей через эту точку. В случае же анизотропного твердого тела вектор теплового потока необязательно параллелен вектору градиента температуры, и поэтому направление вектора теплового потока может не совпадать с нормалью к изотермической поверхности. Поэтому, даже когда градиент температуры перпендикулярен данной поверхности, вектор теплового потока не перпендикулярен этой поверхности и не параллелен вектору градиента температуры.
 

Для изотропных твердых тел понятие давления применимо только в случае всестороннего растяжения и сжатия. В общем же — случае произвольной деформации напряженное состояние тела уже нельзя характеризовать одной скалярной величиной — давлением — и приходится пользоваться понятием тензора упругих напряжений ( см. Упругие волны.
 

Для изотропных твердых тел функция Рао отличается от найденной для тех же веществ, но находящихся в жидком состоянии.
 

Если внутри изотропного твердого тела имеется источник тепла, то уравнение ( 8 — 37) можно обобщить, прибавив член, учитывающий тепловыделение.
 

К относительно изотропным твердым телам относятся самые разнообразные вещества и материалы, например твердый криптой, хлорид натрия и алмаз, поэтому не удивительно, что при трении все они могут вести себя по-разному. Более мягкие твердые тела обычно подчиняются закону Амонтона и характеризуются нормальными значениями fi от 0 5 до 1 0, если только их температура не слишком близка к точке плавления. Ионные кристаллы, например хлорид натрия, также подчиняются закону Амонтона, хотя они обычно довольно хрупки, и вследствие этого их поверхности могут необратимо изменяться, в частности растрескиваться. Следовательно, площадь контакта таких кристаллов в основном определяется, по-видимому, пластичным течением, а не упругой деформацией.
 

В изотропном твердом теле имеются две скорости распространения, соответствующие чисто продольной и чисто поперечной волне.
 

В изотропных твердых телах могут распространяться как поперечные, так и продольные волны.
 

В изотропных твердых телах скорость распространения упругих волн зависит от вида волны, упругих постоянных и размеров тела, в котором волна распространяется.
 

В изотропном твердом теле одна ветвь акустического спектра отвечает продольным, а две другие-поперечным колебаниям; скорость продольных звуковых волн больше скорости поперечных волн. В анизотропном кристалле разделение волн на продольные и поперечные теряет, вообще говоря, смысл. Но в литературе часто называют условно продольной ветвь с наибольшей скоростью звука.
 

В изотропном твердом теле одна ветвь акустического спектра отвечает продольным, а две другие — поперечным колебаниям; скорость продольных звуковых волн больше скорости поперечных волн. В анизотропном кристалле разделение волн на продольные и поперечные теряет, вообще говоря, смысл. Но в литературе часто называют условно продольной ветвь с наибольшей скоростью звука.
 

Стекло представляет собой изотропное твердое тело, полученное переохлаждением расплава компонентов, среди которых хотя бы один является стеклообразующим. Критической температурой перехода от стеклообразного состояния к жидкостям является температура стеклования ст. Ей соответствует вязкость стекла 1012 Па-с. При нагреве стекло постепенно размягчается. Интервал температур 900 — 1300 С, в котором вязкость стекла уменьшается от 1012 до 108 Па-с, называется интервалом выработки.
 

Упругие деформации изотропного твердого тела можно рассматривать и с несколько иной точки зрения, чем это сделано выше. Заметим, что из рис. 7.3 следует неизменность объема каждого элемента тела при сдвиге. Поэтому сдвиг можно определить как такую деформацию, при которой меняется только форма тела, а объем его остается прежним.
 

О свойствах времени

Необходимо сказать еще несколько слов о времени. Поскольку время одномерно, оно может иметь два равноправных направления – это означало бы его полную обратимость, а значит, абсолютную изотропность и пространства, и времени. Однако за некоторыми особыми исключениями, относящимися к явлениям в мире элементарных частиц, мы не наблюдаем в природе обратимых процессов. Вселенная эволюционирует в одном направлении, заданном так называемой «стрелой времени». Это понятие связано с термодинамикой Вселенной как замкнутой системы, имевшей определенные начальные условия развития.

Время, таким образом, будучи однородным, поскольку в нем не имеется выделенных моментов (все точки на оси времени равноправны), не является изотропным.

Пространство и время в ньютоновской физике

Однородность и изотропность пространства – это ключевые понятия классической механики Галилея и Ньютона. Пространство в рамках этого учения мыслилось бесконечным, плоским, однородным, изотропным и абсолютным, то есть совершенно безразличным к распределению материи в нем. Пространство полагалось существующим только в качестве некоего места, где расположены физические тела, взаимодействующие между собой – но не со своим «вместилищем». Такое пространство могло служить идеальной, независимой ни от чего инерциальной системой отсчета.

Что касается времени, то его ньютоновская концепция определяет время также как некую самостоятельную, абсолютную категорию, относящуюся исключительно к длительности различных процессов. Время в ньютоновском понимании равномерно и синхронно для всей Вселенной, оно отделено от материи, от движущихся тел.

Анизотропность

Анизотропность ( в противоположность изотропности) — такое распределение всех или некоторых физических свойств в твердом теле, когда эти свойства различны по различным направлениям в теле.
 

Анизотропность — различие в свойствах материалов в направлении параллельно и перпендикулярно волокнам — обычно-исследуется на образцах, выпиленных из кускового материала.
 

Анизотропность этого материала обусловлена ориентацией в нем волокон в одном направлении. Поэтому СВАМ отличаются особенно высокой прочностью в продольном направлении и значительно меньшей — в поперечном.
 

Анизотропность может проявляться не только в кристаллах; так, например, дерево анизотропно, так как оно колется вдоль волокна легче, чем поперек, но дерево неоднородно. Кристаллы одновременно и однородны и анизотропны; свойства их по параллельным направлениям одинаковы, по непараллельным же могут быть различными.
 

Анизотропность — различие в свойствах материалов в направлении параллельно и перпендикулярно волокнам — обычно исследуется на образцах, выпиленных из кускового материала.
 

Анизотропность имеет большое практическое значение. Анизотропностью пользуются для изменения электрических свойств стали. Холодной прокаткой добиваются высоких магнитных и электрических свойств в определенном направлении, благодаря чему достигают значительного снижения потерь в трансформаторной стали.
 

Анизотропность имеет большое практическое значение. При глубокой штамповке изделий ( например, гильз, цилиндрических стаканов), если кристаллы в заготовке ориентированы неправильно, вытяжка во все стороны будет одинакова ( фиг. При штамповке из заготовки с правильной ориентировкой кристаллов вследствие неодинаковой вытяжки во все стороны по краям, стаканов ( патронов) получаются неровности ( уши), называемые фестонами ( фиг. Это приводит к массовому браку. Соответствующей термообработкой добиваются неправильной ориентировки кристаллов, предупреждая этим брак.
 

Анизотропность определяют иногда как отношение показателей буримости пород в двух взаимно перпендикулярных направлениях.
 

Анизотропность — различие в свойствах материалов в направлении параллельно и перпендикулярно волокнам — обычно исследуется на образцах, выпиленных из кускового материала.
 

Анизотропность свидетельствует об образовании мицелл, а изотропность о том, что вещества находятся в состоянии истинного раствора. Кроме того, первые два мыла поглощают воду, а последние два этой способностью не обладают.
 

Анизотропность — свойство, общее всем кристаллическим телам и являющееся их отличительной особенностью.
 

Анизотропность ( различие свойств вдоль и поперек волокон) у древесины проявляется больше, чем у других строительных материалов. Так, например, прочность при сжатии вдоль волокон в 2 — 4 раза больше, чем поперек волокон, а прочность при растяжении поперек волокон составляет примерно 1 / 20 — г / 4о от прочности при растяжении вдоль волокон.
 

Анизотропность этого материала обусловлена ориентацией в нем волокон в одном направлении. Поэтому СВАМ отличаются особенно высокой прочностью в продольном направлении и значительно меньшей — в поперечном.
 

Обращение времени в классической механике

Преобразование R{\displaystyle R} обращения времени в классической механике
задаётся правилами:

• xR=x{\displaystyle x^{R}=x}, pR=−p{\displaystyle p^{R}=-p}, где x{\displaystyle x} — координата, p{\displaystyle p} — импульс частицы.
• Физические величины, не являющиеся динамическими переменными (масса, заряд и т.д.), не изменяются при обращении времени.
• Для любой функции F{\displaystyle F} динамических переменных A,B,…{\displaystyle A,B,…} справедливо F(A,B,…)R=F(AR,BR,…){\displaystyle F(A,B,…)^{R}=F(A^{R},B^{R},…)}.
• Гамильтониан H{\displaystyle H} и пространственные координаты x{\displaystyle x} инвариантны относительно обращения времени

HR=H,xR=x{\displaystyle H^{R}=H,x^{R}=x}.

Свойства обращения времени в классической механике

• Пусть Q{\displaystyle Q} — произвольная динамическая переменная, H{\displaystyle H} — гамильтониан. Тогда справедливо равенство (Q,H)R+(QR,H)={\displaystyle (Q,H)^{R}+(Q^{R},H)=0}. Здесь (.){\displaystyle (.)} — скобки Пуассона.
• Пусть p{\displaystyle p} — импульс физической системы. Тогда pR=−p{\displaystyle p^{R}=-p}.
• Пусть F,G{\displaystyle F,G} — произвольные динамические переменные. Тогда справедливо равенство (F,G)R+(FR,GR)={\displaystyle (F,G)^{R}+(F^{R},G^{R})=0}. Здесь (.){\displaystyle (.)} — скобки Пуассона.
• Пусть Q{\displaystyle Q} — произвольная динамическая переменная. Тогда (dQdt)R=−dQRdt{\displaystyle ({\frac {dQ}{dt}})^{R}=-{\frac {dQ^{R}}{dt}}}.
• Пусть L{\displaystyle L} — лагранжиан физической системы. Тогда LR=L{\displaystyle L^{R}=L}.
• Изотропность времени. Изотропностью времени в классической механике называется одинаковость его свойств по обоим направлениям. Она следует из того, что замена переменной t{\displaystyle t} на −t{\displaystyle -t} в уравнениях Лагранжа оставляет их, и вытекающие из них уравнения движения, неизменными. Все движения по законам классической механики обратимы, то есть для всякого движения, описываемого уравнениями классической механики, всегда возможно обратное во времени движение, когда механическая система проходит те же состояния в обратном порядке..

Симметрия и законы сохранения

Все симметрии связаны с законами (иногда даже говорят о принципах – всеобщих закономерностях) сохранения. Например, однородность времени, то есть независимость от момента, в который существует физическая система, влечет за собой принцип сохранения энергии, однородность пространства – закон сохранения импульса (количества движения).

Следствием изотропности пространства является закон сохранения момента количества движения (углового, или кинетического момента). Это значит, что количество вращательного движения замкнутой системы безразлично к углу ее поворота относительно любой выбранной оси. Можно говорить также о прямолинейном движении системы мимо произвольной точки. Относительно нее наша система тоже обладает угловым моментом.

Часто возникающее недоумение по поводу изотропности (и однородности) вызвано обычно тем, что, наблюдая Вселенную на любом масштабе, мы видим, что вещество распределено и движется в ней крайне неоднородно и в различных точках, и в различных направлениях. Чтобы рассеять недоумение, достаточно представить себе, что далекая галактика переместилась или что мы убрали вазу со стола – ведь после этого в том направлении законы физики не перестали выполняться. Точно так же они будут работать независимо от того, проедет ли автомобиль мимо дома или на какой высоте и в какой плоскости расположена орбита спутника.

[править] Источники

1. С. Э. Шноль Парадоксы и проблемы интерпретации феномена макроскопических флуктуаций
2. С. Э. Шноль Макроскопические флуктуации — возможное следствие флуктуаций пространства-времени. Арифметические и космофизические аспекты
3. Jere H. Jenkins, Ephraim Fischbach, John B. Buncher, John T. Gruenwald, Dennis E. Krause, Joshua J. Mattes [http://arxiv.org/PS_cache/arxiv/pdf/0808/0808.3283v1.pdf Evidence for Correlations Between Nuclear Decay Rates and Earth-Sun Distanc]
4. Eric B. Norman, Edgardo Browne, Howard A. Shugart, Tenzing H. Joshi, Richard B. Firestone Evidence against correlations between nuclear decay rates and Earth-Sun distance
5. Китайские ученые подтвердили анизотропность Вселенной
6. Понятие темной энергии происходит из попытки объяснить то, что Постоянная Хаббла не постоянная, и наша вселенная расширяется с ускорением, и необходима энергия для ускоренного «расталкивания» масс
7. 30-ая минута фильма Анизотропный мир
8. G.Cocconi and E.Salpeter, Nuovo Cimento, 10, 646, 1958
9. V.Beltran-Lopez, H.G.Robinson and V.W.Hughes, Bull. Am. Phys. Soc., 6, 424, 1961; R.W.P.Drever, Phil. Mag., 6, 683, 1961

Как вычислить анизотропию?

Все написанное выше, мы надеемся, достаточно ясно рассказало читателю, что такое анизотропия. Однако возникает и другой вопрос: как посчитать, насколько различаются свойства вдоль несовпадающих направлений в твердых телах? Для этого есть коэффициент анизотропии. Сразу оговоримся, для каждой величины он вычисляется по-своему. Показатели, испытывающие анизотропию, могут быть непохожи друг на друга. Свойства механической или квантовой системы различаются кардинально, что приемлемо для одной, для другой будет невыполнимо или вовсе невозможно. Поэтому говорить о некоем общем для любой величины коэффициенте не стоит. К тому же чаще всего вычислить его чисто теоретически не представляется возможным, эту величину получают только опытным путем. Коэффициент анизотропии включает соотношение значений исследуемой величины в разных направлениях. Иногда этот показатель включает угол между выбранными направлениями. Правда, чаще всего лишь как показатель у основания значения величины. Например, К_ху показывает, что данный коэффициент относится к разнице значений физической величины вдоль осей икс и игрек.

Какой угол нужен для анизотропии?

Выше мы привели пример, когда распространение звука неодинаково во взаимно поперечных направлениях. Это частный случай того, как проявляется анизотропия свойств, который называется термином «оротропия». Однако симметрия кристаллов бывает не только кубической или ромбической. Она бывает тригональной, когда повтор элементов структуры происходит при повороте на треть круга, или даже гексагональной, тогда угол поворота равняется одной шестой круга. Симметрия низшей категории, моноклинная, дает возможность свойствам быть неодинаковыми в кристалле в трех взаимно не перпендикулярных направлениях. Таким образом, анизотропия – это качество кристаллических тел, которое может проявляться под любыми углами как в одной плоскости, так и в объеме.

Понятие об однородности и изотропности

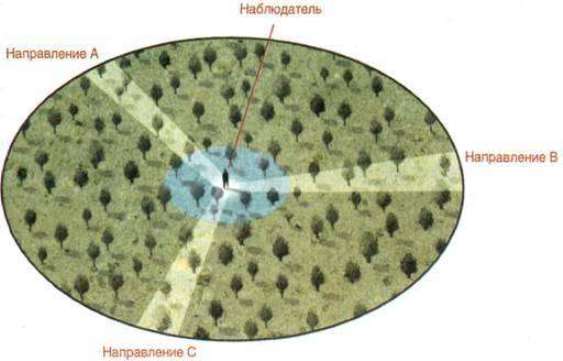
Однородность означает отсутствие в пространстве выделенных точек. Все местоположения одинаковы и равноправны по отношению к действию законов природы, и последние не изменяются при переходе (трансляции) из одной точки в другую. То есть, в пространстве Вселенной на всем его протяжении действуют одни и те же законы, и параллельный перенос любой замкнутой физической системы никак не отразится на ее функционировании.

Изотропностью пространства называют отсутствие в нем выделенных, особых направлений. Какую бы ориентацию в пространстве мы ни избрали, на какой бы угол ни поворачивали систему отсчета, законы природы не изменят своего действия – все направления равноправны. Никакое изменение ориентации замкнутой системы не может повлиять на ее свойства.

Определение ортотропных свойств оболочек

Для плоской оболочки, выберите плоскость, параллельную оболочке в качестве справочной геометрии. Оси X и Y лежат на плоскости, и ось Z перпендикулярна плоскости. Для цилиндрической оболочки, выберите ось цилиндра в качестве справочной геометрии. Ось Y является параллельной оси цилиндра, ось X является тангенциальной.

В композитных оболочках из ортотропного материала, определение направлений X, Y и Z различно для каждого слоя, в зависимости от угла ориентации волокон слоя композита. Справочная геометрия не учитывается при определении ортотропных материалов.

В основном, программа изменяет справочную геометрию следующим образом:

• Программа преобразует определенную справочной геометрией систему координат, устанавливая ось Z перпендикулярно плоскости оболочки. Плоскость оболочки определяется 3 угловыми узлами.

• При значении угла между осью X выбранной справочной геометрии и перпендикуляром к плоскости оболочки более 45o, ось X справочной геометрии отображается программой на плоскость оболочки, для определения измененной оси X.

• При значении угла между осью X выбранной справочной геометрии и перпендикуляром к плоскости оболочки менее 45o, ось Y справочной геометрии отображается программой на плоскость оболочки, для определения измененной оси X.

• Затем, определяется ось Y измененной справочной геометрии, для завершения правосторонней Декартовой системы координат.

Где еще бывает анизотропия?

Когда человек слышит «кристаллы», обычно представляет себе полупрозрачные столбики кварца или аметиста. Некоторые девушки наверняка думают об украшениях. Однако кристаллическим может быть любое твердое тело. Изделия из железа, алюминия, меди, олова тоже состоят из кристаллов, только очень маленьких. И в каждой такой вещи на микроуровне также наблюдается анизотропия металлов. Однако свойства, которые распространяются в перпендикулярных направлениях по-разному, весьма специфические и в повседневной жизни незаметны. Например, в кубических кристаллах железа и алюминия модули упругости Юнга меняются в зависимости от выбранной оси. А линейное расширение олова в разных направлениях различается почти в два раза. Однако такие подробности, как правило, не требуется учитывать каждый день. Ведь анизотропия металлов и её последствия, как правило, закладываются во все возможные их применения на стадии проектирования вещей, зданий, самолетов, машин.

Анизотропное тело

Анизотропные тела как объекты, свойства которых зависят от ориентации системы координат, имеют более сложную систему параметров, характеризующих диссипацию энергии.
 

Нейтрально устойчивые анизотропные тела, такие, как эллипсоиды, ведут себя более интересно, чем изотропные. Хотя первые падают устойчиво при любой ориентации, они, вообще говоря, не падают вертикально вниз, если только они случайно не были опущены в жидкость так, — то одна из главных осей поступательного движения оказалась параллельной направлению поля тяжести. Во всех других случаях такие тела в процессе оседания дрейфуют также и в боковом направлении. Количественным примером поведения такого типа является движение круглого диска, рассматриваемое далее в этом разделе.
 

Когда анизотропное тело обладает упругими свойствами, симметричными относительно трех взаимно перпендикулярных плоскостей, оно называется ортогонально-анизотропным или ортотропным. Пусть координатные оси х, у, z направлены по линиям пересечения плоскостей симметрии упругих свойств. Тогда симметричными относительно координатных плоскостей будут компоненты тензоров напряжений и деформаций cfx, ау, az, ех, еу, е, кососиммет-ричными — касательные напряжения txy, — сух, zx и соответствующие им деформации сдвига у-ху, чу угх. Следовательно, для ортотропного тела при принятой системе координат в формулах (1.37), ( 1 39) коэффициенты, связывающие нормальные напряжения с деформациями сдвига и касательные напряжения с деформациями удлинения, обращаются в нуль. В силу симметрии упругих свойств тела относительно координатных плоскостей должны также отсутствовать коэффициенты, связывающие деформации сдвига в одной координатной плоскости с касательными напряжениями, действующими в других координатных плоскостях.
 

Однако анизотропные тела проявляют особенности в процессе линейного теплового расширения: многие высокоориентированные полимеры при нагревании в определенных температурных интервалах показывают в направлении ориентации обратимые сокращения. В последнее время указанное поведение ориентированных полимеров было отмечено и на ряде других полимеров: полиэтилене, полипропилене, поливиниловом спирте, политрифторэтилене и поликапроамиде.
 

Если анизотропное тело обладает какой-либо присущей ему симметрией, то появляются дополнительные соотношения между модулями упругости и тем самым уменьшается число независимых модулей.
 

Рассмотрим теперь анизотропное тело с трещинами.
 

Пусть однородное анизотропное тело имеет в каждой точке плоскость упругой симметрии, параллельную данной плоскости, которую мы примем за плоскость Оху.
 

Для анизотропных тел, обладающих дополнительными условиями симметрии, число независимых упругих характеристик снижается в соответствии с этими условиями, и для случая изотропного тела оно доходит до двух пар. Если, кроме того, тело несжимаемо, то остается только одна пара упругих характеристик, напр. Юнга ( или модуль сдвига) и соответствующая ему функция памяти.
 

Для анизотропных тел в формулу работы входит члены, содержащие работу формы и объема, и разделение затрудняется ( см. гл.
 

Для анизотропного тела обобщенный закон Гука существенно усложняется: он отражает прямую пропарщи-нальность между каждым компонентом тензора деформаций и всеми шестью независимыми компонентами тензора напряжений.
 

Теплопроводность анизотропных тел, как и линейное расширение, вообще говоря, различна в разных направлениях.
 

У анизотропных тел коэффициент линейного расширения зависит от направления. Это означает, что происходит неодинаковое расширение по различным направлениям, которое приводит к изменению формы тела при нагревании.
 

Структура анизотропного тела может обладать некоторой упругой симметрией, в каждой точке тела обнаруживаются симметричные в отношении упругих свойств направления. В этих случаях оказывается возможным выбрать такую ориентацию осей координат, при которой некоторые упругие постоянные оказываются равными нулю или линейно зависящими от других упругих постоянных.
 

Для анизотропного тела вводятся тензор-операторы четвертого ранга, заменяющие упругие константы в законе Гука.
 

Для анизотропного тела Q — зависит также от выбранных направлений в начальном состоянии.
 

Однородность и изотропность пространства-времени

Специальная теория относительности показала, что пространство и время не абсолютны и не отделены друг от друга, а представляют собой тесно взаимосвязанные категории, участвующие в движении материи. Пространство-время представляет собой четырехмерный континуум – топологическое многообразие, точками которого являются не местоположения и моменты отдельно и независимо друг от друга, а события, определяемые четырьмя координатами в конкретной системе отсчета.

Общая теория относительности дополнила представления о пространстве-времени, рассматривая его как объект, тесно связанный с распределением и поведением движущихся масс материи – вещества и полей. Может показаться, что такое понимание противоречит тезису об изотропности пространства. Это, однако, не так. В четырехмерном континууме нет выделенных событий, все они равноправны по отношению к законам природы, поэтому пространство-время однородно. В некотором смысле можно говорить и о своеобразной изотропии континуума, так как время в нем тесно увязано с пространством. Но термодинамическая «стрела времени» накладывает весьма жесткое (хотя и вероятностное по характеру) ограничение на изотропность времени.

Определение анизотропии

Для начала дадим определение этого понятия. Анизотропия – это различие свойств и параметров объекта в разных направлениях. Получается слегка непонятно и явно требует пояснения. Под свойствами понимаются любые характеристики веществ – упругость, скорость звука, показатель преломления, теплопроводность, электропроводность. Таким образом, например, для скорости звука анизотропия – это такое явление, когда поперек каменной глыбы звуковые волны распространяются с другой скоростью, чем вдоль. В данном случае это свойство помогает определить породы, залегающие в глубине земной коры. Естественное распространение при землетрясении, например, или при специально созданном сильном ударе даст представление о плотности и угле залегания разных полезных ископаемых.