Что такое фрактал? фракталы в природе

История появления.

Первые идеи фрактальной геометрии
возникли в 19 веке. Кантор с помощью простой
рекурсивной (повторяющейся) процедуры
превратил линию в набор несвязанных точек (так
называемая Пыль Кантора). Он брал линию и
удалял центральную треть и после этого
повторял то же самое с оставшимися
отрезками. Пеано нарисовал особый вид линии
(рисунок №1). Для ее рисования Пеано
использовал следующий алгоритм.

На первом шаге он брал прямую линию и заменял ее на 9 отрезков длинной в 3 раза меньшей, чем длинна исходной линии (Часть 1 и 2 рисунка 1). Далее он делал то же самое с каждым отрезком получившейся линии. И так до бесконечности. Ее уникальность в том, что она заполняет всю плоскость. Доказано, что для каждой
точки на плоскости можно найти точку, принадлежащую линии Пеано.
Кривая Пеано и пыль Кантора выходили за рамки обычных геометрических объектов. Они не имели четкой размерности. Пыль Кантора строилась вроде бы на основании одномерной прямой, но состояла из точек (размерность 0). А кривая Пеано строилась на основании одномерной линии, а в результате получалась плоскость.
Во многих других областях науки появлялись задачи, решение которых приводило к странным результатам, на подобие описанных выше (Броуновское движение, цены на акции).

СМИ ПОН

Что такое фракталы: бесконечность и красота математики

Подлинная история советского «ограбления века». Дело братьев Калачян

В 1977 году в Армении произошло крупнейшее в истории СССР ограбление Госбанка.

Об ограблении денежных хранилищ Госбанка не думали даже матёрые уголовники. И тем не менее в 1977 году случилось немыслимое — злоумышленники покусились на святая святых советской финансовой системы.

Операция «Архив». Как Советский Союз окончательно избавился от Гитлера

На рубеже 1980–1990-х годов, когда в Восточной Европе произошло обрушение просоветских режимов, а Западная Германия поглотила Восточную, произошло резкое усиление позиций неонацистов.

На фоне ниспровержения социализма крайне правые силы пытались добиться хотя бы частичной реабилитации нацизма.

Непобедимая страна. 15 интересных фактов о Советском Союзе

30 декабря 1922 года на Первом Всесоюзном съезде Советов было утверждено образование Союза Советских Социалистических республик. Советский Союз занимал территорию площадью 22 400 000 квадратных километров, являясь самой большой страной на планете, имел самую протяжённую границу в мире (свыше 60 000 километров) и граничил с 14 государствами.

Великая душа. Жизнь и принципы Махатмы Ганди

Мохандас Карамчанд Ганди родился 2 октября 1869 года в индийском городе Порбандар в состоятельной семье из варны вайшьев. Маленький Мохандас, или Мохан, меньше всего напоминал философа, мыслителя и политика, идеи которого перевернут мир.

Продукт гуманизма. Как сердобольный дантист придумал «электрический стул»

6 августа 1890 года человечество вписало новую страницу в свою историю. Научно-технический прогресс добрался и до такого специфического рода деятельности, как исполнение смертных приговоров. В Соединённых Штатах Америки была проведена первая смертная казнь на «электрическом стуле».

Придуманный из гуманных соображений «электрический стул» оказался одним из самых жестоких способов смертной казни.

Индикатор fractals в торговом терминале Meta Trader 4

Индикаторы Билла Вильямса не требуют установки и входят в стандартный набор индикаторов, доступных трейдеру «из коробки». Для того, чтобы прикрепить индикатор фрактал в терминале Мета Трейдер 4 к графику необходимо: в главном меню (или в окне «Навигатор») выбрать пункт меню «Вставка» — «Индикаторы» — «Билла Вильямса» — «Fractals»:

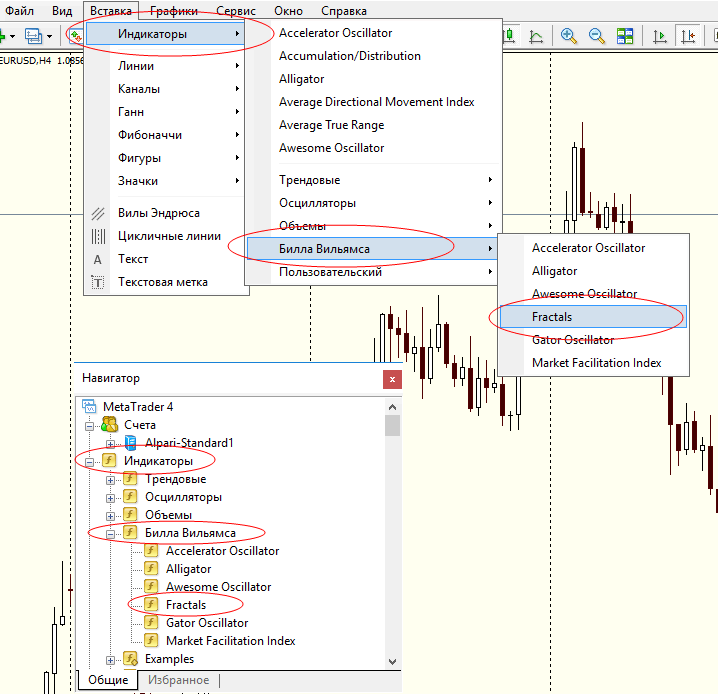
Индикатор фрактал с настройками периода

Стандартный индикатор для МТ4 не имеет никаких настроек, кроме цветовых. Его использование с периодом «5» сводит на нет все возможности и преимущества данного инструмента. Но для Мета Трейдера существует множество кастомных (пользовательских) индикаторов, которые помогут решить нашу проблему.

Например, такие:

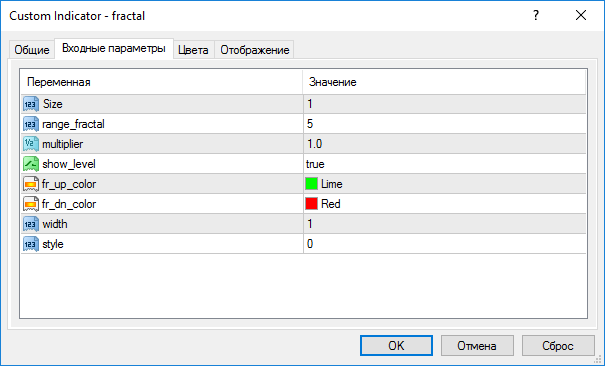
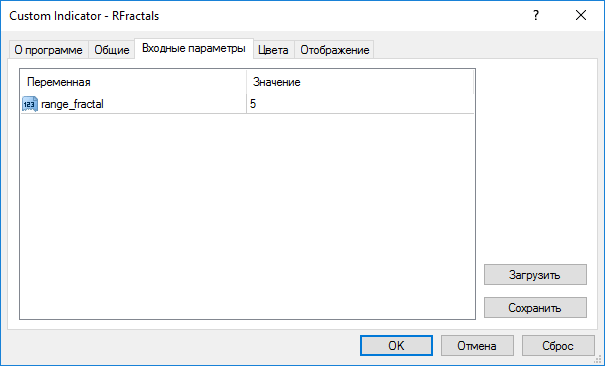
Вот ссылка:

Контент только для зарегистрированных пользователей! , чтобы получить доступ к контенту.

Заключение

Вот, друзья, мы и добрались до завершающей части статьи. Пришло время резюмировать пройденный материал подвести итоги.

Я постарался максимально подробно рассказать Вам об индикаторе фракталов. Вы узнали о том, что это такое такое, историю о том, как они пришли в трейдинг, а также как использовать их на практике. На мой взгляд, это очень интересный инструмент, который однозначно стоит Вашего внимания! Однако, я бы не стал рекомендовать использовать этот индикатор в его классической интерпретации. В ней он представлен как классический трендовый индикатор пробойного типа, рассчитанный на «ловлю» крупных трендовых движений. Возможно, он будет работать на старших временных интервалах рынка акций, но вряд ли сможет показать хорошие результаты на краткосрочных фьючерсных и валютных рынках.

Тем не менее, не стоит сбрасывать его со счетов. Я показал Вам несколько интересных способов использования, как бы это парадоксально не звучало, технического индикатора в безиндикаторной торговле price action, среди которых и определение тренда с помощью индикатора fractals, построение областей поддержки-сопротивления и линий тренда.

Если у Вас остались вопросы после прочтения статьи, а может есть практический опыт использования инструментов Билла Вильямса, то обязательно напишите в комментариях. На этом все

Спасибо за внимание и успехов в торговле!

С уважением, Вадим Атрощенко

Ссылки[править]

Программы для генерации фрактальных изображенийправить

• Ultra Fractal — пожалуй, самая мощная программа, предназначенная для создания и анимации изображений по фрактальному алгоритму;
• Fractal Explorer — одна из лучших на сегодняшний день программ для создания изображений фракталов;
• XaoS — многоплатформенный генератор фракталов, позволяет приближать и удалять картинку в реальном времени;
• Fractint — очень мощная многоплатформенная программа, развитие которой, к сожалению, давно остановилось;
• Chaoscope — программа трёхмерной визуализации странных аттракторов;
• Apophysis — программа для создания fractal flames. Fractal flames является расширением IFS фракталов;
• RPS/Fract — несложный бесплатный генератор фракталов для платформы Pocket PC (PDA);
• P.Fract — несложный бесплатный генератор фракталов для платформы Palm (PDA);
• EyeFract
• Mfract
• Gnofract 4D
• IFS Illusions — Искусственное искусство программа и галереи

Сайты о фракталахправить

• Геометрические фракталы
• Фрактальные множества Очень подробная и качественная статья, начиная с комплексных чисел (Санкт-Петербургский государственный университет: ПМ-ПУ)
• Fractal World — сайт, на котором представлена широкая подборка видов фракталов с текстами программ для их построения;
• Архивохранилище Фрактал опубликовало на USENET
• Фракталы и теория хаоса
• Поверь алгебру гармонией Руководство к программе FractalExplorer на русском
• Введение во фракталы
• Доступно о фракталах
• Фракталы в НГУ: описания, форум, программа IFS Builder 3d
• Фракталы от OCo
• Фракталы и знание
• Всё о фракталах
• Красивая жизнь комплексных чисел
• Fractals of aramin (eng)
• Электронная библиотека по нелинейной динамике — книги о фракталах
• Программка, чтобы попробовать фракталы руками
• Фракталы, мультифракталы и не только
• Каталог сайтов о фракталах
• Фракталы в литературе: в поисках утраченного оригинала

Первоисточник этой статьи был признан «избранной статьёй» в русском разделе Википедии

Алгебраические фракталы

Эта группа фракталов строится на основе алгебраических формул, зачастую очень простых . Различают линейные и нелинейные алгебраические фракталы. Первые определяются линейными функциями (уравнениями первого порядка), а вторые – нелинейными (их природа значительно ярче, богаче и разнообразнее).

В общем виде фракталы данного класса могут быть получены на основе рассмотрения некоторых нелинейных процессов в n-мерных пространствах (в настоящее время наиболее изучены лишь двухмерные процессы). В связи с этим любой рассматриваемый нелинейный итерационный процесс может интерпретироваться как дискретная динамическая система.

Как известно (из синергетических представлений), нелинейные динамические системы могут иметь несколько устойчивых состояний. При этом состояние, в котором оказалась динамическая система после определенного конечного числа итераций, напрямую зависит от ее начального состояния. А это значит, что изучаемая система может рассматриваться в некотором фазовом пространстве, в котором будут присутствовать области притяжения (аттракторы). Рассматривая двумерное фазовое пространство и окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет любой системы. Применение различных алгоритмов выбора цвета позволяет получить достаточно сложные фрактальные картины с удивительными многоцветными узорами.

Классическим примером алгебраических фракталов является множество Мандельброта, описанное еще в 1905 г. французским математиком Пьером Фату и впервые построенное Мандельбротом в 1980 г. Алгоритм построения множества Мандельброта использует единственную простую итерационную формулу:

,

где z и c – комплексные величины, i – номер итерации.

В результате многократных итераций на плоскости образуется множество точек, выстраивающихся в сложной закономерности (рис. 10).

Доказано, что все точки, составляющие множество Мандельброта, целиком расположены внутри круга радиуса 2 на плоскости с центром в точке (0, 0). На практике при построении множества Мандельброта принято считать, что если для некоторой точки А последовательность итераций функции после некоторого их числа N (например, превышающих 100) не вышла за пределы этого круга, то точка принадлежит множеству и красится в черный цвет. Если же на какой-то итерации, меньшей N, элемент последовательности, определяемый на основе (1) по модулю стал больше 2, то он считается не относящимся к множеству. Основываясь на таком правиле, можно получить черно-белое изображение множества Мандельброта.

Рис. 10. Множество Мандельброта

Однако черно-белое множество не так привлекательно, поэтому в настоящее время принято отображать множества в цвете. Для этого можно, например, каждую точку не из множества красить в цвет, соответствующий номеру итерации, на котором ее последовательность выходит за пределы круга. Так, на рис. 10 при отображении множества Мандельброта применен наиболее распространенный способ построения цветного изображения множества, при котором точки, принадлежащие множеству, окрашиваются в черный цвет, а не принадлежащие множеству окрашиваются в цвет, соответствующий количеству итераций, за которое точка покидает окружность (построение выполнено в программе Fractal Explorer 2.02). Точки на границе множества, где возникают сложные структуры, уходят в бесконечность за конечное число итераций (аттрактор такой динамической системы находится в бесконечности).

К наиболее известным алгебраическим фракталам также относятся множества Жюлиа (рис. 11 – построение выполнено в программе Graphic v4.2007, рис. 12 – построение выполнено в программе Фракталы) и Бассейны Ньютона (рис. 13, построение выполнено в программе Fractal Explorer 2.02, рис. 14 – построение выполнено в программе Ultra Fractal 5).

Семейство множеств Жюлиа строится по той же итерационной формуле, что и множество Мандельброта, однако в качестве комплексной переменной используется лишь параметр c. Если в качестве значений комплексной переменной c использовать координаты точек, принадлежащих множеству Мандельброта, то множество Жюлиа при построении будет замкнутым.

Рис. 11. Множество Жюлиа (1)

Рис. 12. Множество Жюлиа (2)

Рис. 13. Бассейны Ньютона (1)

Рис. 14. Бассейны Ньютона (2)

Фракталы и хаос.

Понятие фрактал неразрывно связано с понятием хаос. Хаос — это отсутствие предсказуемости. Хаос возникает в динамических системах, когда для двух очень близких начальных значений система ведет себя совершенно по-разному. Пример хаотичной динамической системы — погода. Метеорологи шутят: «Взмах крыла бабочки в Техасе приводит к урагану во Флориде». Поэтому, когда будете слушать следующий прогноз погоды перед полетом на самолете вспомните эту статью 🙂

Хорошо проиллюстрировать хаотичное поведение можно с помощью так называемого logistic equation x=c*x(1-x). Пришло это выражение из биологии, т.к. это грубая модель популяции животных. Так вот при исследовании поведения этой функции выяснилась интересная ее особенность. Если с — фактор роста популяции находится в пределах от 1 до 3, то через некоторое количество итераций популяция стабилизируется.

При с=3 наша функция раздваивается — через определенное число итераций приходим к ситуации, когда высокая популяция в один год сменяется низкой в следующий и значение выражения как бы скачет между двумя значениями.

При с=3.45 она раздваивается снова и у нас уже имеется четырехлетний цикл.

Далее при росте с функция раздваивается все быстрее и быстрее: при с=3.54, с=3.564, с=3.569 …

И в точке 3.57 начинается хаос. Значения выражения не имеют какой либо периодичности или структуры. На рисунке изображена зависимость поведения функции от величины с.

Ну и на закуску интересный пример. Вы ведь доверяете своему компьютеру? Я имею в виду
вы считаете, что он очень точная и быстрая машина. Тогда запустите Microsoft Excel. Введите в ячейки А1 и B1 значение 4. В ячейки A2
и B2 одинаковые значения между 0 и 1. В ячейку A3 введите формулу «=$A$1*A2*(1-A2)», а в ячейку B3 введем ту же формулу, только раскроем скобки «=$B$1*(B2-B2*B2)», а в ячейку С3 поместим формулу разности «=A3-B3». Как и следовало ожидать результаты в ячейках A3 и B3, а разница равна 0. Теперь выделяем диапазон A3:C3 и копируем его в нижние 100 строк и смотрим что у нас происходит. Начиная с 5-7 строки мы видим, что появилась небольшая разница в результате 2 формул. Эта разница довольно быстро возрастает и на 50 шагу эта разница уже по величине равна нашим числам. Более того разные процессоры будут давать разные результаты. Возникает закономерный вопрос: какое же значение верно? Правильный ответ: «Никакое!». Начиная с определенного места ВСЕ современные компьютеры дают неверный результат. Вот такой простой задачкой мы поставили нашего «мистера-точность» в тупик :(.

Еще раз вспомните про прогноз погоды и самолеты. А ведь это только цветочки…

Вот и подошла к концу наша экскурсия в мир фракталов. Надеюсь она Вам понравилась. Я только немного приоткрыл Вам завесу в мир фракталов.

Если хотите изучить фракталы поподробнее зайдите на страничку http://www.eclectasy.com/fractovia/. Вы найдете там десятки программ рисования фракталов, некоторые с хорошими объяснениями.

Если Вы неплохо знаете английский, то лучше документации, чем та которая распространяется с программой Fractint не найти.

Вопросы можете задавать лично по адресу mailto:sakva@narod.ru

Описание индикатора фрактал (fractals)

Только лишь к 11 главе книги Билл Вильямс начинает знакомить нас с фракталами. Он говорит о том, что существует два вида фракталов: на покупку (фрактал вверх) и на продажу (фрактал вниз), а также дает их определение:

1. Фрактал на покупку — это последовательность из пяти баров (свечей), в которой максимум центрального (третьего) бара выше двух предыдущих и двух последующих баров.
2. Фрактал на продажу — это последовательность из пяти баров (свечей), в которой минимум центрального бара ниже выше двух предыдущих и двух последующих баров.

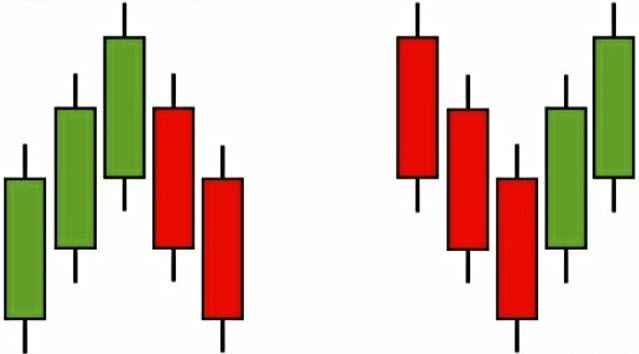
На этом рисунке изображен так называемый «классический» или «чистый фрактал». Его особенность состоит в том, что максимумы (минимумы) первых двух баров последовательно растут, третий бар формирует самый высокий экстремум, а максимумы (минимумы) четвертого и пятого баров последовательно снижаются. Такую разновидность фракталов весьма просто визуализировать. Для этого надо всего лишь взглянув на ладонь своей руки.

Так как максимумы (минимумы) последующих и предыдущих баров могут принимать любые значения, при условии, что они не будут выше (ниже) экстремума центрального бара, то можно выделить еще несколько разновидностей фракталов:

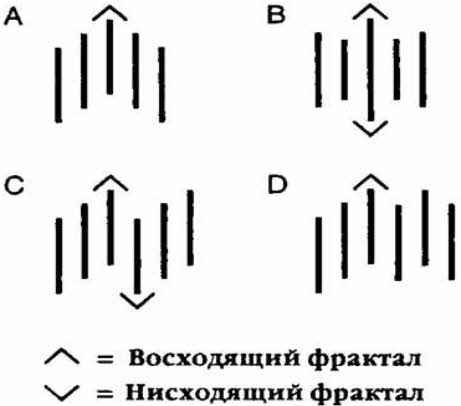
• На примере «В» продемонстрирован бар, который одновременно является как фракталом на покупку, так и на продажу.
• Пример «С» показывает, что разнонаправленные фракталы могут иметь общие бары.
• В примере «D» мы видим, что иногда для формирования фрактала необходимо более, чем 5 баров, при условии, что экстремум одного из последующих баров равен центральному.

Геометрические фракталы[править]

Кривая Коха

История фракталов началась с геометрических фракталов, которые исследовались математиками в XIX веке. Фракталы этого класса — самые наглядные, потому что в них сразу видна самоподобность.

В двухмерном случае такие фракталы можно получить, задав некоторую ломаную, называемую генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры (а точнее, при переходе к пределу) получается фрактальная кривая.
При видимой сложности полученной кривой, её общий вид задается только формой генератора.

Примерами таких кривых служат:

• кривая дракона;
• кривая Коха;
• кривая Леви;
• кривая Минковского;
• кривая Пеано.

К геометрическим фракталам также относят фракталы, получаемые похожими процедурами, например:

• множество Кантора;
• треугольник Серпиньского;
• коврик Серпиньского;
• кладбище Серпиньского;
• губка Менгера;
• дерево Пифагора.

Л. Карпентер: искусство, созданное природой

Теория фракталов довольно быстро нашла практическое применение. Так как она весьма тесно связана с визуализацией самоподобных образов, то первыми, кто взял на вооружение принципы и алгоритмы построения этих необычных форм, стали художники. Первым из них стал будущий основатель студии Pixar Лорен Карпентер. Работая над презентацией прототипов самолетов, ему в голову пришла идея в качестве фона использовать изображение гор. Сегодня с такой задачей сможет справиться практически каждый пользователь компьютера, а в семидесятых годах прошлого века ЭВМ были не в состоянии выполнять такие процессы, ведь графических редакторов и приложений для трехмерной графики на тот момент еще не было. И вот Лорену попалась книга Мандельброта «Фракталы: форма, случайность и размерность». В ней Бенуа приводил множество примеров, показывая, что существуют фракталы в природе (фыва), он описывал их разнообразную форму и доказывал, что они легко описываются математическими выражениями. Данную аналогию математик приводил в качестве аргумента полезности разрабатываемой им теории в ответ на шквал критики от своих коллег. Они утверждали, что фрактал — это всего лишь красивая картинка, не имеющая никакой ценности, являющаяся побочным результатом работы электронных машин. Карпентер решил опробовать этот метод на практике. Внимательно изучив книгу, будущий аниматор стал искать способ реализации фрактальной геометрии в компьютерной графике. Ему понадобилось всего три дня, чтобы визуализировать вполне реалистичное изображение горного ландшафта на своем компьютере. И сегодня этот принцип широко используется. Как оказалось, создание фракталов не занимает много времени и сил.

Немного сухих фактов

Само слово «фрактал» с латыни переводится как «частичный», «разделенный», «раздробленный», а что касается содержания этого термина, то формулировки как таковой не существует. Обычно его трактуют как самоподобное множество, часть целого, которая повторяется своей структурой на микроуровне. Этот термин придумал в семидесятых годах ХХ века Бенуа Мандельброт, который признан отцом фрактальной геометрии. Сегодня под понятием фрактала подразумевают графическое изображение некой структуры, которая при увеличенном масштабе будет подобна сама себе. Однако математическая база для создания этой теории была заложена еще до рождения самого Мандельброта, а вот развиваться она не могла, пока не появились электронные вычислительные машины.