Божественная гармония: что такое золотое сечение простыми словами. тайны мироздания в числах

Практика применения Фибо

Так зачем же она нам нужна? Мы наблюдаем, что уровни на линии Фибоначчи – это уровни потенциальной коррекции и возвращения к тренду.

У нас произошло окончание коррекции на уровне 50%:

Я думаю, все понимают, что вот эта свеча с очень большим хвостом была всего лишь обманным движением и выступила в качестве «пружины»:

Но даже если рассматривать ее хвост, то он приходится на уровень 61.8% от нашего существующего отрезка. Мы можем рассматривать для потенциального входа на рынок уровни 38.2, 50, 61.8 и 78.6. Сами по себе они не несут какой-то сверхсильной мощности, и просто открывая ордера на покупку, когда цена дошла до 38.2% или до 50%, вы не добьетесь прибыльности в трейдинге.

Эти уровни нужно использовать только в сочетании с другими элементами технического анализа. Допустим, если вы торгуете по графическим паттернам, то образовавшийся паттерн пин-бар может рассматриваться как точка для входа, так как он опирается на уровень 61.8. Таким образом графическая фигура получает точку опоры, и мы можем открыть сделку на покупку, имея основание в виде графического паттерна и уровня Фибоначчи.

А просто потому, что цена достигла уровня Фибо, открывать сделку не стоит.

Представим, что мы вошли в сделку, что-то заработали и цена двинулась выше, достигнув нового максимума. Что мы делаем далее?

Просто перетягиваем сетку выше на новый максимум:

Минимум тренда остаётся тем же.

И опять получаем уровни для потенциального окончания коррекции. Как мы видим у нас цена вначале застопорилась на 38.2%:

А потом достигла уровня 50%, и тренд вверх продолжился. Как только цена достигает отметки 38.2%, это не значит, что нужно сразу же срочно покупать:

Вы должны использовать уровни Фибо только в сочетании с какими-то другими торговыми индикаторами или стратегиями.

Если вы видите, что цена достигает уровня Фибо и возможен отскок, тогда можно закупиться. А если нет никаких сигналов на то, что сейчас произойдёт, кроме того, что цена достигла уровня коррекции, то тогда ничего не делаем. Уровни Фибо являются вспомогательным инструментом, но ни в коем случае не основным.

Разберём ещё один пример, но только с нисходящим трендом.

В самом его начале цена шла вниз, потом замедлилась и началась коррекция. Нам нужно определить, где она может потенциально закончиться, и на каких уровнях нам следует искать точки входа в рынок.

Выбираем инструмент Линии Фибоначчи. Для нисходящего тренда нам нужно отметить мышкой самую верхнюю точку, там, где тренд начался и, не отпуская левой кнопки, довести нашу сетку до уровня, где, по нашему мнению, началась коррекция:

В первый раз цена отбилась от уровня 38.2, нового минимума не нарисовала и пошла вновь вверх вплоть до уровня 61.8. Эти уровни очень примерны, и вы должны понимать, что цена не обязана отталкиваться от линий, которые вы нарисовали, и тут же отскочить. Уровни Фибоначчи – это именно уровни, а не линии.

Цена достигла уровня 61.8% и нарисовала пин-бар:

А потом вновь двинулась вниз и рисовала новые минимумы. При достижении нового минимума мы можем перетягивать нашу сетку ниже:

И как раз можно увидеть, что цена не дотянула до уровня 38.2 и ушла вниз:

Уровни Фибо отрабатываются не всегда

Но так или иначе их следует принимать во внимание, потому что очень часто они играют хорошую вспомогательную роль. Это всё касается уровней коррекции

Золотое сечение в науке код

Общее сопротивление этой бесконечной цепи равно Фr.

Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке, имеет общее сопротивление (между двумя левыми концами) Ф·r.

Отношение амплитуд колебаний и частот ~ Ф.

Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок).

Полностью эти две задачи рассматриваются в книге «В поисках пятого порядка», глава «Две простые задачки». Более сложные примеры на механические колебания и их обобщения рассматриваются в этой же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, физиологии.

Золотое сечение сильно связано с симметрией пятого порядка, наиболее известными трехмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию.
Молекула воды, у которой угол расхождения связей Н-О равен 104.7 , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н+(Н₂0)₂₁, который представляет из себя ион Н₃0+, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды.

Золотое сечение и гармония в искусстве код

Золотое сечение и зрительные центры

Некоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:

• Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
• Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 4:3 или 16:9) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»[источник не указан 3761 день].
• Следует отметить, что сама пропорция является, скорее, эталонным значением, матрицей, отклонения от которой у биологических видов, возможно, вызваны приспособлением к окружающей среде в процессе жизни. Примером таких «отклонений» может служить морская камбала.

Один из типов мозаики Пенроуза

Примеры сознательного использования | код

Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах.
Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)[источник не указан 986 дней].

Современными примерами применения золотого сечения может служить мозаика Пенроуза и пропорции государственного флага Того.

Литература

• Дональд Кнут. Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol. 1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4.
• Дональд Кнут, Роналд Грэхем, Орен Паташник. Конкретная математика. Основание информатики = Concrete Mathematics. A Foundation for Computer Science. — М.: Мир; Бином. Лаборатория знаний, 2006. — С. 703. — ISBN 5-94774-560-7.
• Грант Аракелян. Математика и история золотого сечения. — М.: Логос, 2014. — С. 404. — ISBN 978-5-98704-663-0.
• Ball, Keith M (2003), 8: Fibonacci’s Rabbits Revisited, Strange Curves, Counting Rabbits, and Other Mathematical Explorations, Princeton, NJ: Princeton University Press, ISBN 978-0-691-11321-0.
• Beck, Matthias & Geoghegan, Ross (2010), The Art of Proof: Basic Training for Deeper Mathematics, New York: Springer, ISBN 978-1-4419-7022-0.
• Bóna, Miklós (2011), A Walk Through Combinatorics (3rd ed.), New Jersey: World Scientific, ISBN 978-981-4335-23-2
  Тайны вселенной

  Bóna, Miklós (2016), A Walk Through Combinatorics (4th Revised ed.), New Jersey: World Scientific, ISBN 978-981-3148-84-0 .

  .

• Lemmermeyer, Franz (2000), Reciprocity Laws: From Euler to Eisenstein, Springer Monographs in Mathematics, New York: Springer, ISBN 978-3-540-66957-9.
• Lucas, Édouard (1891), , vol. 1, Paris: Gauthier-Villars,  в «Книгах Google».
• Pisano, Leonardo (2002), Fibonacci’s Liber Abaci: A Translation into Modern English of the Book of Calculation, Sources and Studies in the History of Mathematics and Physical Sciences, Springer, ISBN 978-0-387-95419-6

Загадка Леонардо

Одним из великих математиков, оказавших большое техническое и культурное влияние на среду рынков Форекс, стал средневековый математик Леонардо Фибоначчи. За его авторством была сформулирована последовательность чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и далее. Примечательность данного ряда состоит в том, что любое число из данного последовательности равно сумме предыдущих двух чисел. А после деления каждого числа из последовательности на число предыдущее получится соотношение равное — 1,618. Это наблюдение получило известность как “Золотое сечение”. А само название стало нарицательным для многих объектов человеческой жизнедеятельности, представляющих собой максимально приближенный к идеалу сплав положительных характеристик.

Неудивительно, что в честь одного из величайших математиков своего времени, была назван один из самых популярных и доходных индикаторов мира Форекс – уровни Фибоначчи. Который является основным элементом прекрасной торговой стратегии, регулярно получающей массу положительных отзывов и обрастающей новыми последователями.

Является ли стратегия торговли по уровням Фибоначчи тем самым золотым сечением? Попробуем разобраться.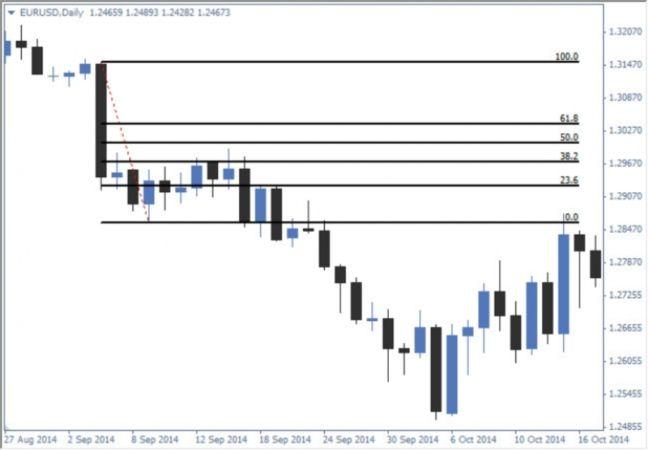

Математические свойства

• Φ{\displaystyle \Phi } — иррациональное алгебраическое число, положительное решение квадратного уравнения x2−x−1={\displaystyle x^{2}-x-1=0}, откуда, в частности, следуют соотношения:

  Φ2−Φ=1,{\displaystyle \Phi ^{2}-\Phi =1,}

  Φ⋅(Φ−1)=1.{\displaystyle \Phi \cdot (\Phi -1)=1.}

• Для чисел Φ{\displaystyle \Phi } и φ=1Φ{\displaystyle \varphi ={\frac {1}{\Phi }}} верны следующие равенства:
  • ΦΦ⋅φφ=Φ{\displaystyle \Phi ^{\Phi }\cdot \varphi ^{\varphi }=\Phi }
  • Φφ⋅φΦ=φ{\displaystyle \Phi ^{\varphi }\cdot \varphi ^{\Phi }=\varphi }

• Φ{\displaystyle \Phi } — представляется еще через тригонометрические функции:
  • Φ=2cos⁡π5=2cos⁡36∘.{\displaystyle \Phi =2\cos {\frac {\pi }{5}}=2\cos 36^{\circ }.}
  • Φ=2sin⁡(3π10)=2sin⁡54∘.{\displaystyle \Phi =2\sin(3\pi /10)=2\sin 54^{\circ }.}

1Φ=φ=tg⁡(arctg⁡(2)2)=21+1+22=21+5=5−12.{\displaystyle {\frac {1}{\Phi }}=\varphi =\operatorname {tg} \left({\frac {\operatorname {arctg} (2)}{2}}\right)={\frac {2}{1+{\sqrt {1+2^{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}

• Φ{\displaystyle \Phi } представляется в виде бесконечной цепочки квадратных корней:

  Φ=1+1+1+1+….{\displaystyle \Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}

• Φ{\displaystyle \Phi \;} представляется в виде бесконечной цепной дроби

  Φ=1+11+11+11+…,{\displaystyle \Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}

подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом,

• Φ=limn→∞Fn+1Fn.{\displaystyle \Phi =\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}.}

• Мера иррациональности Φ{\displaystyle \Phi } равна 2.

Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения

Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ=a/b{\displaystyle \Phi =a/b}, что и у исходного прямоугольника Φ=(a+b)/a{\displaystyle \Phi =(a+b)/a}.

Золотое сечение в пятиконечной звезде

В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.

Построение золотого сечения

Геометрическое построение. Золотое сечение отрезка AB{\displaystyle AB} можно построить следующим образом: в точке B{\displaystyle B} восстанавливают перпендикуляр к AB{\displaystyle AB}, откладывают на нём отрезок BC{\displaystyle BC}, равный половине AB{\displaystyle AB}, на отрезке AC{\displaystyle AC} откладывают отрезок CD{\displaystyle CD}, равный BC{\displaystyle BC}, и наконец, на отрезке AB{\displaystyle AB} откладывают отрезок AE{\displaystyle AE}, равный AD{\displaystyle AD}. Тогда

Φ=|AB||AE|=|AE||BE|.{\displaystyle \Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.}

Другой способ построить отрезок, равный по длине числу золотого сечения

Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=52{\displaystyle {\frac {\sqrt {5}}{2}}}. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны АD (точкой пересечения дуги и продолжения стороны АD пусть будет точка Н). Как радиусы круга BE=СЕ=ЕН. Так как АН=АЕ+ЕН, результатом будет отрезок АН длиной Φ{\displaystyle \Phi }. Так как DH=EH-ED, другим результатом будет отрезок DH длиной φ{\displaystyle \varphi }.

• Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
• Значения дроби после запятой для Φ{\displaystyle \Phi }, 1Φ{\displaystyle {\frac {1}{\Phi }}} и Φ2{\displaystyle \Phi ^{2}} в любой системе счисления будут равны.
• ∑n=1∞(−1)n+1n2(2nn)=2ln2⁡φ{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{2}{\binom {2n}{n}}}}=2\ln ^{2}\varphi }

Тогда как ∑n=1∞1n2(2nn)=π218{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}}[источник не указан 1393 дня]

Что такое расширение Фибоначчи?

Расширение Фибоначчи – это две разнонаправленные трендовые линии, соединенные вместе и связанные с уровнями Фибоначчи, берущими отсчет от 61,8%.

В стандартной интерпретации этого инструмента на множестве торговых платформ, в том числе Metatrader, таких уровней реализовано три: 61.8, 100, 161.8.  Числовой выбор объясняется областью применения инструмента:

Расширение Фибоначчи представляет собой две волны Эллиотта, как правило, I и II, с целью найти точки коррекции на третьем, самом протяженном по длине, движении тренда.

Применение инструмента предусматривает, что начало волны II выше волны I при восходящем тренде и ниже при нисходящем движении.

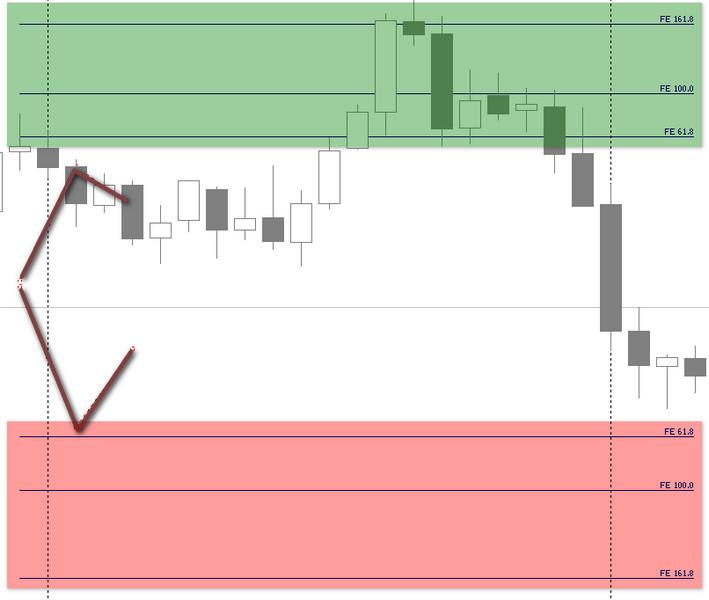Некоторые трейдеры-волновики универсально используют расширение Фибоначчи, располагая его в конце второй волны ниже первой на восходящем тренде, и наоборот — при нисходящем, чтобы подтверждать вершины/впадины коррекционных трех волн ABC.

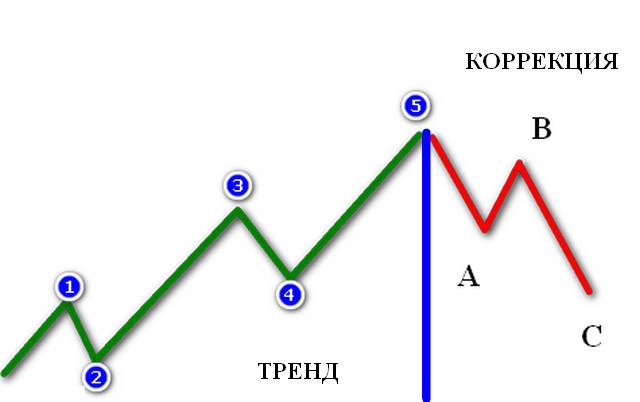В обычных волнах Фибоначчи трейдер рассматривает лишь одно трендовое движение, чтобы поймать момент входа на коррекции, представленный, как минимум, тремя уровнями 38,2%, 50% и 61,8%, иногда к ним добавляют 23,8%, «работающий» на сильном, импульсном тренде. Уровни отлично отрабатываются в случае резкого направленного изменения курса валютной пары.

Цифра 61.8% – сигнал для прекращения попыток войти по тренду, указывающий, что он «сломан» такой глубиной коррекции. Поэтому логично, что эта линия выбрана, как первый тейк-профит в расширении Фибоначчи. Работа этого инструмента проходит на уже сложившемся паттерне тренда – это и есть основное отличие между уровнями и расширением:

• Линии Фибоначчи показывают точки входа на развороте по тренду;
• Расширения Фибоначчи прогнозируют точки выхода с прибылью при продолжении тренда.

Охотимся за золотом

Переходим к непосредственной торговле

Здесь важно выбрать подходящую валютную пару. Самой распространенной из них является GBP/USD

Именно на этом активе чаще всего происходит отскок на нашем показателе в 23,6 процента. Отдавая предпочтение стабильному заработку, вам стоит рассмотреть модель консервативного поведения, согласно которой лучше всего открываться на отскок от уровня именно 38,2 % с фиксацией прибыли на уровне 23,6 %. Многие опытные трейдеру используя стратегии родственные нашей, проводят свои сделки от отметки в 38,2 %.

Часто продолжение движения после отскока от уровня 38,2% не заканчивается и дальше уровня 23,6 %, поэтому у нас остается возможность увеличивать нашу цель. Ставить момент фиксации прибыли, так называемый “тейк-профит” в этом случае можно либо на отметке 23,6 %, либо на нулевом показателе. Не стесняйтесь вести себя скромно и взять прибыль на уровне 23,6 %. Долго в рынке находиться не стоит. Помните, что риски коррелирует со временем открытой позиции. Во всех открываемых сделках показатель потенциальных убытков — стоп-лосс рекомендовано располагать за отметку 61.8 %.

Золотое сечение и гармония в искусстве

Золотое сечение и зрительные центры

Некоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:

• Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
• Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 4:3 или 16:9) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»[источник не указан 4009 дней].
• Следует отметить, что сама пропорция является, скорее, эталонным значением, матрицей, отклонения от которой у биологических видов, возможно, вызваны приспособлением к окружающей среде в процессе жизни. Примером таких «отклонений» может служить морская камбала.

Один из типов мозаики Пенроуза

Примеры сознательного использования

Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах.
Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)[источник не указан 1234 дня].

Современными примерами применения золотого сечения может служить мозаика Пенроуза и пропорции государственного флага Того.

Расширения Фибоначчи

Но у нас также имеется инструмент, который называется Расширения Фибоначчи, использующий тот же принцип, что и уровни, полученные из ряда чисел, открытых великим математиком. «Магию» их цифр легко объяснить с точки зрения психологии подсознательных рефлексов трейдеров на движение цены, если представить значения в процентном ряде: 23,8%, 38,2 и т.д.

Именно в этих точках, относительно пропорции (размаха) предыдущего движения актива, большинство трейдеров видит развороты, как возможность для входа, дополнительного входа или цели усреднения пирамиды ордеров, выставляемых в надежде на продолжение тренда, чтобы:

• Увеличить прибыль уже существующей сделки;
• Скорректировать преждевременный вход, «понизить» общую цену или войти по более привлекательному курсу, закрыв первую сделку «в ноль» при возврате движения к тренду.

Правоту предположения, что все трейдеры выбирают одинаковые уровни, исходя из психологии и процентного соотношения, доказал Эллиотт. Именно он открыл преобразование числового ряда Фибоначчи в процентные пропорции уровней, исходя из многочисленных наблюдений и расчетов, из которых возникла знаменитая «Волновая теория».

Без чисел математика было бы невозможно открыть пяти-волновую структуру и три волны коррекции, определить точки их отсчета и разворота. Расширение Фибоначчи – это инструмент, упрощающий задачу расчета и поиска паттернов Эллиотта.

Золотая спираль Фибоначчи

Это спираль, которая выглядит следующим образом:

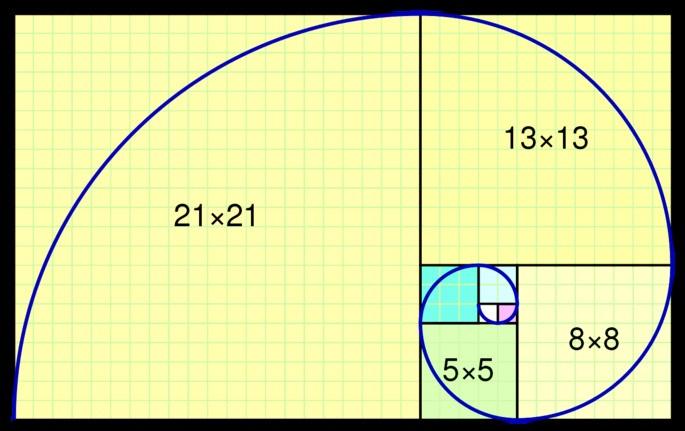Числа Фибоначчи — последовательность чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

Как можно видеть на изображении, тут представлен числовой ряд Фибоначчи как спираль. Она начинается в центре с двух квадратов 1×1, за ними следуют квадраты 2×2, 3×3, 5×5 и так далее.

Числа Фибоначчи в природе

Фотография «Алоэ многолистное» (Aloe polyphylla), на фото можно увидеть спираль Фибоначчи в природе.

«Спираль ракушки», фотограф Muffett68 Heidi; ещё один пример спирали Фибоначчи в природе.

В этом видео «ЧИСЛА ФИБОНАЧЧИ УДИВИТЕЛЬНАЯ ЗАКОНОМЕРНОСТЬ» ещё больше примеров чисел Фибоначчи в природе и в мире вокруг нас.

Коэффициенты Фибоначчи

Из последовательности Фибоначчи выводится ряд коэффициентов имеющих особое значение для трейдеров.

Наиболее важным коэффициентом является отношение очередного члена последовательности к следующему члену. Это соотношение практически одинаково для любых двух последовательно идущих членов и стремится к величине 0,618 или 61,8%. Это соотношение называют «золотой серединой» или «золотым сечением». Золотое сечение также имеет широкое распространение в природе, в частности пропорции человеческого тела, очень близки к нему. В трейдинге значение 61,8% является наиболее надежным уровнем прогнозирования отката. Например:

8 разделить на 13 = 0,615 = 61,5%

13 разделить на 21 = 0,619 = 61,9%

21 разделить на 34 = 0.617 = 61,7%

Два других коэффициента Фибоначчи часто используемые трейдерами это 38,2% и 23,6%. Эти два коэффициента считаются менее надежными, но также применяются в техническом анализе.

Отношение 38,2% получают путем деления любого члена последовательности на число стоящее через один разряд вправо. Например:

8 делится на 21 = 0,380 = 38,0%

144 делится на 377 = 0,381 = 38,1%

6765 делится на 17 716 = 0,381 = 38,1%

Аналогичным образом, отношение 23,6% получается делением любого члена последовательности на число через два разряда вправо:

5 делится на 21 = 0,238 = 23,8%

34 разделить на 144 = 0,236 = 23,6%

6765 делится на 28 667 = 0,235 = 23,5%

Кликните по рисунку для увеличения

Примечания

1. ↑
2. Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
3. Boyer, Carl B. (англ.)русск.. A History of Mathematics (неопр.). — Second Edition. — John Wiley & Sons, Inc., 1991. — С. 50. — ISBN 0-471-54397-7.
4. , p. 168.
5. , p. 6-7.
6. , p. 169.
7. , p. 7.
8. , p. 169-170.
9. .
10. Ковалев А.Н. В поисках пятого порядка. — 2017. — 374 с. — ISBN 978-5-4485-3753-0.
11. Современная Кристаллография / под ред. Вайнштейна Б. К.. — Т.2. — М.: Мир, 1979.
12. Holland P. M. Casteiman A. W. A model for the formation and stabilization of chorqed water cluthrates // J. Chem. Phys.. — 1980. — Т. 72, № 1(11). — С. 5984.
13. Электромагнитные поля в биосфере. — Сборник трудов конференции, Т.2. — М., 1984. — С. 22.
14. Зенин С.В. Структурированное состояние воды как основа управления поведением и безопасностью живых систем. — Диссертация докт. биол. наук. — М., 1999.

Краткий вывод

Индикатор, названный в честь великого математика отлично проявляет себя на всех временных интервалах, но наиболее прибыльное использование замечается при работе с часовыми и 4-х часовыми графиками. В данном случае отведенное время на исполнение приказа невелико, так как вероятность неприятных новостей тоже крайне мала. Значимые процентные отметки Фибо при использовании их на дневных и недельных графиках Форекс-рынков помогут трейдеру определять потенциальные участки окончания корректировочных накатов. Большое количество опытнейших трейдеров формулируют свои личные стратегии на основе показателей Фибоначчи. Высокий процент точности и четкости сигналов может быть увеличен за счет сочетания с другими торговыми инструментами, например, с индикаторами типа MACD или RSI. Данные мероприятия существенно увеличивают общую доходность всего предприятия, а вкупе с личным опытом трейдера, его знаниями и разработанной интуицией, комбинация и вовсе может оказать взрывное воздействие на рост вашего депозита.