Множество мандельброта

Как пользоваться в терминале MT4 индикатором Вильямса – Fractals, разработанным на основе Фрактала Мандельброта?

Итак, описание индикатора мы рассмотрели, для чего его применяют, тоже знаем, теперь давайте узнаем, как пользоваться данным алгоритмом при торговле. Сразу отметим, что настройки индикатора в базовой комплектации МТ4, необходимо оставлять по умолчанию.

Индикатор Фрактал для МТ4 и 5 позволяет торговать любыми валютами даже со средней волатильностью, но при устойчивом тренде.

Рассмотрим, как пользоваться Фракталом без индикатора Аллигатор, который, как правило, всегда применяется трейдерами при использовании рассматриваемого нами алгоритма на примере – на графике D1, выполним анализ по открытию текущего дня.

Также, может пригодится и отдельно: скачать индикатор Fractals

При наличии фрактала вверх:

• открываем сделки на продажу,
• при нисходящем – на покупку.

Здесь можно открыться с рынка, а можно использовать отложенные ордера.

Так для покупок, ставим Buy Stop выше (от 2 до 4 пунктов) максимума второй по отношению к фрактальной свечи. Для продаж выставляем Sell Stop ниже (от 2 до 4 пунктов) минимума второй от фрактальной свечи. Как правило, стоп приказы при использовании данного варианта торговли не используются – сделки в конце дня закрывают вручную.

Если же Вы практикуете использование стоп приказов, то ставить их рекомендовано за уровнем фрактальной свечи.

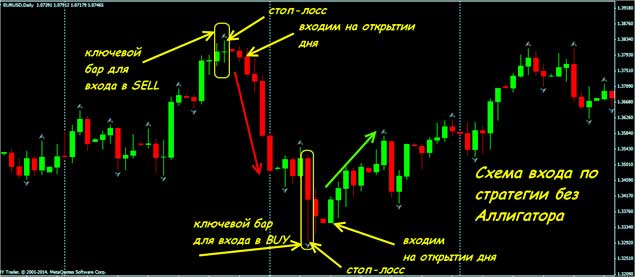
Конечно, на истории все просто и легко, но что же делать с запаздываниями, ведь для идентификации, а также подтверждения формации индикатор Фрактал требует, чтобы произошло закрытие двух свечей. Решение здесь простое – «дробление» временных промежутков.

Здесь трейдеру на помощь приходит нестандартный индикатор Фрактал – «MTF_Fractal». В процессе настройки данного алгоритма следует задать единственный параметр – таймфрейм.

Скачать MTF_Fractal для МТ4

Сразу необходимо обратить внимание, что временной формат указывается в минутах, то есть для отображения фракталов, к примеру, с Н4 на часовом графике, значение функции следует задать, как «240»

Помощник «m-Candles», для индикатора Вильямса — Фрактал (Fractals)

Помимо этого, для более эффективной торговли с фрактальным индикатором рекомендовано использовать алгоритм «m-Candles», выводящий на графики МТ4 и 5 свечи со старших таймфреймов:

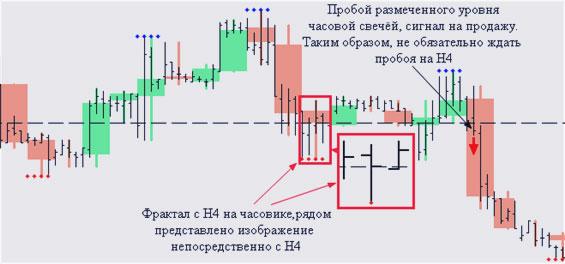
Так используя MTF_Fractal, Вы одновременно сокращаете потери от запаздывания и не распыляете свое внимание, так как вся необходимая информация находится в одном окне. Индикатор Фрактал в МТ4, разработанный по Фракталу Мандельброта

Описание и настройки

Индикатор Фрактал в МТ4, разработанный по Фракталу Мандельброта. Описание и настройки

ТОП БРОКЕРОВ, ПРИЗНАННЫХ НЕЗАВИСИМЫМИ РЕЙТИНГАМИ

*БО. Не требуется верификация! | обзор/отзывы | НАЧАТЬ ТОРГОВЛЮ С 10$
*БО. Выгодные условия. | обзор/отзывы | ПОПРОБОВАТЬ НА ДЕМО

_________________________________________________________________________

2007 год. FinaCom.   КЕШБЭК 16$ С ЛОТА! | обзор/отзывы
1998 год. FCA, НАУФОР. | х2 УМНОЖАЕМ БОНУСЫ | обзор/отзывы
2007 год. БОНУС $1500 НА СЧЕТ. |

Раскрашиваем изображение множества Мандельброта

В той же книге Седжвика и других авторов сформулирована следующая задача:
модернизировать программу построения изображения множества Мандельброта
таким образом, чтобы сделать его «цветным». Для этого предлагается
раскрашивать изображение не 256-ю оттенками серого, а 256-ю произвольными
цветами (среди которых, разумеется, могут быть и оттенки серого). Давайте
решим эту задачу.

Действовать будем следующим образом. Передавая комплексное число в
функцию get_gray_color(),
будем теперь рассматривать интенсивность серого цвета, возвращаемую
функцией, как номер цвета из некоторого предопределённого списка цветов.
Именно этим цветом и будем раскрашивать пиксель, соответствующий данному
комплексному числу.

Очевидно, что изменять функцию get_gray_color()
не требуется. А вот функцию main()
нужно переделать. Вот её новая, «цветная» версия:

 1.int main()
 2.{
 3.    uchar red[] = {, 36, 73, 109, 146, 182, 219, 255};
 4.    uchar *green = red;
 5.    uchar blue[] = {, 85, 170, 255};
 6.    color colors;
 7.    int m = ;
 8.    for (int i = ; i < 8; i++)
 9.        for (int j = ; j < 8; j++)
10.            for (int k = ; k < 4; k++)
11.                colors = (color) {red, green, blue};
12.    image *img = create_image(W, H);
13.    for (int i = ; i < W; i++)
14.        for (int j = ; j < H; j++)
15.        {
16.            double x = (i - X0) / L;
17.            double y = (j - Y0) / L;
18.            double complex z = x + I * y;
19.            uchar num = get_gray_color(z);
20.            if (num != 255)
21.                set_color(img, i, j, colors);
22.        }
23.    save_to_file(img, "out.bmp");
24.    free(img);
25.    return ;
26.}

Список предопределённых цветов, о котором шла речь выше, формируется в
виде массива colors в
строках 3-11. Принцип формирования достаточно простой: выбираются по 8
оттенков красного и зелёного цветов, а также 4 оттенка синего. Далее эти
оттенки смешиваются, в результате чего получаются 256 цветов, коими и
заполняется массив colors
посредством трёх вложенных циклов (см. стр. 7-11). Интенсивности каждого
из трёх цветов примерно равномерно распределяются по спектру
интенсивностей данного цвета (см. стр. 3-5).

Теперь значение, возвращаемое функцией get_gray_color(),
интерпретируем как индекс элемента массива colors,
содержащего цвет, которым нужно раскрасить текущий пиксель (см. стр.
19-21). Заметим, что значениям 0 и 1, возвращаемым функцией, как и в
предыдущем («чёрно-белом») случае, соответствуют чёрный и белый цвета
пикселя соответственно.

В результате выполнения новой версии программы получаем следующее
изображение:

Цветное изображение множества Мандельброта

Ясно, что существует огромное количество способов раскраски множества
Мандельброта. Для получения некоторых из них можно, например, изменить
порядок следования выражений внутри фигурных скобок, отвечающих за
значения полей элементов массива colors
(см. стр. 11). Существуют, очевидно, 6 вариантов расположения выражений:

1.                colors = (color) {red, green, blue};
2.                colors = (color) {red, blue, green};
3.                colors = (color) {blue, red, green};
4.                colors = (color) {green, blue, red};
5.                colors = (color) {blue, green, red};
6.                colors = (color) {green, red, blue};

Заменяя 11-ю строку функции main()
одной из приведённых выше строк (за исключением 1-й), получаем ещё 5
вариантов раскраски. Изображения множества Мандельброта, раскрашенного
всеми 6-ю способами, соответствующими 6-ю приведённым выше строкам,
изображены ниже.

6 изображений множества Мандельброта (щёлкните для увеличения)

#define W 1281
#define H 1281
#define X0 (3*W/4)
#define Y0 (H/2)
#define L 640.0

В качестве 11-й строки (см. код функции main())
будем использовать следующую:

                colors = (color) {red, blue, green};

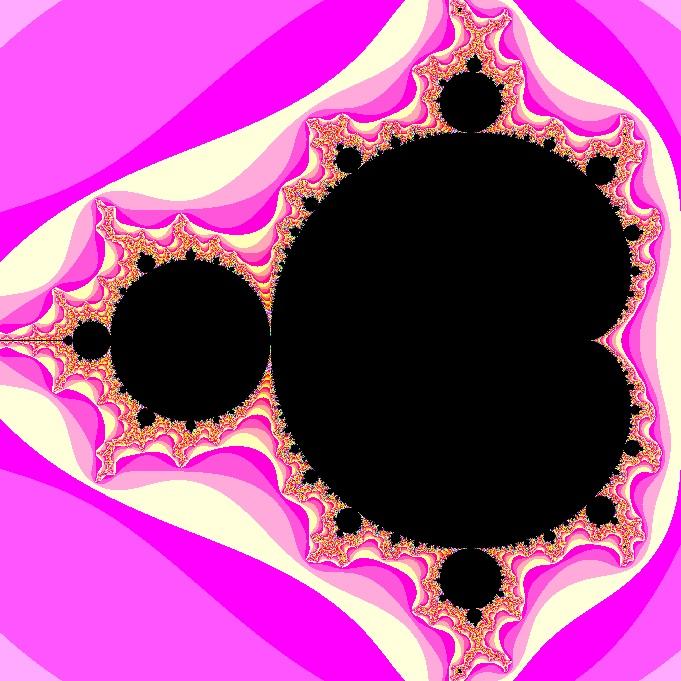
Ещё одно изображение множества Мандельброта (щёлкните для увеличения)

И последнее. Из алгоритма раскраски множества Мандельброта следует, что
раскраске подвергаются лишь пиксели, соответствующие точкам комплексной
плоскости, удалённым от начала координат не более, чем на 2, т. е.
лежащими внутри круга радиуса 2 с центром в начале координат или на его
границе. Давайте рассмотрим этот круг полностью. Для этого изменим
значения макросов, определённых в файле main.c следующим образом:

#define W 1281
#define H 1281
#define X0 (W/2)
#define Y0 (H/2)
#define L 320.0

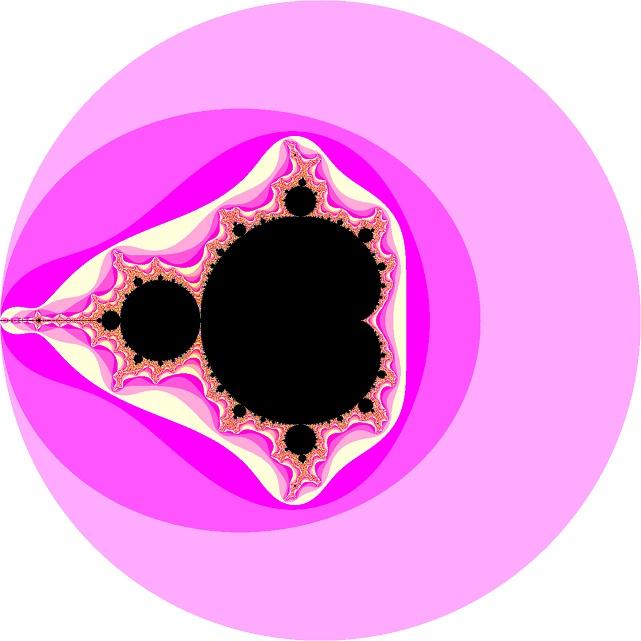
Множество Мандельброта с высоты птичьего полёта (щёлкните для
увеличения)

Применение множества Мандельброта

Множество Мандельброта находит применение для анализа возникновения турбулентности в физике плазмы и термодинамике, развития бифуркаций и т. д.[источник не указан 601 день]

Применение в искусстве

Поиск красивых фрагментов цветных версий множества Мандельброта — интересное хобби для очень многих людей. Они собирают коллекции таких изображений, причём каждое из них может быть описано небольшим количеством параметров, например, просто координатами центра. Элементом творчества является не только поиск координат, но и подбор таблицы цветов, связывание её с количеством выполненных итераций, а также максимально число выполняемых итераций.

Есть большое количество программ для рисования фракталов, но, несмотря на это, многие люди пишут свои программы для большей гибкости при экспериментах. Например, эти анимированные изображения были созданы таким способом.

Отец фракталов

Вплоть до 20 века шло накопление данных о таких странных объектах, без какой либо попытки их систематизировать. Так было, пока за них не взялся Бенуа Мандельброт — отец современной фрактальной геометрии и слова фрактал. Работая в IBM математическим аналитиком, он изучал шумы в электронных схемах, которые невозможно было описать с помощью статистики. Постепенно сопоставив факты, он пришел к открытию нового направления в математике — фрактальной геометрии.

Что же такое фрактал. Сам Мандельброт вывел слово fractal от латинского слова fractus, что означает разбитый (поделенный на части). И одно из определений фрактала — это геометрическая фигура, состоящая из частей и которая может быть поделена на части, каждая из которых будет представлять уменьшенную копию целого (по крайней мере, приблизительно).

Чтобы представить себе фрактал понаглядней рассмотрим пример, приведенный в книге Б.Мандельброта «The Fractal Geometry of Nature» («Фрактальная геометрия природы») ставший классическим — «Какова длина берега Британии?». Ответ на этот вопрос не так прост, как кажется. Все зависит от длины инструмента, которым мы будем пользоваться. Померив берег с помощью километровой линейки мы получим какую-то длину. Однако мы пропустим много небольших заливчиков и полуостровков, которые по размеру намного меньше нашей линейки. Уменьшив размер линейки до, скажем, 1 метра — мы учтем эти детали ландшафта, и, соответственно длина берега станет больше. Пойдем дальше и измерим длину берега с помощью миллиметровой линейки, мы тут учтем детали, которые больше миллиметра, длина будет еще больше. В итоге ответ на такой, казалось бы, простой вопрос может поставить в тупик кого угодно — длина берега Британии бесконечна.

Дырявый треугольник

Что же такое фрактал? Так как строгого математического определения для этого объекта, вообще говоря, не существует, то удобно будет начать объяснение с примера.

В 1916 году польский математик Вацлав Серпинский опубликовал работу, в которой предложил следующую геометрическую конструкцию. На первом этапе автор брал равносторонний треугольник и выкидывал из него треугольник, полученный путем соединения середин сторон исходного. Получалась фигура, составленная из трех треугольников, площадь каждого из которых составляла четверть от площади исходного треугольника. На втором этапе аналогичная операция проделывалась с оставшимися треугольниками.

Продолжая действовать по этой схеме, Серпинский получил последовательность фигур, пределом которой является очень «дырявый» треугольник. Это и есть фрактал, получивший название треугольника Серпинского. Данный объект обладает рядом удивительных свойств. Например, его площадь (мера Лебега, если быть точным) равна нулю, а отдельные куски, будучи увеличенными, оказываются такими же, как исходная фигура.

Последнее свойство — самоподобие — часто берут за основу определения фрактала. То есть фрактал — это фигура, обладающая некоторой степенью самоподобия. Другим, более экзотическим, является определение фрактала как топологического пространства дробной хаусдорфовой размерности. Например, размерность треугольника Серпинского равна log 3/log 2, то есть не является целым числом.

Множество Мандельброта

Вместе с тем треугольник Серпинского, как и большинство классических фракталов, плохо поддается визуализации. Максимум, чего можно добиться от этой конструкции — нарисовать несколько фигур, входящих в последовательность.

Понимал это и Бенуа Мандельброт, поэтому и стал искать для своей книги другие фракталы. Бенуа повезло и главную звезду своей книги, позже получившую имя «множество Мандельброта», он обнаружил в работах своего учителя Жулиа.

Для того чтобы понять, что иллюстрирует множество Мандельброта, нам потребуются комплексные числа. Через i будем обозначать мнимую единицу, обладающей свойством i2 = -1. Комплексным числом называется выражение вида a + i b. Эти числа можно складывать (как многочлены), умножать (раскрывая скобки по правилу умножения многочленов с учетом тождества i2 = -1), делить, извлекать корни и так далее — в общем, делать все, что можно делать с обычными (действительными) числами.

Каждое комплексное число можно представлять себе точкой на плоскости, задаваемой координатами (a, b). В свою очередь, любая функция комплексной переменной, скажем, возведение в квадрат, задает отображение плоскости в себя — каждой точке-аргументу ставится в соответствие точка-значение функции на данном аргументе. Например, возведем число 1 + i в квадрат: (1 + i)2 = 1 + 2i + i2 = 1 + 2i — 1 = 2i. Стало быть, если возведение в квадрат рассматривать в качестве отображения, то соответствующая первому числу точка (1, 1) переходит в точку (0, 2), соответствующую результату возведения в квадрат.

Оказывается, точек на плоскости недостаточно для изучения отображений, так как, например, функция 1/z в нуле не определена, то есть соответствующее отображение просто «не знает», куда переводить ноль. Поэтому плоскость дополняют одной бесконечной точкой, получая в результате сферу Римана.

Именно отображения сферы Римана в себя рассматривали Жулиа и Фату. Их интересовал вопрос, как ведет себя точка O с координатами (0, 0) при многократном применении к нему отображения? В качестве простейшего примера Мандельброт взял отображение f(z) = z2 + c, где c — некоторая постоянная. Если она равна нулю, ноль остается на месте. Если же c отлично от нуля, то судьба O, вообще говоря, не ясна — точка может начать «убегать» на бесконечность. Будем отмечать на плоскости такие точки c, что при этих значениях параметра точка O на бесконечность не убегает. Что это получится за множество? Оказывается, получится самоподобная фигура, устроенная довольно сложным образом.

Бенуа Мандельброт не удовлетворился описательным ответом, который содержался в работах Жулиа. Вместо этого он заставил компьютер нарисовать загадочный объект. Именно этот шаг, простой и естественный с точки зрения современного пользователя, произвел в 1977 году настоящий фурор. Сложные загадочные объекты, которые считались уделом сухой теории, на картинках оказались поистине завораживающими.

После «Фрактальной геометрии природы» Мандельброт выпустил еще много книг, в том числе и серьезных научных работ, стал лауреатом десятков престижнейших премий. Однако в сердцах тысяч людей по всему миру он останется тем первопроходцем, который открыл простым людям завораживающую красоту математики.

О множестве Мандельброта

Множество Мандельброта, как и рассматривавшиеся ранее
бассейны Ньютона, относится к фракталам — множествам, обладающим свойством
самоподобия. Это свойство заключается в том, что множество может быть
разбито на части, каждая из которых имеет структуру, совпадающую со
структурой исходного множество (или близкую к структуре исходного
множества), причём разбиения одних частей на другие части,
«воспроизводящие» (в той или иной степени) исходные, могут быть продолжены
до бесконечности.

Множество Мандельброта, помимо различных ценных свойств, интересно ещё и
тем, что может иметь весьма привлекательные с эстетической точки зрения
визуализации. Некоторые из визуализаций мы построим с помощью нашей
будущей программы.

Пред тем, как переходить к визуализации, дадим определение множества
Мандельброта.

Рассмотрим, вначале, произвольное комплексное число z = x + iy.
Этому числу соответствует точка на комплексной плоскости с координатами (x, y).
В дальнейшем будем отождествлять комплексные числа с соответствующими им
точками комплексной плоскости. Комплексную последовательность

z, z₁,
z₂, …, где z_k = (z_k-1)2
+ z, k ∈ ℕ,

назовём, последовательностью Мандельброта для точки z.
Ясно, что каждая такая последовательность является либо ограниченной (по
модулю, разумеется), либо неограниченной. Множеством Мандельброта
называется множество всех таких точек комплексной плоскости, для которых
последовательности Мандельброта ограничены.

Простейшая визуализация множества Мандельброта заключается в следующем.
Точкам некоторой прямоугольной области комплексной плоскости естественным
образом ставятся в соответствие пиксели холста для рисования. Пиксели,
соответствующие точкам плоскости, принадлежащим множеству Мандельброта,
закрашиваются чёрным цветом, а остальные — белым. Кстати,
известно, что точки множества Мандельброта более или менее «помещаются» в
квадрат с центром в точке (-1/2, 0) со стороной 2.

Для построения такой визуализации, очевидно, требуется алгоритм,
устанавливающий принадлежность или непринадлежность той или иной точки
комплексной плоскости множеству Мандельброта. Проблема заключается в том,
что универсального алгоритма, «работающего» для любой точки, не
существует. Однако известно, что последовательность Мандельброта, модуль
некоторого члена которой превышает 2, стремится по модулю к бесконечности,
т. е. не ограничена. Это означает, что начальный член этой
последовательности не принадлежит множеству Мандельброта.

Это утверждение позволяет нам использовать алгоритм определения
«условной» принадлежности точки данному множеству. Заключается он в
вычислении фиксированного, заранее выбранного числа первых членов
последовательности Мандельброта для проверяемой точки. Если модуль ни
одного из вычисленных членов не превосходит числа 2, то испытуемая точка
считается принадлежащей множеству Мандельброта. В противном случае точка
считается этому множеству не принадлежащей.

Авторы упомянутой ранее книги предлагают ограничиться нахождением первых
255 членов последовательности (включая саму проверяемую точку). Если все
255 чисел оказываются по модулю не превосходящими 2, то соответствующие им
пиксели окрашиваются в чёрный цвет. Если же начальный член (т. е. сама
проверяемая точка) превосходит по модулю 2, то соответствующий ей пиксель
закрашивается в белый цвет.

Если же установлена непринадлежность точки z
множеству Мандельброта по причине того, что для некоторого минимального k
такого, что 1 ≤ k ≤ 254, выполняется
неравенство |z_k| > 2, то в этом случае
логично окрашивать соответствующий точке пиксель также в белый цвет.
Однако авторы книги предлагают иной подход: закрашивать пиксель оттенком
серого цвета. При этом цвет закраски должен быть тем ближе к белому, чем
меньше k и тем ближе к чёрному, чем больше k. Более
конкретно: интенсивность серого цвета предлагается вычислять как разность
255 − k.

В данном случае имеется в виду интенсивность, которая совпадает со
значениями каждой из трёх компонент при сохранении цветов в RGB-формате.
Напомним, что каждому оттенку серого соответствует именно совпадение
компонент.

Таким образом, наша «картинка» не будет содержать лишь два цвета: черный
и белый. Но будет включать в себя и точки серого оттенка, тем более
тёмные, чем «позже» члены последовательностей Мандельброта для этих точек
превосходят по модулю число 2.

Как мы видим, алгоритм раскраски весьма прост; пожалуй, даже, не
требуется формулировать его в строгом виде, а можно уже переходить к
построению программы.

Математические факты о множестве Мандельброта

Давди и Хаббард доказали, что множество Мандельброта является связным, хотя в это и трудно поверить, глядя на хитрые системы мостов, соединяющие различные его части. Связность множества Мандельброта следует из того, что оно является пересечением вложенных связных компактных множеств.

Однако неизвестно, является ли оно локально связным. Эта известная гипотеза в комплексной динамике получила название MLC (англ. Mandelbrot locally connected). Многие математики прилагают усилия к её доказательству. Жан-Кристоф Иокко (Jean-Christophe Yoccoz) доказал, что гипотеза верна во всех точках с конечной ренормализацией, затем многие другие математики доказывали справедливость гипотезы во многих отдельных точках множества Мандельброта, но общая гипотеза остается недоказанной.

Мицухиро Шишикура (Mitsuhiro Shishikura) доказал, что размерность Хаусдорфа границы множества Мандельброта равна 2. Но остается неизвестным ответ на вопрос, имеет ли граница множества Мандельброта положительную меру Лебега на плоскости.

Число итераций для любой точки в построении множества очень близко к логарифму электрического потенциала, который возникает, если зарядить множество Мандельброта. Точнее, предел ln⁡(ln⁡(|zn|)2n)+const{\displaystyle \ln {\big (}\ln(|z_{n}|)/2^{n}{\big )}+{\text{const}}} совпадает с этим потенциалом.

Подведем итоги

Если быть честным, то я редко пользуюсь фракталами, но в начале своего пути я их использовал. Мне они помогали в плане выставления страховочных ордеров, тейк-профитов. Чаще всего они мне были нужны в выставлении разметки горизонтальных уровней. К примеру, если я видел, что максимальные или минимальные значения, которые выражены с помощью фракталов находились примерно на одном уровне, то они сразу же бросались в глаза и я проводил по ним уровень. В дальнейшем такие уровни использовались мной в качестве отличных точек, как для входа в позицию, так и для выхода из нее.

В одно время, два очень серьезных трейдера, я бы сказал даже рыночных «гуру» поспорили, даже не то, чтобы поспорили, а решили провести очень занимательный эксперимент, который заключался в том, чтобы научить людей далеких от биржи спекуляциям. Немного посовещавшись, наши «гуру» решили взять себе по десять человек и дали объявление в газету, так как их имена были на слуху, то желающих появилось огромнейшее количество.

Экспериментаторы начали очень крупулезный отбор, так как чья команда бы показала лучший результат, тот бы из гуру и выиграл. Спустя некоторое время, люди были найдены и «учителя» перешли к следующему этапу, они взяли одну и ту же торговую стратегию, с конкретными правилами входа в рынок и выхода из него, по сути дела, если следовать логике, то результат должен был получиться приблизительно одинаковым. Согласитесь, все очень логично, одна стратегия, одни правила, равные капиталы для торговли….

Но по истечению года торговли, при подведении результатов, итоги получились совершенно различные, как Вы думаете, чем это объяснялось? Дело в том, что каждый человек по своему уникален и как следствие, видение рынка тоже является уникальным. К примеру, где один трейдер четко заходил по системе и произведенному сигналу, второй трейдер его мог просто не увидеть или же засомневаться и пропустить сделку…. Понимаете о чем я?

По каким критериям лично для себя я отбираю лучшие индикаторы, вообще, первое — это конечно же понимание инструмента, Вы должны четко понимать, когда индикатор подает сигнал на покупку, когда на продажу, а когда лучше вообще воздержаться от сделок, у Вас не должно быть сомнений, есть или нет сигнал, если он есть, Вы должны молниеносно понимать, что да, это сигнал для открытия позиции, а если его нет, не сомневаться и не гадать на «кофейной гуще», есть ли здесь сигнал или нет.

Второй признак, по которым я отбираю лучший индикатор для себя — это конечно же мои торговые результаты, помимо основной торговли, которая к слову сказано проходит в среднесрочном режиме, я занимаюсь тестирование различных торговых стратегий, к примеру, если я обкатываю что-то новое, ранее мне неизвестное, то я просто провожу 30-50 сделок по сигналам системы и смотрю на свой результат, после чего сравниваю его с предыдущими, вот такие очень простые, но очень эффективные советы.

Ну и напоследок давайте я дам еще один очень действенный совет, многие из Вас находятся сейчас именно на стадии поиска «Святого Грааля», среди трейдеров этап поиска чудодейственного индикатора называется именно так. Как бы так ам попроще объяснить, понимаете такие поиски Вас ни к чему не приведут, прибыльно торговать можно даже с помощью одной простой скользящей средней, все дело в управлении рисками, управлении позицией, мани менеджменте.

Не так давно я наткнулся на одну очень интересную статистику, которая состояла из миллиона случайно отобранных трейдеров. Самое интересное заключалось в том, что у «львиной» доли трейдеров, процент прибыльных сделок, находился выше процента убыточных, но при этом их конечных результаты были в глубоком минусе. Понимаете, все дело в управлении рисками и давайте я постараюсь Вам разжувать.

Таким образом, я склоняю вероятность в свою сторону, предположим, что моя ставка идет по 100 долларов, любая сделка в перспективе может принести мне 200 долларов, если посмотреть далеко вперед, скажем на 100 сделок то у нас будет получаться следующая картина. Предположим, что я выигрываю всего сорок из ста, мой убыток после ста сделок будет составлять 6000 долларов, а прибыль 8000 долларов, при этом, даже при условии что я проигрываю больше, чем выигрываю, я все равно остаюсь в плюсе на 2000 долларов, а моя статистика находится в районе 65-70% успешных ордеров и мне этого вполне хватает, подумайте хорошенько над этим и хватит уже искать «грааль», которого не существует)))

Подведем итоги

Сегодня мы окунулись в фрактальную теорию, буду с Вам честен и откровенен, я не фанат торговли по фракталам, предпочитаю другие инструменты для спекуляций, но все же отмечу, что фракталы довольно интересная тема. Лично я бы посоветовал прочитать книгу Билла Вильямса, «Новые измерения биржевой торговли», в ней более подробно рассмотрено ся фрактальная теория, а так же разработана конкретная стратегия фрактальной торговли при использования индикатора Аллигатор.

Я читал данную книгу и она написана довольно интересно и увлекательно, но лично мне не подходит такой вид торговли

Кроме самой системы торговли, Билл открывает то, что по настоящему движет ценой, а так же обращает внимание на те моменты, которые практически никем не были затронуты

Ну а по индикатору «Фрактал» мы поставим оценку 4- из 5