Метр

История Править

Международный эталон метра, использовавшийся с по 1960 годы.

ФранцииXVIII веке

• как одна сорокамиллионная часть Парижского меридиана (то есть одна десятимиллионная часть расстояния от северного полюса до экватора по поверхности земного эллипсоида на долготе Парижа).

скорость светауниверсальной мировой константы

Кратные и дольные единицы Править

Основная статья: Приставки СИ

Кратные и дольные единицы

Кратные	Дольные
Величина	Название	Обозначение	Величина	Название	Обозначение
101 Гц	декагерц	даГц	daHz	10−1 Гц	децигерц	дГц	dHz
102 Гц	гектогерц	гГц	hHz	10−2 Гц	сантигерц	сГц	сHz
103 Гц	килогерц	кГц	кHz	10−3 Гц	миллигерц	мГц	mHz
106 Гц	мегагерц	МГц	MHz	10−6 Гц	микрогерц	мкГц	µHz
109 Гц	гигагерц	ГГц	GHz	10−9 Гц	наногерц	нГц	nHz
1012 Гц	терагерц	ТГц	THz	10−10 Гц	пикогерц	пГц	pHz
1015 Гц	петагерц	ПГц	PHz	10−15 Гц	фемтогерц	фГц	fHz
1018 Гц	эксагерц	ЭГц	EHz	10−18 Гц	аттогерц	аГц	aHz
1021 Гц	зеттагерц	ЗГц	ZHz	10−21 Гц	зеттагерц	ЗГц	zHz
1024 Гц	йоттагерц	ИГц	YHz	10−24 Гц	йоктогерц	иГц	yHz
██ — применять не рекомендуется

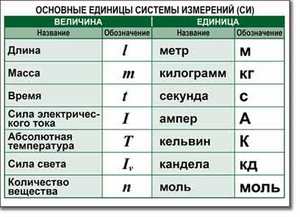
Единицы СИ Править

Названия единиц СИ пишутся со строчной буквы, после обозначений единиц СИ точка не ставится, в отличие от обычных сокращений.

Основные единицы
Величина	Единица измерения	Обозначение
русское название	международн название	русское	между- народное
Длина	метр	metre (meter)	м	m
Масса	килограмм	kilogram	кг	kg
Время	секунда	second	с	s
Сила тока	ampere	А	A
Термодинамическая температура	кельвин	kelvin	К	K
Сила света	кандела	candela	кд	cd
моль	mole	моль	mol

Производные единицы Править

Производные единицы могут быть выражены через основные с помощью математических операций: умножения и деления. Некоторым из производных единиц, для удобства, присвоены собственные названия, такие единицы тоже можно использовать в математических выражениях для образования других производных единиц.

Математическое выражение для производной единицы измерения вытекает из физического закона, с помощью которого эта единица измерения определяется или определения физической величины, для которой она вводится. Например, скорость — это расстояние, которое тело проходит в единицу времени; соответственно, единица измерения скорости — м/с (метр в секунду).

Часто одна и та же единица может быть записана по-разному, с помощью разного набора основных и производных единиц (см., например, последнюю колонку в таблице Производные единицы с собственными названиями). Однако на практике используются установленные (или просто общепринятые) выражения, которые наилучшим образом отражают физический смысл величины. Например, для записи значения момента силы следует использовать Н·м, и не следует использовать м·Н или Дж.

Производные единицы с собственными названиями
Величина	Единица измерения	Обозначение	Выражение
русское название	международное название	русское	международное
радиан	radian	рад	rad	м·м−1 = 1
Телесный угол	стерадиан	steradian	sr	м²·м−2 = 1
Температура по шкале Цельсия¹	градус Цельсия	degree Celsius	°C	°C	K
Частота	герц	hertz	Гц	Hz	с−1
Сила	newton	Н	N	кг·м/c²
Энергия	джоуль	joule	Дж	J	Н·м = кг·м²/c²
Мощность	ватт	watt	Вт	W	Дж/с = кг·м²/c³
Давление	pascal	Па	Pa	Н/м² = кг·м−1·с−2
Световой поток	люмен	lumen	лм	lm	кд·ср
Освещённость	lux	лк	lx	лм/м² = кд·ср·м−2
Электрический заряд	coulomb	Кл	C	А·с
volt	В	V	Дж/Кл = кг·м²·с−3·А−1
Сопротивление	ohm	Ом	Ω	В/А = кг·м²·с−3·А−2
farad	Ф	F	Кл/В = кг−1·м−2·с4·А²
weber	Вб	Wb	кг·м²·с−2·А−1
tesla	Тл	T	Вб/м² = кг·с−2·А−1
henry	Гн	H	кг·м²·с−2·А−2
Электрическая проводимость	siemens	См	S	Ом−1 = кг−1·м−2·с³А²
Радиоактивность	becquerel	Бк	Bq	с−1
gray	Гр	Gy	Дж/кг = м²/c²
sievert	Зв	Sv	Дж/кг = м²/c²
katal	кат	kat	моль·с−1

1. Градус Цельсия — это специальное наименование, используемое вместо наименования «кельвин»

«Единицы СИ»
Основные
Производные

МЕРА ВСЕХ ВЕЩЕЙ

В конце XVIII века, в революционные годы, в Европе существовало более 800 мер длины и веса. Они значительно различались даже в пределах одной Франции: что ни рынок – то и своя мера. Свободная, честная и равноправная торговля была практически невозможна. Торговцы, разъезжавшие по стране, нагло обманывали и обсчитывали народ. Отсутствие официальных обязательных мер мешало и государству, которое даже не знало, каковы подлинные размеры каждой провинции и всей страны.

В 1789 году во Франции началась новая эра, был введён новый революционный календарь. Французы боролись против тирании за идеалы Свободы, Равенства и Братства. Идеологи революции провозгласили: свободный человек – мера всех вещей. Но равенство всех людей предполагает также и единую меру, обязательную для всех.

Законодательное Собрание в Париже постановило, что необходимо определить новую единицу измерения. Созданная для этого специальная Комиссия занялась поисками основы для новой единой меры. Нужно было найти нечто постоянное, неизменное, что не зависит от людского произвола и может служить масштабом. В 1791 году Комиссия, наконец, додумалась до идеи принять за константу окружность земли – земной меридиан. Поскольку меридиан является практически неизменным в достаточно долгий период времени, то за единицу длины решено принять одну десятимиллионную часть четверти земного меридиана. Однако для этого нужно измерить полную окружность Земли по меридиану, а это мудрёная задача.

Французы обладали ценным опытом в измерении расстояний и вычислении площадей. Территорию Франции измерили ещё в XVII веке. Король Людовик XIV приказал осуществить впервые в истории точное измерение территории всей страны. Землемеры выполнили приказ короля с помощью метода триангуляции для топографических съёмок, заключающийся в построении примыкающих друг к другу треугольников. Они провели огромную работу (ищу работу в Тихвине), но результат крайне разочаровал венценосного заказчика – площадь Франции оказалась на 20 процентов меньше, чем считалось. Разочарованный король-Солнце воскликнул: «Ваши труды обошлись мне дорого: я потерял больше земель, чем хотели у меня отнять все мои враги!»

Что представляют собой короткий и полный метр?

В чем разница между короткометражным и полнометражным кино? Какие фильмы снимать легче? Почему известные режиссеры любят короткий метр?

Короткий и полный метр

Мир кино является одним из самых загадочных, особенно для тех, кто находится по эту сторону экрана. Далеко не все знают, как создаются шедевры. Многие стремятся приблизиться к миру кино, посещая курсы актерского мастерства или специализированные фестивали. Если вы планируете стать звездой в этой области, вам нужно знать такие простые понятия, как короткий и полный метр: именно так обозначается продолжительность фильма.

В чем разница?

Длительность первого не превышает 40-50 минут, последний может идти больше двух часов. Но понятие короткого метра не так однозначно: некоторые специалисты называют такими фильмы длительностью до 15 минут, а кино, которое идет в два раза дольше, — средним. Кстати, само название «метр» для обозначения продолжительности фильма связано с длиной пленки, на которой помещается кино.

Короткий метр — это сложно

Исторически сложилось так, что продолжительные фильмы создавались для кинотеатров, то есть для широкого круга лиц. Сегодня короткие картины не менее популярны. Их показывают как перед сеансами в кино, так и на специализированных фестивалях. Ведь, по словам профессионалов, короткий метр снять подчас даже сложнее, чем длинный. Нужно за несколько минут рассказать целую историю и донести до зрителя мораль. Поэтому профессионально снимать такие фильмы решаются далеко не все. А вот начинают свою творческую карьеру с короткого метра большинство: затраты на производство гораздо ниже. Если фильм начинающего режиссера был показан на кинофестивале и высоко оценен критиками — время задумываться о полном метре

Возможно, стоит попробовать себя и в детском кино (как, например, «Озеро героев» или «Осторожно, каникулы«). Но о коротком метре забывать не стоит: это возможность экспериментировать и снимать не только то, что нужно людям, но и то, что хочется самому

Работа над подобным проектом не позволить режиссеру потерять интерес к исследованиям и изучению мира. Да и закончить такую работу при плотном графике можно гораздо быстрее, чем полный метр.

метр I[править]

В Викиданных есть лексема метр (L127288).

Морфологические и синтаксические свойстваправить

падеж	ед. ч.	мн. ч.
Им.	ме́тр	ме́тры
Р.	ме́тра	ме́тров
Д.	ме́тру	ме́трам
В.	ме́тр	ме́тры
Тв.	ме́тром	ме́трами
Пр.	ме́тре	ме́трах

метр

Существительное, неодушевлённое, мужской род, 2-е склонение (тип склонения 1a по классификации А. А. Зализняка).

Корень: -метр-.

Семантические свойстваправить

Значениеправить

1. основная системная единица длины ◆ дом высотой пять метров ◆ метр состоит из ста сантиметров ◆ эталон метра
2. измерительная линейка или лента длиной не менее одного метра (1) ◆ Для вычерчивания крупных чертежей на деревянном полу требуются особые инструменты. <…> 1) складной метр длиной 1—2 м с миллиметровыми делениями… Х. А. Чертков, «Судовой разметчик», 1950 г. ◆ Рабочее место продавца тканей обеспечивается жестким метром и ножницами с округленными концами. Я. А. Каминский, «Организация и техника советской торговли», 1954 г. ◆ Мать в цветастом халате, с метром на шее, с булавкой во рту — так и помрет, видно, в этом наряде. Н. Прокопчик, «Первые страницы», 1990 г. // «Неман»
3. комп. жарг. мегабайт ◆ Отсутствует пример употребления (см. рекомендации).

Гипонимыправить

Родственные словаправить

Ближайшее родство
существительные: метраж, кубометр, нанометр, миллиметр, сантиметр, дециметр, декаметр, гектометр, километр, мегаметр прилагательные: метровый, метрический

Список всех слов с корнем «-метр-»
существительные: дециметр, километр, кресло-километр, комплексонометрия, метр, метроном, микрометр, миллиметр, нанометр, педометр, сантиметр, светометрия, тензометр, тензометрия, трёхкилометровка прилагательные: двухкилометровый, дециметровый, комплексонометрический, метрический, метровый, многокилометровый, многометровый, нанометровый, полуметрический, полуметровый, сантиметровый

Этимологияправить

Происходит от др.-греч.  «измеряю», μέτρον «мера». Русск. метр заимствовано через франц. mètrе, далее через лат. . Использованы данные словаря М. Фасмера. См. Список литературы.

терм

ПРОЕКТ ПОД УГРОЗОЙ СРЫВА

Летом 1792 года, в разгар революционной сумятицы, Французская академия наук поручила двум учёным произвести измерение и вычисление дуги Парижского меридиана, проходящего с севера на юг через всю Францию.

Астрономы Жан-Батист-Жозеф Деламбр и Пьер-Франсуа-Андре Мешен взялись за измерения меридиана между Дюнкерком и Барселоной. Деламбр, впоследствии в 1810 году избранный почётным членом Петербургской академии наук, начал работу в Дюнкерке, на берегу пролива Ла-Манш, а его коллега Мешен отправился со своей экспедицией в Барселону.

Астрономы-картографы покинули Париж 24 июня 1792 года. Деламбр и Мешен шли навстречу друг другу, отмечая точки на своём пути. Где не было высокой колокольни или естественной возвышенности, приходилось строить измерительные башни. Осуществление трудной работы время от времени прерывали бурные политические перемены.

Учёные даже не знали, что в Париже в 1795 году новое центральное правительство восстановило разогнанную радикальными революционерами Академию наук. Чтобы выполнить поставленную задачу, Деламбру и Мешену потребовалось ещё три года работы. Финансовые проблемы, неудобный рельеф местности, депрессия, от которой страдал переутомившийся Мешен, сильно затрудняли завершение измерений.

Но в 1799 году картографы всё же смогли представить в Париже результаты своего труда. Международная комиссия, состоявшая из учёных одиннадцати стран, проверяла итоги работы французских астрономов. Члены комиссии пришли к заключению, что вычисления верны. Парижское Национальное собрание 10 декабря 1799 года провозгласило введение новой единственной метрической системы. В тот год появился на свет архивный метр – первый в истории эталон метра. Отлитый из платины метр был передан на хранение в Национальный архив Франции.

Погонный метр, это сколько?

Какие же товары измеряют погонными метрами? Погонный метр, это единица измерения длины таких товаров:

• для которых при продаже значения ширины, высоты или диаметра сечения не имеют значения;
• которые при использовании, требуют стыковки между собой его фрагментов;
• предназначенных для ограждений, например, металлических заборов или заборов из другого материала.

Такие товары в магазинах бывают в виде рулонов, бобин, плит и т. п. Например:

1. в виде рулонов бывают:

   • ковровые покрытия,
   • асбестовое полотно,
   • линолеум,
   • ткани,
   • искусственные газонные покрытия,
   • полиэтиленовая пленка
   • и др.;

2. в виде бобин бывают:

   • кабели,
   • провода,
   • нитки,
   • и др.;

3. в виде плит/отрезов бывают:

   • облицовочные камни,
   • ламинат,
   • фанера,
   • материал для мебели,
   • и др.

4. в виде длинных «палок «бывают:

   • плинтусы,
   • карнизы,
   • доски для настила пола,
   • рейки,
   • и др.

Чтобы при покупке необходимого вам товара, измеряемого в п. м, не ошибиться в правильности определения количества этого товара, надо обязательно точно знать параметры помещения, изделия, материала, для которого вы приобретаете этот товар.

Как же правильно рассчитать количество товара? Ниже приведены примеры расчетов.

Расчет при покупке коврового покрытия

Допустим, вы хотите купить ковровое покрытие для комнаты площадью 20 м2 (длиной 5 м и шириной 4 м)

Вам важно, чтобы по длине комната была покрыта полностью, что касается ширины, то допустимо, что по краям комнаты могут быть места не застеленные. Вы приходите в магазин и перед вами большой выбор ковровых покрытий, как вам правильно сориентироваться в ситуации?

Особенностью выбора коврового покрытия, является то, что оно должно быть цельным куском, без стыковки, поэтому критерием выбора должна быть его ширина.

Таким образом, вы должны купить 5 м того покрытия, ширина которого вас больше устроит.

Расчет для покупки линолеума

Вы идете покупать линолеум для кухни шириной 2,5 м и длиной 5 м. В магазине вы можете увидеть рулоны разной ширины: 1,5 м, 2,0 м и 2,5 м. Сколько линолеума вы должны купить? Вы должны выбрать линолеум шириной 2,5 метра (т. е. по ширине кухни) и купить его 5 п. м. и одним куском застелить кухонный пол. Но это тот идеальный случай, когда ширина линолеума совпадает с шириной кухни.

А, что делать, если кухня шириной 3 метра? В этом случае одним куском пол не застелешь. Надо думать, как состыковать два куска. Значит, для этого надо взять 10 п. м. от рулона шириной 1,5 м (или просите продавца отрезать два куска по 5 п. м., чтобы потом не резать самому). В этом случае стык будет проходить ровно посередине кухни. Линолеум можно класть не только в его длину, но и по ширине, таким образом, варьировать место шва и количество линолеума в зависимости от площади покрываемой поверхности.

Расчет для покупки тканей

Что касается тканей, то тут тоже есть свои нюансы, связанные с погонным метражом.

Допустим, вам надо купить тюль для занавеси на окно, спаренное с дверью, выходящей на балкон. Расчет будет такой: ширина рулона – это будет длина вашей занавеси, а для ширине занавеси мы должны взять двойную ширину окна (с учетом на фалды). Таким образом, при ширине окна с дверью в 3 м, вам надо купить 6 п. м. занавеси.

Расчет для покупки полиэтиленовой пленки для оборудования теплицы

Для того, чтобы купить полиэтиленовую пленку для оборудования теплицы, надо нарисовать на бумаге в правильном масштабе каждый фрагмент теплицы, который должен быть обтянут пленкой. Затем посчитать все их параметры: длины и ширины, сложить и рассчитать необходимое количество пленки. Не забывайте дополнительное количество на закрепление пленки к фрагментам теплицы

При покупке полиэтиленовой пленки надо обращать внимание на то, что пленка в рулоне, как правило, бывает двойная, значит, при покупке необходимая цифра должна быть поделена на 2

Расчет для покупки плинтусов и карнизов

Для покупки плинтусов или карнизов, надо сделать замер периметра пола и потолка с учетом на выступы балок, ниш и т. д. Суммировав все размеры можно определить сколько п. м. плинтусов или карнизов вам надо.

Расчет для покупки электропровода или кабеля

Допустим, вам надо посчитать сколько п. м. провода вам понадобится для прокладки электропроводки в дачном коттедже. Тут существует два способа:

• по готовой электрической схеме;
• по площади коттеджа.

Первый вариант более грамотный, так как в этом случае вы будете точно знать кабель какого сечения, к каким точкам и для каких целей будет подведен. Исходя из этого, можно точно подсчитать, сколько п. м. какого кабеля и, с каким сечением вам будет нужно. При этом надо помнить о запасе на монтаж. Обычно, к суммарному количеству требуемых п. м, надо прибавить не менее 2 м.

Второй вариант очень прост: надо определить общую площадь дома и умножить ее на два и прибавить на запас 2 м.

Сколько в N км метров?

Давайте попробуем узнать сколько метров в километре в приведенных выше применах. Итак начнем.

Задача #1: В 1 километре сколько метров? Решение: Используя, приведенную выше формулу, получаем: 1 * 1000 = 1 000 метров. Ответ: в 1 километре 1000 метров.	Задача #6: В 8 км сколько м? Решение: 8 * 1 000 = 8 000 метров. Ответ: в 8 километрах 8 000 метров.
Задача #2: 2 километра – это сколько метров? Решение: Используя, приведенную выше формулу, получаем: 2 * 1 000 = 2 000 метров. Ответ: в 2 километрах 2000 метров.	Задача #7: В 20 км сколько метров? Решение: 20 * 1 000 = 20 000 метров. Ответ: в 20 км 20 000 метров.
Задача #3: В 3 км сколько метров? Решение: 3 * 1 000 = 3 000 метров. Ответ: в 3 км 3 000 метров.	Задача #8: В 30 км сколько метров? Решение: 30 * 1 000 = 30 000 метров = 30 тыс. м. Ответ: в 30 км 30 тыс. метров.
Задача #4: В 5 километрах сколько метров? Решение: 5 * 1 000 = 5 000 метров. Ответ: в 5 км 5 000 метров.	Задача #9: Сколько в 15 км м? Решение: 15 * 1 000 = 15 000 метров = 15 тыс. м. Ответ: в 15 км — 15 тысяч метров.
Задача #5: В 4 км сколько метров? Решение: 4 * 1000 = 4 000 метров. Ответ: в 4 километрах 4 000 метров.	Задача #10: Сколько м в 9 км? Решение: 9 * 1000 = 9 000 метров Ответ: в 9 километрах 9 000 метров.

Определение — метр

Определение метра с помощью штрихового эталона неудовлетворительно в двух отношениях. Во-первых, штриховой эталон метра является искусственным и в случае утраты не может быть воспроизведен.
 

Определение метра, действующее с 1889 г., основанное на международном платино-иридиевом эталоне, отменяется.
 

Определение метра, положенное в основу Международной системы ( СИ), приняла XI Генеральная конференция по мерам и весам в 1960 г.: Метр — длина, равная 1650763 73 длины волны в вакууме излучения, соответствующего переходу между уровнями 2р10 и 5d5 атома Кгвб.
 

Архивный метр. — гоперсчное сечение. 6 — вид сверху.

Определение метра с помощью штрихового эталона неудовлетворительно в двух отношениях.
 

Определение метра, действующее с 1889 г., основанное на международном пл.
 

Это определение метра было принято на XVII Генеральной конференции мер и весов в декабре 1985 г. после утверждения единых эталонов времени, частоты и длины.
 

При таком определении метра, принятом XVII Генеральной конференцией по мерам и весам в 1983 г., длина не может считаться основной физической величиной, так как выражается через скорость и время. По всей вероятности за этим решением XVII Генеральной конференции по мерам и весам должно последовать изменение структуры Международной системы единиц.
 

Консультативного комитета по определению метра с 5 довлетворением отметила, что воспроизведение единицы длины с помощью длины волны спектральной линии, определяемой переходом между уровнями энергии 2рю и 5ds атома Кг86 имеет еще очень большой запас точности и вполне удовлетворяет запросам современной физики и техники.
 

Измерения длины волны принципиально важны в связи с определением метра через длину световой волны и для ряда тонких спектроскопических исследований.
 

За нормальную температуру обыкновенно принимают 20, однако для определения метра, ома, нормального барометрического давления 760 мм рт. ст., физической атм.
 

Все же ученые периодически повторяли попытки найти природный базис для определения метра, так как иначе невозможно восстановить его точную длину в случае утраты существующих эталонов или медленного изменения их длины. Такой базис был найден — длина световой волны. Он постоянен и открывает перспективу повышения точности линейных измерений. В результате исследований, проведенных в ряде стран, длина метра была определена в 1650763 73 длины волны оранжевой линии крипто-на-86; погрешность воспроизведения составляет 0 05 мкм. Так обретен, и теперь навечно, естественный и неразрушимый эталон длины.
 

Это значение оранжевой линии Кг86 в вакууме и было принято для определения метра. При сравнении длин волн источником света с естественным Cd служила лампа Майкельсона при полном соблюдении условий спецификации VII Генеральной конференции. Источником света с Кг86 во всех лабораториях служила лампа, рекомендованная Физико-техническим институтом ( ФРГ), описание которой приведено выше. Средние квад-ратические погрешности до некоторой степени характеризуют высокую точность воспроизведения длины волны.
 

В период между XI Генеральной конференцией и III сессией Консультативного комитета по определению метра в Международном бюро мер и весов и в национальных лабораториях были повторены работы по изучению контура оранжевой линии Кг86 и изучены смещения длин волн в зависимости от направления наблюдения свечения в капиллярах лампы.
 

В 1983 г. на XVII Генеральной конференции по мерам и весам было принято определение метра, согласно которому метр представляет собой расстояние, проходимое в вакууме плоской электромагнитной волной за 1 / 299792458 долю секунды. Метр приближенно равен 1 / 40000000 доле длины земного меридиана.
 

Примечания

Комментарии

1. metro cattolico (lit. «catholic мера»), заимствовано из греческого μέτρον καθολικόν (métron katholikón)
2. Идея секундного маятника для назначения стандартной длины тем не менее окончательно не умерла, и такой стандарт был использован для определения длины ярда в Великобритании в период 1843—1878 годов.

Источники

1. ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 77—82. — 240 с. — ISBN 5-7050-0118-5.
2. ↑
3. ↑  (недоступная ссылка). Федеральный информационный фонд по обеспечению единства измерений. Росстандарт. Дата обращения 28 февраля 2018.
4.  (недоступная ссылка). BIPM. Дата обращения 22 июня 2019.
5.  (недоступная ссылка). Федеральный информационный фонд по обеспечению единства измерений. Росстандарт. Дата обращения 28 февраля 2018.
6. Окунь Л. Б. // Физическая энциклопедия : / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 552—556. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
7. Wilkins, John (1668), , London: Gillibrand, http://www.metricationmatters.com/docs/WilkinsTranslationLong.pdf>.
8. Misura Universale, 1675.
9. Poynting, John Henry & Thompson, Joseph John (1907), (4th ed.), London: Charles Griffin, с. 20, https://books.google.com/books?id=TL4KAAAAIAAJ&pg=PA20>.
10. ↑ Grand dictionnaire universel du XIXe siècle, Paris: Pierre Larousse, 1866—1877, p. 163—164.
11. , MacTutor, http://www-history.mcs.st-andrews.ac.uk/Biographies/Borda.html>. Проверено 13 августа 2010..
12.  (англ.). International Bureau of Weights and Measures. Дата обращения 12 июля 2010.
13. Гевара И., Карлес П. Измерение мира. Календари, меры длины и математика.. — М.: Де Агостини, 2014. — С. 125—126. — 160 с. — (Мир математики: в 45 томах, том 38). — ISBN 978-5-9774-0733-5.
14.  (недоступная ссылка). История измерений. Дата обращения 12 июля 2010.
15. — статья из энциклопедии «Кругосвет»
16. Ландсберг Г. С. Оптика. — М.: Физматлит, 2003. — С. 387. — ISBN 5-9221-0314-8.
17. Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 78. — 240 с. — ISBN 5-7050-0118-5.

Ритм и метр

Метр — понятие абстрактное. В музыкальном произведении метр может быть никак не выражен динамически (звуками) или графически (нотами), а лишь существовать в воображении исполнителя и слушателя. Так, важнейшая категория метра доля (принято различать сильную и слабую доли), особенно в классической тактовой метрике, полагается как психологический, а не материальный объект. Ритм, в отличие от метра, конкретен — он выражается отношением длительностей «реальных» звуков и как правило выписан в нотах.

Ритм как организация музыки во времени присутствует всегда («в начале был ритм», по знаменитому выражению Г. фон Бюлова). Метр может быть, а может и отсутствовать. Например, ритм есть в григорианском хорале и в древнерусском знаменном распеве, но метра в них нет. Метр (как правило организации ритма) находят в любых танцевальных жанрах (например, в сицилиане и вальсе) и шире — в любой профессиональной музыке классико-романтического периода.

Практическая реализация (интерпретация) метра, как и ритма, достаточно условна. При том, что исполнитель может допускать агогические отклонения (особенно в романтической музыке XIX — начала XX веков, например, в музыке Шопена и Скрябина), метрическая сетка всё же психофизиологически ощущается как неизменный остов (правило) ритмической структуры.

[править] Источники

1. «Misura Universale», 1675.
2. Poynting, John Henry & Thompson, Joseph John (1907), «A Textbook of Physics: Properties of Matter» (4th ed.), London: Charles Griffin, с. 20, <http://books.google.com/books?id=TL4KAAAAIAAJ&pg=PA20>.

Основные единицы	Ампер · Кандела · Кельвин · Килограмм · Метр · Моль · Секунда
Производные единицы	Беккерель · Ватт · Вебер · Вольт · Генри · Герц · Градус Цельсия · Грей · Джоуль · Зиверт · Катал · Кулон · Люкс · Люмен · Ньютон · Ньютон-метр · Ом · Паскаль · Радиан · Сименс · Стерадиан · Тесла · Фарад
Принятые для использования с СИ	Ангстрем · Астрономическая единица · Гектар · Градус дуги (Минута дуги, Секунда дуги) · Дальтон (Атомная единица массы) · Децибел · Литр, Кубический километр · Микрограмм (Миллиграмм) · Микросекунда (Миллисекунда, Наносекунда) · Микрометр (Нанометр, Сантиметр, Фемтометр, Километр) · Непер · Сутки (Час, Минута) · Тонна · ЭлектронвольтАтомная система единиц · Естественная система единиц
См. также	История метрической системы · Квантовая система единиц · Новые определения СИ · Планковская длина · Преобразование единиц · Приставки СИ · Система физических величин

ТРИАНГУЛЯЦИЯ

Начиная с XVII века в картографии применялась триангуляция. В первую очередь на равнинной местности нужно проложить прямую линию с помощью деревянных реек определённой длины или цепей, натянутых на колышки. Кроме того, необходимо обозначить хорошо просматривающуюся триангуляционную точку, например, заметный издалека холмик или шпиль на церковной колокольне. Из точек, где заканчивается первая прямая линия, намечаются линии к этой третьей точке и измеряются углы. Поскольку известна длина одной стороны треугольника, а также два угла, можно по тригонометрическим формулам вычислить две другие стороны треугольника и его площадь. Из каждой вершины полученного треугольника на местности можно наметить с помощью колышков и реек следующие треугольники. Таким образом, в результате сложения площадей треугольников на местности можно определить площадь больших участков. В некоторых случаях картографы устанавливали специальные измерительные башенки для удобства обозначения точек на местности.

Неоценимую помощь в многотрудной работе оказали землемерам так называемые неподвижные звёзды, которые издавна использовались в качестве ориентиров при навигации. Самый яркий пример – Полярная звезда. Чем севернее находится точка наблюдения, тем выше стоит на небосклоне Полярная звезда. Если в северной точке отрезка наблюдения картографы обнаруживали Полярную звезду на десять градусов выше, чем на южном конце отрезка, они знали, что они измерили на Земле дугу меридиана, соответствующую десяти градусам. Этот отрезок умножается на девять и получается длина дуги, составляющей четверть окружности с центральным углом 90 градусов.

Метр и размер

Метр и тактовый размер — близкие понятия, которые некоторыми воспринимаются почти как синонимы. Однако есть различие — размер, в отличие от метра, задает относительную длительность каждой доли. Например, размер «3/4» говорит о том, что в такте будет 3 доли, каждая из которых представлена (нотирована) четвертной нотой. Можно сказать, что размер — «числовое» представление метра с указанием длительности каждой доли, использующееся в нотных обозначениях.

Простые метры

Простые метры — это двудольные или трёхдольные метры, имеющие одну сильную долю (акцент): «1 из 2» или «1 из 3».

Двухдольный метр — метр, в котором сильные доли повторяются равномерно через одну долю (состоит из одной сильной доли и одной слабой). Эти метры выражают такие размеры, как «2/2», «2/4» и «2/8».

Трёхдольный метр — метр, в котором сильные доли повторяются равномерно через 2 доли (состоит из одной сильной доли и двух слабых). Эти метры выражают такие размеры, как «3/2», «3/4», «3/8», реже встречается «3/16».

Сложные метры

Сложные (составные) метры — метры, полученные при слиянии двух и более простых метров (например, 5/4, получаемый из комбинации 3/4 + 2/4, или наоборот). Благодаря этому сложный метр может иметь несколько сильных долей, количество которых соответствует количеству простых метров, входящих в его состав.

Акцент первой доли сложного метра сильнее остальных его акцентов, поэтому эта доля называется сильной. А доли с более слабыми акцентами называются относительно сильными долями.

Наиболее часто используемые сложные размеры для выражения сложных метров:

• четырёхдольные («4/4», «4/2» и редко «4/8»);
• шестидольные («6/4», «6/8» и редко «6/16»);
• девятидольные («9/8» и редко «9/4» и «9/16»);
• двенадцатидольные («12/8» и редко «12/16»).

Единицы СИ (система единиц)[править]

Названия единиц СИ (система единиц) пишутся со строчной буквы, после обозначений единиц СИ точка не ставится, в отличие от обычных сокращений.

Основные единицы
Величина	Единица измерения	Обозначение
русское название	международн. название	русское	между- народное
Длина	метр	metre (meter)	м	m
Масса	килограмм	kilogram	кг	kg
Время	секунда	second	с	s
Сила тока	ампер	ampere	А	A
Термодинамическая температура	кельвин	kelvin	К	K
Сила света	кандела	candela	кд	cd
Количество вещества	моль	mole	моль	mol

Производные единицыправить

Производные единицы могут быть выражены через основные с помощью математических операций: умножения и деления. Некоторым из производных единиц, для удобства, присвоены собственные названия, такие единицы тоже можно использовать в математических выражениях для образования других производных единиц.

Математическое выражение для производной единицы измерения вытекает из физического закона, с помощью которого эта единица измерения определяется или определения физической величины, для которой она вводится. Например, скорость — это расстояние, которое тело проходит в единицу времени; соответственно, единица измерения скорости — м/с (метр в секунду).

Часто одна и та же единица может быть записана по-разному, с помощью разного набора основных и производных единиц (см., например, последнюю колонку в таблице Производные единицы с собственными названиями). Однако на практике используются установленные (или просто общепринятые) выражения, которые наилучшим образом отражают физический смысл величины. Например, для записи значения момента силы следует использовать Н·м, и не следует использовать м·Н или Дж.

Производные единицы с собственными названиями
Величина	Единица измерения	Обозначение	Выражение
русское название	международное название	русское	международное
Плоский угол	радиан	radian	рад	rad	м·м−1 = 1
Телесный угол	стерадиан	steradian	ср	sr	м²·м−2 = 1
Температура по шкале Цельсия¹	градус Цельсия	degree Celsius	°C	°C	K
Частота	герц	hertz	Гц	Hz	с−1
Сила	ньютон	newton	Н	N	кг·м/c²
Энергия	джоуль	joule	Дж	J	Н·м = кг·м²/c²
Мощность	ватт	watt	Вт	W	Дж/с = кг·м²/c³
Давление	паскаль	pascal	Па	Pa	Н/м² = кг·м−1·с−2
Световой поток	люмен	lumen	лм	lm	кд·ср
Освещённость	люкс	lux	лк	lx	лм/м² = кд·ср·м−2
Электрический заряд	кулон	coulomb	Кл	C	А·с
Разность потенциалов	вольт	volt	В	V	Дж/Кл = кг·м²·с−3·А−1
Сопротивление	ом	ohm	Ом	Ω	В/А = кг·м²·с−3·А−2
Электроёмкость	фарад	farad	Ф	F	Кл/В = кг−1·м−2·с4·А²
Магнитный поток	вебер	weber	Вб	Wb	кг·м²·с−2·А−1
Магнитная индукция	тесла	tesla	Тл	T	Вб/м² = кг·с−2·А−1
Индуктивность	генри	henry	Гн	H	кг·м²·с−2·А−2
Электрическая проводимость	сименс	siemens	См	S	Ом−1 = кг−1·м−2·с³А²
Радиоактивность	беккерель	becquerel	Бк	Bq	с−1
Поглощённая доза ионизирующего излучения	грэй	gray	Гр	Gy	Дж/кг = м²/c²
Эффективная доза ионизирующего излучения	зиверт	sievert	Зв	Sv	Дж/кг = м²/c²
Активность катализатора	катал	katal	кат	kat	моль·с−1

1. Градус Цельсия — это специальное наименование, используемое вместо наименования «кельвин»

Примечания

Комментарии

1. metro cattolico (lit. «catholic мера»), заимствовано из греческого μέτρον καθολικόν (métron katholikón)
2. Идея секундного маятника для назначения стандартной длины тем не менее окончательно не умерла, и такой стандарт был использован для определения длины ярда в Великобритании в период 1843—1878 годов.

Источники

1. ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 77—82. — 240 с. — ISBN 5-7050-0118-5.
2. ↑
3. ↑  (недоступная ссылка). Федеральный информационный фонд по обеспечению единства измерений. Росстандарт. Дата обращения 28 февраля 2018.
4.  (недоступная ссылка). BIPM. Дата обращения 22 июня 2019.
5.  (недоступная ссылка). Федеральный информационный фонд по обеспечению единства измерений. Росстандарт. Дата обращения 28 февраля 2018.
6. Окунь Л. Б. // Физическая энциклопедия : / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 552—556. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
7. Wilkins, John (1668), , London: Gillibrand.
8. Misura Universale, 1675.
9. Poynting, John Henry & Thompson, Joseph John (1907), (4th ed.), London: Charles Griffin, с. 20.
10. ↑ Grand dictionnaire universel du XIXe siècle, Paris: Pierre Larousse, 1866—1877, p. 163—164.
11. , MacTutor. Проверено 13 августа 2010..
12.  (англ.). International Bureau of Weights and Measures. Дата обращения 12 июля 2010.
13. Гевара И., Карлес П. Измерение мира. Календари, меры длины и математика.. — М.: Де Агостини, 2014. — С. 125—126. — 160 с. — (Мир математики: в 45 томах, том 38). — ISBN 978-5-9774-0733-5.
14.  (недоступная ссылка). История измерений. Дата обращения 12 июля 2010.
15. — статья из энциклопедии «Кругосвет»
16. Ландсберг Г. С. Оптика. — М.: Физматлит, 2003. — С. 387. — ISBN 5-9221-0314-8.
17. Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 78. — 240 с. — ISBN 5-7050-0118-5.