Куб

Другие виды бумажных поделок

Из получившихся кубиков можно выполнять различные объёмные поделки:

1. Гирлянда. Её можно собрать из большого количества цветных кубиков. Эти кубики можно собрать как по шаблону, так и в стиле оригами. Главное — проколоть их и надеть на верёвочку, и тогда у вас получится очень красивая гирлянда.
2. Игральная кость выполняется очень просто. Необходимо сделать маленький куб по одному из предложенных способов. А потом нужно нарисовать точки на каждой из сторон вашего куба.
3. Робот также делается очень легко. Необходимо сделать 2 кубика — большой и маленький. Большой кубик будет служить головой робота, а маленький — туловищем. А также необходимо сделать 4 объёмных прямоугольника. Они нужны нам для того, чтобы сделать нашему роботу руки и ноги. Чтобы ваш робот двигался, соедините все его детали с помощью зубочистки.

Наверняка очень мало людей знает, что можно сделать бумажный кубик Рубика своими руками. Для этого вам понадобятся следующие предметы:

1. Цветная бумага.
2. Линейка.
3. Карандаш.
4. Ножницы.
5. Прозрачный скотч.

Этапы выполнения кубика Рубика:

1. Возьмите 6 листов цветной бумаги с разными цветами.
2. Из каждого листа вырежьте по 8 квадратиков размером 4*4.
3. На каждом квадратике необходимо провести центральную линию, и сложить его края к центру.
4. На получившейся заготовке также проведите центральную линию, и согните края заготовки к этой линии.
5. Необходимо собрать первый кубик. Составьте цвета в том порядку, который вам нравится.
6. Соберите кубик из шести заготовок разного цвета.
7. Повторите этой действие для оставшихся заготовок.
8. Составьте 8 получившихся кубиков в 4 пары.
9. Цвет, который находится у первых двух пар вверху, у следующих двух пар должен быть внизу.
10. Склейте каждую пару так, чтобы кубики могли двигаться.
11. Возьмите две пары и переверните их набок. Склейте две верхние грани кубиков.
12. Сделайте то же самое с обратной стороны склейки.
13. С оставшимися двумя парами сделайте то же самое.
14. У вас получились две основные части вашего изделия. Теперь их надо соединить.
15. Для этого положите их в такой же последовательности, как они лежали до склеивания.
16. Две центральные пары необходимо склеить.
17. Далее, сложите их в куб, и склейте те стороны, которые видите прямо перед собой.

У вас получился куб-трансформер. Его можно собирать как кубик Рубика, а также он может превращаться в прямоугольник.

Теперь вы знаете, как можно сделать куб из бумаги своими руками и без проблем сможете сделать его самостоятельно. Ваш ребёнок будет доволен, ведь все полки в его игровой комнате будут заставлены различными поделками. Успехов вам!

Проекция на плоскость

Формирование гиперкуба может быть
представлено следующим способом:

• Две точки A и B могут быть соединены,
  образуя отрезок AB.
• Два параллельных отрезка AB и CD могут
  быть соединены, образуя квадрат ABCD.
• Два параллельных квадрата ABCD и EFGH могут
  быть соединены, образуя куб ABCDEFGH.
• Два параллельных куба ABCDEFGH и IJKLMNOP могут
  быть соединены, образуя гиперкуб
  ABCDEFGHIJKLMNOP.

Последнюю структуру нелегко представить,
но возможно изобразить ее проекцию на
двухмерное или трехмерное пространство.
Более того, проекции на двухмерную
плоскость могут быть более полезны
возможностью перестановки позиций
спроецированных вершин. В этом случае можно
получить изображения, которые больше не
отражают пространственные отношения
элементов внутри тессеракта, но
иллюстрируют структуру соединений вершин,
как на примерах ниже.

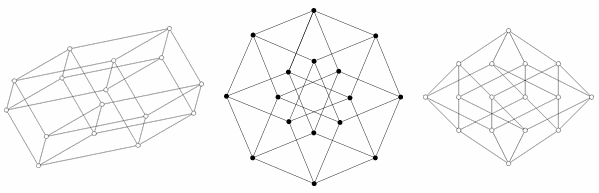
На первой иллюстрации показано, как в
принципе образуется тессеракт путем
соединения двух кубов. Эта схема похожа на
схему создания куба из двух квадратов. На
второй схеме показано, что все ребра
тессеракта имеют одинаковую длину. Эта
схема также заставляют искать соединенные
друг с другом кубы. На третьей схеме вершины
тессеракта расположены в соответствии с
расстояниями вдоль граней относительно
нижней точки. Эта схема интересна тем, что
она используется как базовая схема для
сетевой топологии соединения процессоров
при организации параллельных вычислений:
расстояние между любыми двумя узлами не
превышает 4 длин ребер, и существует много
различных путей для уравновешивания
нагрузки.

Отсечение задних граней

OpenGL рассчитан на дополнительное отсечение невидимых поверхностей, построенное по принципу отсечения задних граней. По умолчанию включён режим, аналогичный вызову , и OpenGL делит примитивы на две группы:

• те, вершины которых перечисляются против часовой стрелки (GL_CCW), становятся передними гранями (GL_FRONT)
• те, вершины которых перечисляются по часовой стрелке (GL_CW), становятся задним гранями (GL_BACK)

Вызов изменит классификацию на обратную: перечисление по часовой даст переднюю грань, перечисление против часовой даст заднюю.

Независимо от того, в каком порядке были заданы исходные вершины, если после всех преобразований грань объёмного тела повёрнута к нам лицевой стороной — порядок обхода сохранится, а если её перекроют другие грани — порядок обхода сменится на противоположный.

Режим отсечения граней можно включить командой , после чего можно выбрать способ отсечения: убирать задние грани (GL_BACK), передние грани (GL_FRONT) или оба вида граней (GL_FRONT_AND_BACK).

Соберём всю инициализацию состояния OpenGL в метод OnWindowInit, который будет вызываться один раз поле инициализации окна

Чтобы метод был вызван своевременно, его можно объявить виртуальным в классе CAbstractWindow и вызывать в методе Show:

Геометрические особенности трехмерной проекции четырехмерного гиперкуба (3ПГК-4)

Давайте рассмотрим геометрические особенности трехмерной проекции четырехмерного гиперкуба (3ПГК-4),
построенного с помощью трехмерной проекции системы осей координат для четырехмерного измерения.

На рис. 2.6 представлен чертеж 3ПГК-4, начерченный только по вершинам 3ПГК-4, без
осей координат и вспомогательных линий; для удобства масштаб чертежа уменьшен в два раза.

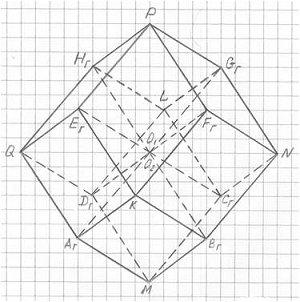
Рис. 2.6

Обратите внимание: через вершины трехмерной проекции четырехмерного гиперкуба (3ПГК-4)
вписывается куб AгBгCгDгEгFгGгHг. Это очень важный факт для осмысления 3ПГК-4

Рисунок 2.7 дает очень наглядное представление о
расположении вершин, ребер, граней 3ПГК-4. Смотрите: восемь внутренних ребер 3ПГК-4
(AгO, BгO, CгO, DгO, EгO,
FгO, GгO и HгO)
расположены на больших диагоналях вписанного в 3ПГК-4 куба, а четыре ребра 3ПГК-4
(EгP, FгP, GгP и HгP) образуют четырехугольную
пирамиду PEгFгGгHг с основанием в виде квадрата
EгFгGгHг, который является одной из шести граней
вписанного в 3ПГК-4 куба

Причем, что очень важно, ребра этой пирамиды параллельны
большим диагоналям вписанного в 3ПГК-4 куба, то есть
PEг || GгAг, PFг || HгBг,
PGг || EгCг и PHг || FгDг ,
при этом PEг = GгO, PFг = HгO,
PGг = EгO и
PHг = FгO (разумеется, что в точке О совмещены две вершины О1 и О2). А из этого следует, что пирамида PEгFгGгHг
геометрически равна пирамиде OEгFгGгHг.

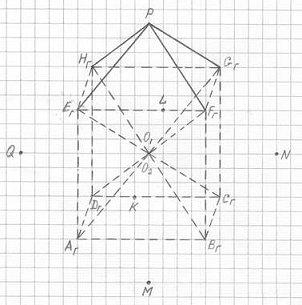
Рис. 2.7

Вершина Р является общей для шести граней-ромбов, равных между собой,
причем четыре ромба (PE_гKF_г , PF_гNG_г,
PG_гLH_г и PH_гQE_г) являются внешними
гранями 3ПГК-4, а два ромба (PE_гOG_г и PF_гOH_г)
являются внутренними гранями.

В рисунке 1.1 показано, что 3ПГК-4 пересекают пять параллельных между собой плоскостей,
равноотстоящих друг от друга. Так вот, по рисункам 2.6 и 2.7 расположение этих пяти
плоскостей определится следующим образом: вторая плоскость (Р_II)
проходит через вершины E_г, F_г, G_г и H_г;
четвертая плоскость (Р_IV) проходит через вершины
A_г, B_г, C_г и D_г; третья плоскость (Р_III)
проходит через вершины Q, K, O₁, O₂, N и L;
а первая (P_I) и пятая (Р_V) плоскости проходят через вершины
P и M соответственно.

Итак, на примере только одной пирамиды PE_гF_гG_гH_г
определены некоторые очень важные свойства трехмерной проекции четырехмерного гиперкуба (3ПГК-4).
Но если учесть, что остальные пять пирамид, построенные на других пяти гранях вписанного куба,
геометрически равны
пирамиде PE_гF_гG_гH_г, то, осмыслив безупречную
симметрию и гармонию 3ПГК-4, можно только изумляться совершенству
трехмерной проекции четырехмерного гиперкуба.

Совершенство трехмерной проекции четырехмерного гиперкуба (3ПГК-4) подтверждается и тем,
что через вершины 3ПГК-4 можно построить не только вписанный куб
A_гB_гC_гD_гE_гF_гG_гH_г,
но и описанный куб A’B’C’D’E’F’G’H’ – через вершины P, Q, K, N, L и M (см. рис. 2.8).
А через вершины нашего вписанного куба, как известно математикам, легко вписывается еще одно
«тело Платона» — тетраэдр. Кроме того, через шесть вершин 3ПГК-4 (P, Q, K, N, L и M)
вписывается и еще одно «тело Платона» — октаэдр (см. рис. 2.9). Ребрами этого октаэдра
являются 12 больших диагоналей ромбов – всех 12-ти внешних граней 3ПГК-4. А так как поверхность
трехмерной проекции четырехмерного гиперкуба состоит из 12-ти ромбов, то эта геометрическая
фигура называется еще ромбододекаэдром (см. рис. 2.8).

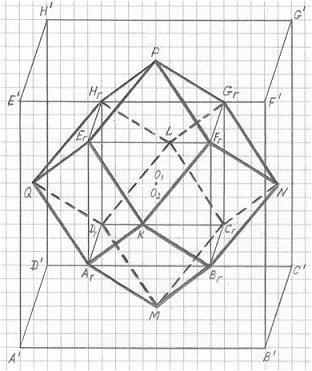
Рис. 2.8

Рис. 2.9

Предлагаю вашему вниманию рисунки 2.10, 2.11, 2.12 и 2.13. Это одна и та же
геометрическая фигура – трехмерная проекция четырехмерного гиперкуба (3ПГК-4).
В этих чертежах нет искажений, я старалась выполнить их точно. Вершины, обведенные
кружками, — это совмещенные вершины. Вот как легко можно начертить 3ПГК-4 (рис. 2.12, рис. 2.13).

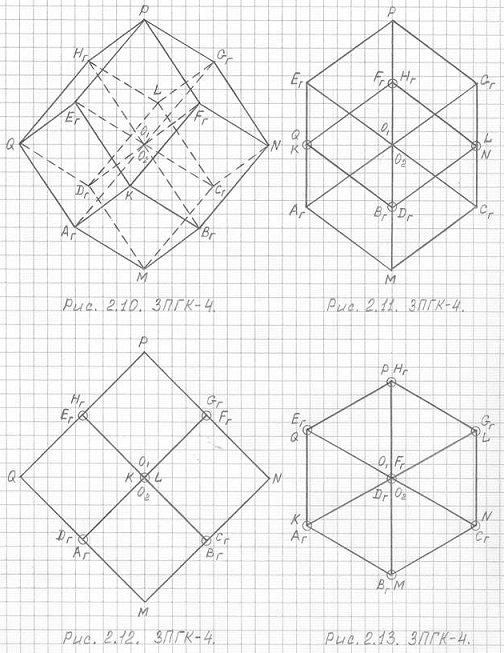
Рис. 2.10 — Рис. 2.13

Трехмерная проекция четырехмерного гиперкуба имеет 13 осей симметрии: семь осей симметрии проходят
через 14 противоположных вершин, расположенных на поверхности 3ПГК-4
(PM, QN, LK, E_гC_г, F_гD_г, G_гA_г и H_гB_г),
и шесть осей симметрии проходят через центры двенадцати противолежащих ромбов (граней), образующих поверхность 3ПГК-4.

Трехмерная проекция четырехмерного гиперкуба имеет 9 плоскостей симметрии:
PG_гC_гMA_гE_г, PF_гB_гMD_гH_г,
NC_гD_гQE_гF_г, NB_гA_гQH_гG_г,
KA_гD_гLG_гF_г, KE_гH_гLC_гB_г,
PNMQ, PKML и KNLQ.

Трехмерная проекция четырехмерного гиперкуба имеет три сферы с центром О₁О₂:
большая сфера описывает вершины P, N, K, Q, L и M, средняя сфера описывает вершины
A_г, B_г, C_г, D_г, E_г, F_г, G_г и H_г,
а меньшая сфера вписывается через центры всех двенадцати граней (ромбов), образующих поверхность 3ПГК-4.

Развёртки

Итак, житель четырёхмерного пространства может увидеть
трёхмерный объект одновременно со всех сторон.
Можем ли мы одновременно со всех сторон увидеть трёхмерный
куб? Глазом — нет. Но люди придумали способ, как
изобразить на плоском рисунке все грани трёхмерного куба одновременно.
Такое изображение называется развёрткой.

Развёртка трёхмерного куба

Как образуется развёртка трёхмерного куба все наверно знают.
Этот процесс показан на анимации.

Для наглядности края граней куба сделаны полупрозрачными.

Следует отметить, что мы способны воспринять эту двумерную картинку
только благодаря воображению. Если рассмотреть фазы разворачивания
с чисто двумерной точки зрения, то процесс будет казаться странным
и совсем не наглядным.

Он выглядит, как постепенное появление сперва очертаний
искажённых квадратов, а потом их расползание на свои места
с одновременным принятием необходимой формы.

Если смотреть на разворачивающийся куб в направлении
одной из его граней (с этой точки зрения куб выглядит как
квадрат), то процесс образования развёртки ещё менее нагляден.
Всё выглядит как выползание квадратов из начального квадрата
(не развёрнутого куба).

Но не наглядна развёртка только для глаз. Как раз
благодаря воображению из неё можно почерпнуть много информации.

Развёртка четырёхмерного куба

Сделать анимированный процесс разворачивания гиперкуба
хоть сколько нибудь наглядным просто невозможно. Но этот
процесс можно представить. (Для этого надо посмотреть на него
глазами четырёхмерного существа.)

Развёртка выглядит так.

Здесь видны все восемь кубов, ограничивающих гиперкуб.

Одинаковыми цветами покрашены грани, которые должны совместиться
при сворачивании. Серыми оставлены грани для которых парных не видно.
После свёртки самая верхняя грань верхнего куба должна совместиться
с нижней гранью нижнего куба. (Аналогично сворачивается развёртка
трёхмерного куба.)

Обратите внимание, что после свёртки все грани восьми кубиков
придут в соприкосновение, замкнув гиперкуб. И наконец, представляя
процесс свёртывания, не забывайте, что при свёртывании происходит не наложение
кубов, а оборачивание ими некой (гиперкубической) четырёхмерной области

Сальвадор Дали (1904-1989) много раз изображал распятие, а кресты
фигурируют в очень многих его картинах. На картине
«Распятие» (1954)
используется развёртка гиперкуба.

Кубик в кубе.

Кинематограф сегодня является неотъемлемой частью культуры. Ведь кто же не любит киноискусство в самых разных его проявлениях? С каждым годом на киноэкраны выходит все большее количество интересных и увлекательных кинолент, а количество поклонников этого вида искусства только увеличивается. Современные технологии позволяют каждому любителю киноискусства наслаждаться просмотром любого кинофильма или телесериала, не выходя из дома. А используя возможности киносайта, это занятие становится максимально комфортным. Сериалы кубик в кубе – прекрасное качество изображения и озвучки. Гости онлайн кинотеатра познакомятся с новинками кинолент с помощью анонсов и трейлеров, размещаемых на киносайте. Большой каталог, представленный на киносайте – это удобный онлайн просмотр кинокартин и телесериалов, как зарубежного, так и отечественного производства. Сайт позволяет произвести быстрый поиск и сделать легкий выбор кинокартин, которые порадуют гостей виртуального кинотеатра. А перевод кубик в кубе станет приятным дополнением к уже перечисленным преимуществам. Регулярно обновляемые подборки по жанрам кинофильмов и алфавитный указатель сериалов, позволят вам быстро найти интересующее видео.

На киносайте представлены последние новинки киноиндустрии в различных жанрах, от фантастических блокбастеров и трогательных комедий до леденящих душу триллеров и романтических мелодрам. Увлекательные приключения и запутанные детективные истории перенесут гостей виртуального кинозала в мир необыкновенных сюжетов и логических загадок. Также онлайн кинотеатр располагает большим выбором телесериалов на любой вкус. Одним из разделов коллекции киносайта являются познавательные исторические и документальные сериалы. Теперь вам больше не придется беспокоиться о пропуске любимой серии сериала. Фильмотека киносайта включает в себя обширную базу разнообразных многосерийных кинокартин. А каждая серия в озвучке кубик в кубе порадует вас своим качеством.

На киносайте помимо громких премьер и многосерийной телепродукции представлены киноленты прошлых лет. Если вы отдаете предпочтение старой доброй классике, то вас порадует изобилие данной коллекции.

Онлайн кинотеатр – это уютный домашний виртуальный кинозал, где любой гость вместе с семьей и друзьями сможет комфортно провести досуг за чашкой ароматного чая.

1 кубометр: сколько метров, литров, вес

1 кубометр

Чтобы понять, сколько в кубометре метров, литров или других единиц измерений, нужно сначала понять, чтобы такое кубометр. Кубический метр — это единица объема пространственной фигуры. Другими словами, это емкость с шириной, длиной и высотой равными одному метру.

Сколько метров в кубометре?

Это вопрос интересный, даже с то зрения философии. «Какая философия?» — спросите вы, ведь это же математика.

• Дело в том, что кубометр — это единица измерения объема, а метр — это единица измерения длины.
• Поэтому это две единицы, которые несопоставимы между собой.  

Но можно сказать и по-другому, уже углубляясь в математические величины:

• По ребрам — 12 метров.
• 1 метр — длины, ширины и высоты.
• 6 м² — площадь одной грани или площадь куба.
• Если разрезать кубическую фигуру на полосы и от толщины этих полос будет зависеть, сколько метров в кубическом метре. Например, если сечение метра квадратное и равно 1х1 см, то это ровно 10000 метров. Если сечение толщиной 10х10 см, то это 100 метров. Если разрезать на полоски шириной равной ширине человеческого волоса, то получится очень много метров.

Если формально связывать кубический метр (объем) и линейный размер (метр), то можно в косвенном смысле соотнести 1 кубометр и 1 метр. Но такое соотношение будет больше полезным для практического применения, а не для решения логических упражнений.

Ответ на этот вопрос простой: в одном кубометре 1000 литров.

1 кубометр

Вес кубометра

Сколько весит куб? Такой вопрос может возникнуть у любого человека. Но мало, кто знает и думает над тем, сколько килограмм в 1 куб. метре. Ответ: весовое значение будет зависеть от того, что находится в кубометре. Часто кубами измеряются, как сыпучие материалы (песок, щебенка), так и жидкости (H2O, кислота, спирт) и даже газообразные (газ). Пришла очередь разобраться по порядку:

• 1 куб. метр H2O — весовая величина будет зависеть от t°C: вода +20°С весит 998 кг, +4°С — одна тысяча кг.
• 1 куб. метр щебенки — зависит от характеристик и структурности камня. Кроме этого существует обычная плотность и насыпная плотность. Обычная плотность щебенки, гравия, гранита или известняка почти 2 раза больше, чем насыпная масса. Поэтому вес кубометра щебня будет равняться от 1,2 тонны до 2,6 тонны в зависимости от того, как уплотнен материал в кубическом метре.
• 1 куб. метр бетонного материала — зависит от свойств данного материала. Тяжелый бетон имеет вес 1,8-2,5 тонны (в зависимости от состава). Легкий бетон — 0,5 — 1,8 тонны.
• 1 куб. метр сыпучих материалов — зависит от составной величины и от наличия влаги в структуре. Вес песка, добытого в горах — 1,6 т, песок-перлит — 0,05-0,25 т, песка, добытого со дна реки — 1,4 — 1,86 т.
• 1 куб. метр древесного ствола или готового изделия — зависит от породы или наличия влаги. Чаще в строительстве применяется сосновые доски, брус и так далее, и именно строителям может понадобиться рассчитать, сколько в кубометре килограмм сосновых изделий. Свежесрезанный сосновый ствол — 0,8 т, полностью высушенная сосновая доска — 0,47 т.
• 1 куб. метр газа — вес этого материала найти невозможно, так как метан легче воздуха. Но можно измерить массу газа. В 1 кубе метана имеется 4,46 молей газа. Его молярная масса 16. Теперь вычисления: 4,46 х 16 = 71 грамм — масса газа.

Стоит отметить, что нет ответа на вопрос, сколько весит один кубометр. Это все равно что спросить — какая длина 1 килограмма, то есть все относительно. Если быть уверенным в том, какой материал находится в кубе, то можно измерить его величину веса, и она будет зависеть от различных физических и химических показателей.

Настройка фиксированной камеры

В OpenGL при использовании фиксированного конвейера есть ровно две матрицы, относящихся к трансформациям точек и объектов:

• GL_PROJECTION моделирует ортографическое или перспективное преобразование от трёхмерной усечённой пирамиды (т.е. от области видимости камеры) к трёхмерному кубу с длиной ребра, равной 2 (т.е. к нормализованному пространству).
• GL_MODELVIEW сочетает в себе два преобразования: от локальных координат объекта к мировым координатам, а также от мировых координат к координатам камеры.

За рамками фиксированного конвейера можно использовать столько матриц, сколько захочется — но сейчас мы ограничены. Кроме того, нам приходится смешивать матрицы:

• поведение камеры описывается как ортографическим или перспективным преобразованием, так и положением камеры в мировом пространстве, то есть для моделирования камеры нужны GL_PROJECTION и GL_MODELVIEW одновременно
• c другой стороны, для трансформаций над телами — например, вращения куба с помощью умножения координат на матрицу — нам нужна матрица GL_MODELVIEW.

Обычно при программировании действуют так:

• матрицу GL_PROJECTION обычно настраивают один раз для перспективного преобразования
• матрицу GL_MODELVIEW постоянно модифицируют, когда локальная система координат очередного объекта не совпадает с мировой системой координат

Начнём настройку камеры с GL_MODELVIEW: зададим матрицу так, как будто бы камера смотрит с позиции на точку , при этом направление “вверх” камеры задаёт вектор :

Для перспективного преобразования достаточно создать матрицу с помощью функции . Она принимает на вход несколько удобных для программиста параметров преобразования: горизонтальный угол обзора камеры (англ. field of view), соотношение ширины и высоты (англ. aspect), а также две граничных координаты для отсечения слишком близких к камере и слишком далёких от камеры объектов. Для лучшего понимания взгляните на иллюстрацию:

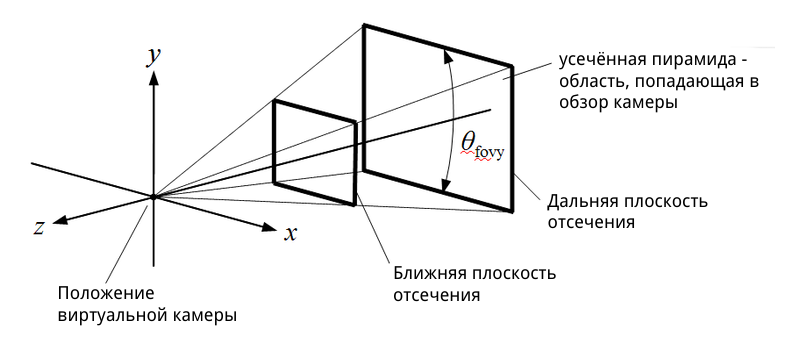
Однородное представление точек и векторов.

Давайте будем считать, что трёхмерная точка хранится как четырёхкомпонентный вектор . А вектор хранится как . Всего лишь одно флаговое значение в конце позволяет избежать любых ветвлений в алгоритмах трансформации векторов и точек. Это происходит благодаря свойствам алгебры матриц.

Как известно, можно умножить матрицу на матрицу при условии, что ширина одной матрицы равна высоте другой (иначе операция просто недопустима). Для получения элемента с позицией i,j в новой матрице достаточно взять i-ю строку левой матрицы и j-й столбец правой матрицы. Вот пример:

Как ни странно, умножение 4-х компонентного вектора на матрицу 4×4 тоже возможно! Для этого достаточно считать 4-х компонентный вектор матрицей 4×1. После умножения получится новый 4-х компонентный вектор.

Ещё более удивительно, что любую комбинацию трёхмерных перемещений, поворотов, вращений (и не только их!) можно представить как всего лишь одну матрицу 4×4, называемую матрицей трёхмерной трансформации. При этом умножение матрицы на трёхмерную точки или вектор, записанный в однородном представлении, даёт новую точку или вектор именно так, как этого требуют правила преобразования точек и векторов. Никаких ветвлений, и никакой магии!

Вершины куба

В чём OpenGL измеряет расстояния в трёхмерном мире? В 2D графике всё понятно: у нас есть пиксели. На трёхмерной проекции объекты одинакового размера могут дать разные проекции из-за перспективного искажения: чем дальше поверхность или линия, тем она меньше. Поэтому OpenGL измеряет расстояния в единицах измерения, не уточняя, в каких именно. Вы можете измерять в метрах, попугаях или в футах — на картинке это не имеет разницы, потому что исходные размеры не совпадают с проекциями.

Кроме того, трёхмерные тела поддаются преобразованиям. Поэтому мы будем рисовать только единичный куб и не станем заботиться о поддержке масштаба, вращения и положения центра куба. Единичный куб лежит в координатах от -1 до +1, т.е. каждое ребро имеет длину 2.

Изменения в CWindow

Теперь класс CWindow должен хранить три объекта:

Конструктор CCamera требует два аргумента, их можно задать следующим образом:

CWindow::CWindow()
: m_camera(CAMERA_INITIAL_ROTATION, CAMERA_INITIAL_DISTANCE)
{
SetBackgroundColor(QUIET_GREEN);
}

В методе Draw немного схитрим: применим вызов glTranslate (вместо нормальной работы с функциями GLM), чтобы развести два куба в стороны:

Метод SetupView станет проще, потому что мы можем не вычислять матрицу GL_MODELVIEW, а получить её начальное (для кадра) значение у камеры.

Наконец, следует перегрузить методы OnKeyDown/OnKeyUp класса CAbstractInputControlWindow в классе CWindow:

Секреты изготовления простого объёмного кубика

Когда в доме вдруг оказался нужен кубик, нет ничего проще, чем сделать его из бумаги. Способов сборки несколько.

Как сделать куб из бумаги: схема развёртки

Развёртка — это простая схема, которая позволит собрать объёмное изделие из материала. Развёртку-кубик можно распечатать, склеить или сделать самостоятельно.

Инструкция по изготовлению

Определимся, какой кубик мы хотим собрать из бумаги или картона, а может, вам хочется сделать своими руками куб с фотографиями?

Как сделать кубик из бумаги

Как сделать кубик из бумаги по схеме? Её легко и просто скачать и распечатать. Затем можно следовать простым инструкциям и получить желанный результат.

Для создания развёртки самостоятельно готовят бумагу, простой карандаш, линейку и ножницы. Так как у куба каждая сторона квадратная, то и чертить нам нужно квадраты с идеально ровными прямыми углами.

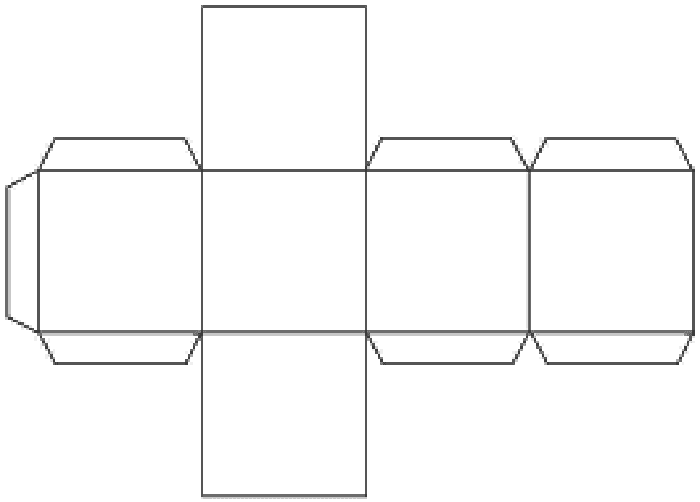
Шаблон кубика из бумаги можно распечататьФОТО: fs-center.ru

У любого куба 6 граней, потому и в схеме их должно быть ровно шесть. Сначала чертим центральный квадрат желаемой ширины (помним о том, что возможности А4 не безграничны), а вокруг него вычерчиваем ещё 4 квадрата с той же длиной стороны. Последний квадрат чертим сборку на любом элементе

Кроме граней, требуются припуски для склеивания. Их чертим сбоку, пририсовывая их к трём боковинам. Каждый припуск не должен быть свыше 1 см. Не забываем, что на припусках подрезаются уголки в 45º.

Получается кубФОТО: pinterest.com

Можно взять ножницы и вырезать всё по линиям. Грани будущего куба сгибаем. Все припуски тоже аккуратно сгибаются и промазываются клеем. Теперь остаётся только склеить все детали и дать изделию подсохнуть.

Как сделать из картона кубик

Разбираемся, как сделать своими руками кубик из картона.

Разница в изготовлении куба из бумаги и картона только в том, что сначала мы делаем развёртку из бумаги, если картон очень плотный. Это поможет избежать ошибок и неаккуратности. Никто не запрещает наносить разметку сразу на изнаночную сторону картона.

Вот как сделать куб из картонаФОТО: shkolala.ru

Фотокубик своими руками: креативный фотоальбом

А как сделать своими руками кубик с фотографиями? Это креативная головоломка, которая позволяет собрать разные фотографии.

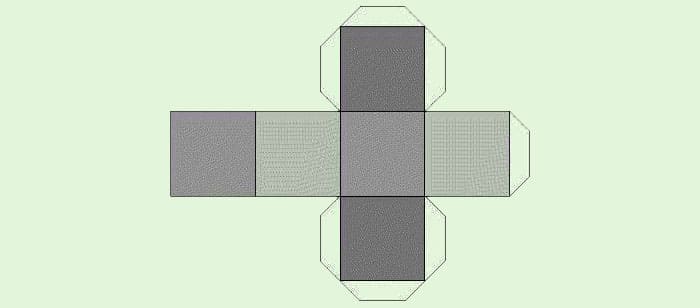
Схема кубика из картона своими руками абсолютно идентична схеме бумажного аналога и может быть воспроизведена даже ребёнкомФОТО: syl.ru

Чтобы сделать забавный фотоальбом на кубе-трансформере, нужно на каждую его грань приклеить кусочек фотографии или картинки.

В работе пользуются клеем, готовыми собранными из картона кубиками (грани по 4 см), скотчем.

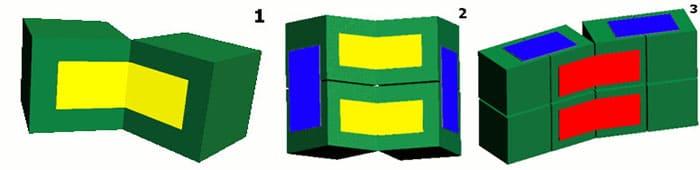
Чтобы трансформация удалась, нужно правильно склеивать кубикиФОТО: livemaster.ru

Фотографии лучше распечатать, чтобы они совпали размером. Изображение нужно взять с размерами 8×8 см². Можно сразу сделать разлиновку линией шириной в 1 пиксель: по ней легко будет резать после распечатывания, а сама линия будет незаметной.

Если берём 8 кубов, то требуется приготовить 10 фотографий. Картинка разрезается на 4 части по выделенной линии, и каждый элемент приклеивается на грань. Но до этого требуется сначала наклеить определённым образом полоски двустороннего скотча.

Фотографии должны быть приклеены максимально аккуратноФОТО: babyblog.ru

Изготовление оригами

Существует два варианта выполнения кубиков в стиле оригами:

1. Простой.
2. Сложный.

Для выполнения простого варианта вам понадобятся 6 листов бумаги формата А4. Каждый из листов необходимо превратить в квадрат, то есть, отрезать лишнюю часть листа. Из каждого листа необходимо сделать заготовку. Она выполняется в несколько этапов:

1. Согните квадратный лист на 4 равные части.
2. Верхний правый и нижний левый угол необходимо согнуть так, чтобы он касался соседней линии сгиба.
3. Сложите края заготовки к центру, и заправьте верхние и нижние уголки в получившиеся кармашки.
4. Полученную заготовку в виде параллелограмма, необходимо перевернуть и согнуть по линиям.
5. Получившиеся заготовки необходимо соединить друг с другом.
6. В каждом модуле есть специальные кармашки. Именно в них необходимо вставлять соседние модули.

Этот вариант выполнения поделки очень простой. На него у вас уйдёт не более трёх минут. Есть ещё один вариант выполнения кубика. Он более сложный. Суть в том, что там гораздо больше шагов, и очень просто запутаться. Новичок может потратить на выполнение такого варианта кубика 10—15 минут. Для его выполнения вам понадобится лишь квадратный лист бумага. Так, пошаговая инструкция выполнения этого куба:

1. Возьмите квадратный лист бумаги и сложите его по диагонали. После чего необходимо сложить его по другой диагонали.
2. Возьмите края половинных сгибов и соедините их вместе. Ваши диагональные сгибы должны оказаться на краю, а лист бумаги должен стать треугольным.
3. Прижмите получившуюся заготовку так, чтобы она была плоской.
4. Поверните заготовку открытой частью к себе.
5. Возьмите один нижний угол и согните его до верхнего края.
6. Повторите это действие для всех четырёх углов.
7. У вас получится 4 маленьких треугольника.
8. Необходимо верхушку каждого из них согнуть к центральной линии вашей заготовки.
9. Возьмите уголок, согнутый к верхушке. Согните его вниз. Это нужно для того? чтобы потом можно было заправить его в карман, который у нас получился в нижнем треугольнике.
10. Повторите это действие для всех четырёх уголков.
11. Раскройте вашу заготовку. Если смотреть на неё сверху, то вы должны видеть букву х.
12. Подуйте в дырочку, и тогда ваш кубик надуется.

Элементы гиперкуба

Гиперкуб размерности n имеет 2n «сторон»
(одномерная линия имеет 2 точки; двухмерный
квадрат — 4 стороны; трехмерный куб — 6 граней;
четырехмерный тессеракт — 8 ячеек).
Количество вершин (точек) гиперкуба равно 2n
(например, для куба — 23 вершин).

Количество m-мерных гиперкубов на
границе n-куба равно

Например, на границе гиперкуба находятся 8
кубов, 24 квадрата, 32 ребра и 16 вершин.

Элементы гиперкубов

n-куб	Название	Вершина(0-грань)	Ребро(1-грань)	Грань(2-грань)	Ячейка(3-грань)	(4-грань)	(5-грань)	(6-грань)	(7-грань)	(8-грань)
0-куб	Точка	1
1-куб	Отрезок	2	1
2-куб	Квадрат	4	4	1
3-куб	Куб	8	12	6	1
4-куб	Тессеракт	16	32	24	8	1
5-куб	Пентеракт	32	80	80	40	10	1
6-куб	Хексеракт	64	192	240	160	60	12	1
7-куб	Хептеракт	128	448	672	560	280	84	14	1
8-куб	Октеракт	256	1024	1792	1792	1120	448	112	16	1
9-куб	Эненеракт	512	2304	4608	5376	4032	2016	672	144	18