Предел складывания бумаги

Сколько раз можно сложить очень тонкую бумагу?

Некоторые люди заявляют что калька формата 520×380 мм без усилий складывается восемь раз, с усилиями — девять. При этом каждый из сгибов должен быть перпендикулярен предыдущему. Если сгибать под другим углом, можно добиться того, что количество сгибаний будет чуть большим (но не всегда).

Очень тонкая калька может быть толщиной 37-47 микрон.

Калька — своего рода аналог множества «слоёв» в компьютеризированном черчении. Это тонкая прозрачная бумага, применяемая при черчении и ручном копировании.

Обычная бумажная салфетка складывается 8 раз, если нарушить условие и один раз сложить не перпендикулярно предыдущему.

Студенты сложили бумагу 13 раз

Студенты-математики из США сложили туалетную бумагу 13 раз, что ранее считалось почти невозможным. На то чтобы установить весьма своеобразный мировой рекорд, у учащихся Школы Святого Марка (St. Mark’s School) ушло без малого семь часов.

Напомним, что с каждым сложением толщина нового «бумажного листа» возрастает вдвое, а загибы становятся всё более округлыми, складывать становится всё труднее и труднее. Кроме всего прочего, мешают складки, образующиеся на самой бумаге. Из-за всех этих неприятных «побочных эффектов» листы почти невозможно сложить больше определённого количества раз, сколько силы не прикладывай (рвать их нельзя).

Молодые учащиеся американской школы не без помощи учителей вывели формулу, учитывающую толщину бумажного листа и выдающую в результате длину ленты, необходимой для завершения важной миссии (складывания в определённое количество раз).  

Так как ни один существующий рулон туалетной бумаге не имеет подходящую длину ленты, студентам пришлось склеить между собой в единое полотно несколько промышленных рулонов туалетной бумаги (длиной 1,2 километра каждый).

В результате ими была сложена конструкция, которая состояла из 8192 слоёв туалетной бумаги общей протяжённостью 16 километров. 13 сложений даже стабильно держали форму, хотя в высоту такой «рулон» достигал 76, а в ширину и вовсе 150 сантиметров.

«Разрушители Легенд» сложили бумагу 11 раз

К слову, в известной телепередаче «Разрушители Легенд» был поставлен эксперимент по многократному складыванию бумаги. В ходе данного эксперимента использовался лист бумаги размером с футбольное поле, а сгибали его с помощью тяжелой строительной и дорожной техники. Каждый следующий изгиб делался перпендикулярно предыдущему. По результатам эксперимента удалось сложить бумагу 11 раз. Таким образом, легенда о максимально возможных семи складываниях листа бумаги была разрушена, не только теоретически, но в том числе и на практике.

https://youtube.com/watch?v=kRAEBbotuIE

Команда исследователей «Разрушители легенд» попыталась опровергнуть закон. Они сформулировали его более точно: Даже очень большой сухой лист бумаги нельзя сложить вдвое больше семи раз, делая каждый из сгибов перпендикулярно предыдущему.

На обычном листе А4 закон подтвердился, тогда исследователи проверили закон на огромном листе бумаги. Лист размером с футбольное поле (51,8×67,1 м) им удалось сложить 8 раз без специальных средств (11 раз с применением катка и погрузчика).

Школьница которая смогла сложить бумагу 12 раз

В 2001 году одна американская школьница решила вплотную заняться проблемой двойного складывания, а получилось из этого целое научное исследование, да ещё и мировой рекорд.

Собственно, началось всё с вызова, брошенного педагогом ученикам: «А вот попробуйте сложить хоть что-нибудь пополам 12 раз!». Мол, убедитесь, что это из разряда совершенно невозможного.

Бритни Гэлливан (Britney Gallivan) поначалу отреагировала как Алиса Льюиса Кэрролла: «Бесполезно и пробовать». Но ведь говорила Алисе Королева: «Осмелюсь сказать, что у вас не было большой практики».

Вот Гэлливан и занялась практикой. Порядком намучившись с разными предметами, она сложила-таки лист золотой фольги вдвое 12 раз, чем посрамила своего преподавателя.

На этом девушка не успокоилась. В декабре 2001 года она создала математическую теорию (ну, или математическое обоснование) процесса двойного складывания, а в январе 2002 года проделала 12-кратное складывание пополам с бумагой, используя ряд правил и несколько направлений складывания.

Мировая рекордсменка Бритни Гэлливан и бумажная лента, сложенная вдвое (в одном направлении) 11 раз

Бритни заметила, что к этой проблеме ранее уже обращались математики, но правильного и проверенного практикой решения задачи ещё никто не предоставлял.

Гэлливан стала первым человеком, который правильно понял и обосновал причину ограничений на сложение. Она изучила накапливающиеся при складывании реального листа эффекты и «потерю» бумаги (да и любого иного материала) на сам сгиб. Она получила уравнения для предела складывания, для любых исходных параметров листа.

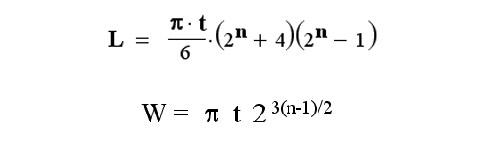уравнения для предела складывания, для любых исходных параметров листа

Первое уравнение относится к складыванию полосы только в одном направлении. L — минимально возможная длина материала, t – толщина листа, и n — число выполненных сгибов в два раза. Разумеется, L и t должны быть выражены в одних и тех же единицах.

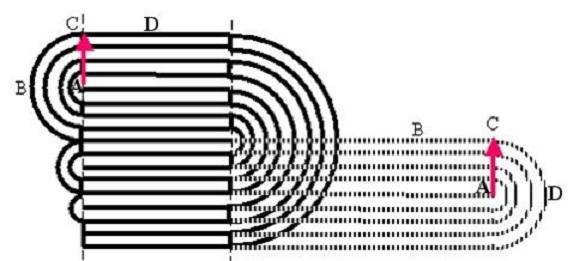Пример складывания листа вдвое четыре раза. Пунктир – предыдущее положение трёхкратного сложения. Буквы показывают, что точки на поверхности листа смещаются (то есть, листы скользят друг относительно друга), и занимают в результате не то положение, как может показаться при беглом взгляде

Во втором уравнении речь идёт о складывании в различных, переменных, направлениях (но всё равно – вдвое каждый раз). Здесь W – ширина квадратного листа. Точное уравнение для складывания в «альтернативных» направлениях – более сложное, но здесь приводится форма, дающая очень близкий к реальности результат.

Для бумаги, которая не является квадратом, вышеупомянутое уравнение всё ещё даёт весьма точный предел. Если бумага, скажем, имеет пропорции 2 к 1 (по длине и ширине), легко сообразить, что нужно сложить её один раз и «привести» к квадрату двойной толщины, а затем воспользоваться вышеупомянутой формулой, мысленно держа в уме одно лишнее складывание.

В своей работе школьница определила строгие правила двойного сложения. Например, у листа, который свёрнут n раз, 2n уникальных слоёв обязаны лежать подряд на одной линии. Секции листа, не удовлетворяющие этому критерию, не могут считаться как часть свёрнутой пачки.

Так вот Бритни и стала первым в мире человеком, сложившим лист бумаги вдвое 9, 10, 11 и 12 раз. Можно сказать, не без помощи математики.

Похожее

Выпадение орла или решки можно точно предсказать
Орел или решка? При определенных условиях результат бросания монеты можно точно предсказать. Этими определенными условиями, как показали недавно польские физики-теоретики, являются высокая точность в задании начального положения и скорости падения монеты.

О математике
Губин В. Б.
Математика изучает принципы и результаты деятельности вообще, как бы вырабатывая заготовки для описания реальной деятельности и ее результатов, и в этом заключается один из источников ее универсальности.

Каустики на плоскости и в пространстве

Каустики — это вездесущие оптические поверхности и кривые, возникающие при отражении и преломлении света. Каустики можно описать как линии или поверхности, вдоль которых концентрируются световые лучи.

Алгебраическая структура пространства-времени, алгебродинамика полей и частиц
Вашему вниманию предлагается исследовательская программа, последовательно возрождающая неопифагорейскую философию в теоретической физике и основанная на убеждении в неслучайности физических законов, в существовании единого первичного принципа, определяющего структуру (видимого и невидимого) Мира и записанного на абстрактном математическом языке, на языке Чисел (целых, действительных и, возможно, их обобщений).

Научное воображение
Ричард Фейнман
Представьте себе электрические и магнитные поля. Что вы для этого сделали? Знаете ли вы, как это нужно сделать? И как я сам представляю себе электрическое и магнитное поля? Что я на самом деле при этом вижу? Что требуется от научного воображения? Отличается ли оно чем-то от попытки представить себе комнату, полную невидимых ангелов? Нет, это не похоже на такую попытку.

Квантовая математика
Программа Гордона
Что характеризует «квантовую», или «некоммутативную», математику, которая на самом деле родилась вместе с квантовой механикой, но никто этого не заметил? Каким образом квантовая математика пыталась помирить двух великих физиков, да не смогла? О том, почему «настоящая» теорема отвечает не только на поставленный вопрос, но и на ряд еще не поставленных, — доктор физико-математических наук, профессор МГУ Александр Хелемский.

Популярно о работах Якова Синая, лауреата Абелевской премии 2014 года
26 марта в Осло президент Норвежской академии наук объявил имя лауреата Премии Абеля за 2014 год — аналога Нобелевской премии по математике. Им стал выдающийся ученый, представляющий Россию и США, Яков Григорьевич Синай.

Чем определяется предельный размер гигантских дюн в пустыне?
Юрий Ерин

Известно, что рост гигантских дюн происходит за счет поглощения более мелких дюн и, казалось бы, ничто не мешает принимать им сколь угодно большие размеры. Французским ученым из Лаборатории физики и механики неоднородных сред в сотрудничестве с исследователями из США и Алжира удалось установить, что этот процесс ограничен глубиной так называемого приповерхностного атмосферного слоя, который определяет характер течения воздуха над гигантскими дюнами.

Солитоны
Голубев А.
Человеку даже без специального физического или технического образования несомненно знакомы слова «электрон, протон, нейтрон, фотон». А вот созвучное с ними слово «солитон» многие, вероятно, слышат впервые

Это и неудивительно: хотя то, что обозначается этим словом, известно более полутора столетий, надлежащее внимание солитонам стали уделять лишь с последней трети XX века. Солитонные явления оказались универсальными и обнаружились в математике, гидромеханике, акустике, радиофизике, астрофизике, биологии, океанографии, оптической технике

Что же это такое – солитон?

Гипотеза математической вселенной
Согласно гипотезе, наша внешняя физическая реальность является математической структурой. То есть, физический мир является математическим в определённом смысле. Все математические структуры, которые можно вычислить, существуют. Гипотеза предполагает, что миры, соответствующие различным наборам начальных состояний, физических констант, или совсем других уравнений, можно рассматривать как одинаково реальные.

Далее >>>

Рассуждения и вычисления про складывание бумаги

Если вы попытаетесь соблюдать эти условия, то скорее всего и правда не получится сложить бумагу более 7 раз. Но это не говорит о полной невозможности данного факта.

Читайте дальше и вы многое поймёте о том что другие не в силах объяснить. Если вы любите короткие факты на 2 предложения без истории, бэкграунда и размышлений, то не утруждайте себя, и пусть для вас на всю жизнь останется непоколебимой истиной тот факт, что бумагу нельзя сложить более 8 раз.

Существует миф, что один лист бумаги нельзя сложить более семи раз так, чтобы линия каждого последующего изгиба была перпендикулярна линии предыдущего изгиба. Однако это не правда.

Нет никаких фундаментальных законов физики, которые бы запрещали сложить лист бумаги подобным образом в восьмой и последующие разы. Однако для этого понадобится очень много бумаги. Дело в том, что при каждом таком складывании листа бумаги его толщина удваивается. Поэтому, если принять начальную толщину листа бумаги за 0,1 мм = 0,0001 метр (а это абсолютно реалистично), то можно записать такую формулу для толщины (H) сложенного листа бумаги после N складываний:

H = 0,0001∙2N метров

Простыми словами:

1 Складывание – 0.1 сантиметра∙2 = 0.2 сантиметра

2 Складывание — 0.2 сантиметра∙2 = 0.4 сантиметра

3 Складывание — 0.4 сантиметра∙2 = 0.8 сантиметра

4 Складывание — 0.8 сантиметра∙2 = 1.6 сантиметра

5 Складывание — 1.6 сантиметра∙2 = 3.2 сантиметра

6 Складывание — 3.2 сантиметра∙2 = 6.4 сантиметра

7 Складывание — 6.4 сантиметра∙2 = 12.8 сантиметра

8 Складывание — 12.8 сантиметра∙2 = 25.6 сантиметра

9 Складывание — 25.6 сантиметра∙2 = 51.2 сантиметра

10 Складывание — 51.2 сантиметра∙2 = 102.4 сантиметра

20 Складывание — 104857,6 сантиметра — 1048,576 метров – 1.05 километра

Даже на 5-6 складывании становится понятно, что стопку бумаги в несколько сантиметров очень трудно сложить.

Таким образом, хотя никакие законы физики не запрещают много раз складывать бумагу, тем не менее понятно, что у того, кто захочет поставить подобный эксперимент, очень быстро закончится бумага и возможность изгибать такие толстые стопки бумаги, не разорвав её.

Кстати расстояние от Земли до Луны 384 400 километров.

Давайте рассуждать. Каждое сложение удваивает толщину кипы. Если толщину бумаги принять равной 0,1 миллиметра (размер листа мы сейчас не рассматриваем), то сложение её вдвое «всего» 51 раз даст толщину сложенной пачки в 226 миллионов километров. Что уже очевидный абсурд.

Кажется, тут-то мы начинаем понимать, откуда берётся известное многим ограничение на 7 или 8 раз (ещё раз – бумага у нас реальная, она не тянется до бесконечности и не рвётся, а порвётся – это уже не складывание).

Что показывает пример со складыванием бумаги?

Выражение «экспоненциальный рост» вошло в наш лексикон для обозначения быстрого, как правило безудержного увеличения. Оно часто используется, например, при описании стремительного роста числа городов или увеличения численности населения. Однако в математике этот термин имеет точный смысл и обозначает определенный вид роста.

Экспоненциальный рост – это, когда мы умножаем следующую получившуюся сумму на 2.

В отличие от линейного роста, который является результатом многократно добавления постоянной, экспоненциальный рост – это многократное умножение. Если линейный рост – это стабильная во времени прямая линия, то линия экспоненциального роста похожа на взлет. Чем большее значение принимает величина, тем быстрее она растет дальше.

Представьте, что вы идете по дороге, и каждый ваш шаг получается метр в длину. Вы делаете шесть шагов, и теперь вы продвинулись на шесть метров. После того, как вы сделаете еще 24 шага, вы окажетесь в 30 метрах от того места, где вы начали. Это линейный рост.

А теперь представьте (хотя ваше тело так не умеет, но представьте), что каждый раз длина вашего шага увеличивается вдвое. То есть сначала вы шагаете на один метр, затем на два, затем на четыре, затем на восемь и так далее. За шесть таких шагов вы преодолеете 32 метра – это гораздо больше, чем за шесть шагов по одному метру. В это трудно поверить, но если продолжать в том же темпе, то после тридцатого шага вы окажетесь на расстоянии миллиарда метров от исходной точки. Это 26 поездок вокруг Земли. И это экспоненциальный рост.

Чтобы лучше понять, что такое экспоненциальный рост, представьте себе популяцию, состоящую изначально из одной бактерии. Через определенное время (через несколько часов или минут) бактерия делится надвое, тем самым удваивая размер популяции. Через следующий промежуток времени каждая из этих двух бактерий снова разделится надвое, и размер популяции вновь удвоится — теперь будет уже четыре бактерии. После десяти таких удвоений будет уже более тысячи бактерий, после двадцати — более миллиона, и так далее. Если с каждым делением популяция будет удваиваться, ее рост будет продолжаться до бесконечности.

Существует легенда (скорее всего, не соответствующая действительности), будто бы человек, который изобрел шахматы, доставил этим такое удовольствие своему султану, что тот пообещал исполнить любую его просьбу. Человек попросил, чтобы султан положил на первую клетку шахматной доски одно зерно пшеницы, на вторую — два, на третью — четыре и так далее. Султан, посчитав это требование ничтожным по сравнению с оказанной им услугой, попросил своего поданного придумать другую просьбу, но тот отказался. Естественно, к 64-му удвоению число зерен стало таким, что во всем мире не нашлось бы нужного количества пшеницы, чтобы удовлетворить эту просьбу. В той версии легенды, которая известна мне, султан в этот момент приказал отрубить голову изобретателю. Мораль такова: иногда не следует быть чересчур умным!

Примеры показывают нам, что никакая популяция не может расти вечно. Рано или поздно она попросту исчерпает ресурсы — пространство, энергию, воду, что угодно. Поэтому популяции могут расти по экспоненциальному закону лишь некоторое время, и рано или поздно их рост должен замедлиться.

Значит у такого роста могут быть логические ограничения, не связанные с ограничениями законами физики.

Заключение

Как подсказывает умная Википедия, предел складывания бумаги пополам — физический феномен, суть которого состоит в том, что лист обычной бумаги размера А4 можно сложить пополам не более 7 раз. Он происходит из-за быстроты роста показательной функции и экспоненциального роста.

Количество слоёв бумаги равняется двум в степени n, где n — количество складываний бумаги. Например: если бумагу сложили пополам пять раз, то количество слоёв будет два в степени пять, то есть тридцать два.

Итак, сложить обычный лист бумаги 7 или 8 раз, при помощи рук, практически невозможно. Но если это очень тонкая бумага или очень большой кусок бумаги то можно сложить более 7 раз. Так же не стоит забывать про правила и условия. Например про влажность тоже нужно помнить.

http://mathworld.wolfram.com/Folding.html

http://www.membrana.ru/particle/2335

https://nauka.vesti.ru/article/1035082

https://ru.wikipedia.org/