Смещение перигелия меркурия
Содержание:
- Литература
- Афелий Земли[править | править код]
- Примечания
- Как далеко Меркурий от Солнца?
- Орбита — окружность непростая…
- Абсолютная звездная величина
- Что такое перигелий?
- Видимая звездная величина
- Основные формулы
- Марс
- Фактор, отвечающий за смену времен года
- Терминология
- Афелий
- Решение в рамках общей теории относительности
- Меркурий в 2019 году
- Параллакс
Литература
- Богородский А. Ф. Всемирное тяготения. — Киев : Наукова думка, 1971. — 351 с.
- Визгин В. П. Релятивистская теория тяготения. Истоки и формирование. 1900—1915 гг. — М. : Наука, 1981. — 352 с.
- Климишин И. А. Релятивистская астрономия. — 2-е изд. — М. : Наука, 1989. — С. 35—41. — ISBN 5-02-014074-0.
- Роузвер Н. Т. Перигелий Меркурия. От Леверье до Эйнштейна = Mercury’s perihelion. From Le Verrier to Einstein. — М. : Мир, 1985. — 244 с.
- Субботин М. Ф. Введение в теоретическую астрономию. — М. : Наука, 1968. — С. 58—67.
- Earman J., Janssen M. Einstein’s Explanation of the Motion of Mercury’s Perihelion // The Attraction of Gravitation: New Studies in the History of General Relativity: Einstein Studies, Volume 5. — Boston : Birkhãuser, 1993. — С. 129—149. — 432 с. — ISBN 3764336242.
Афелий Земли[править | править код]
Средний афелий барицентра системы Земля-Луна составляет 152 098 233 километра (на эпоху J2000.0). Земля проходит афелий между 3 и 7 июля (через пару недель после летнего солнцестояния, однако это приблизительное совпадение случайно). Изменение даты прохождения афелия и колебание афелийного расстояния обусловлены возмущениями от Луны и (в меньшей степени) планет. На них накладывается также периодическое смещение календарного момента прохождения афелия в пределах одних суток, обусловленное високосным циклом. Долгота афелия барицентра системы Земля-Луна составляет −77,06231807° (долгота перигелия минус 180°) на эпоху J2000.0 и увеличивается со скоростью 0,32327364° за юлианское столетие (то есть за 35 525 суток СИ). Эксцентриситет земной орбиты в течение последних веков претерпевает постепенное уменьшение (со скоростью −0,00004392 за юлианское столетие), орбита приближается к круговой. Хотя большая полуось орбиты при этом растёт (5,62×10−6 а.е. за юлианское столетие), но этот прирост относительно более медленный, поэтому афелий, который равен произведению (1+e)a,{\displaystyle (1+e)a,} постепенно уменьшается на 38,3×10−6 а.е. (5,73 тыс. км) за юлианское столетие. Указанные изменения относятся к периоду 1800—2050 гг. н.э.; однако для более длительного промежутка времени (3000 до н.э. — 3000 н.э.) афелий характеризуется приблизительно таким же вековым уменьшением. Эти изменения являются частью гораздо более длительных, с характерным временем в десятки тысячелетий, периодических изменений элементов орбиты Земли.
В таблице указаны моменты прохождения афелия Землёй на 2010—2029 годы и расстояния от Солнца на эти моменты, вычисленные в рамках модели JPL DE405.
| Год | Дата | Время (UTC) | Расстояние (а.е.) | Отклонение от среднего афелия (км) |
|---|---|---|---|---|
| 2010 | 6 июля | 11:30 | 1,0167020 | −1246 |
| 2011 | 4 июля | 14:54 | 1,0167404 | 4501 |
| 2012 | 5 июля | 03:32 | 1,0166751 | −5270 |
| 2013 | 5 июля | 14:44 | 1,0167085 | −268 |
| 2014 | 4 июля | 00:13 | 1,0166816 | −4287 |
| 2015 | 6 июля | 19:40 | 1,0166821 | −4214 |
| 2016 | 4 июля | 16:24 | 1,0167509 | 6080 |
| 2017 | 3 июля | 20:11 | 1,0166756 | −5190 |
| 2018 | 6 июля | 16:47 | 1,0166961 | −2129 |
| 2019 | 4 июля | 22:11 | 1,0167543 | 6590 |
| 2020 | 4 июля | 11:35 | 1,0166943 | −2399 |
| 2021 | 5 июля | 22:27 | 1,0167292 | 2832 |
| 2022 | 4 июля | 07:11 | 1,0167154 | 760 |
| 2023 | 6 июля | 0:07 | 1,0166806 | −4444 |
| 2024 | 5 июля | 05:06 | 1,0167255 | 2273 |
| 2025 | 3 июля | 19:55 | 1,0166437 | −9957 |
| 2026 | 6 июля | 17:31 | 1,0166440 | −9920 |
| 2027 | 5 июля | 05:06 | 1,0167289 | 2786 |
| 2028 | 3 июля | 22:18 | 1,0166798 | −4566 |
| 2029 | 6 июля | 05:12 | 1,0167127 | 362 |
Примечания
- Комментарии
- Ранее «неправильное поведение» было отмечено у кометы Энке, видимо, из-за реактивной отдачи летучих веществ, и у Луны, см. Приливное ускорение, однако эти эффекты не вызывали сомнений в теории тяготения.
- Источники
- ↑ , с. 9—10.
- Фейнман Р. Характер физических законов. — Изд. 2-е. — М.: Наука, 1987. — С. 155. — 160 с. — (Библ. Квант, выпуск 62).
- , с. 65.
- ↑ , с. 17.
- Le Verrier U. Théorie de mouvement de Mercure (фр.) // Ann. Observ. imp. — 1859. — Vol. 5, 1—96.
- ↑ Isaac Asimov. (англ.) (May 1975). Дата обращения 6 мая 2014.
- ↑ Paul Schlyter. (англ.). Дата обращения 7 мая 2014.
- Richard Baum, William Sheehan. In Search of Planet Vulcan, The Ghost in Newton’s Clockwork Machine. — New York: Plenum Press, 1997. — ISBN 0-306-45567-6.
- , с. 7—8, 33—36, 46, 61—62.
- , с. 84—90, 97—117.
- , с. 61.
- , с. 37—39, 60.
- , с. 20—21, 31, 34, 47.
- , с. 54—55, 59—60.
- Hill H. A., Stebbins R. T. The intrinsic visual oblateness of the sun // Astrophys. Journal. — 1975. — Вып. 200. — P. 471—483.
- ↑ , с. 36—37.
- Гарцер П. Звезды и пространство. // Новые идеи в математике. СПб.: Образование, 1913, вып. 3, с. 71—116.
- , с. 98—116.
- Newcomb S. The elements of the four inner planets and the fundamental constants of astronomy. Suppl. am. Ephem. naut. Aim. 1897. U.S. Govt. Printing Office, Washington, D. C., 1895.
- ↑ , с. 49—51, 57—58.
- , с. 49—51, 57—63.
- , с. 35—58.
- , с. 19.
- Hall A. A suggestion in the theory of Mercury (англ.) // Astr. J. — 1894. — Vol. 14. — P. 49—51.
- Гравитационный парадокс // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 1. — ISBN 5-85270-034-7.
- , с. 65—67.
- Newcomb S. Discussion and results of observations on transits Mercury from 1677 to 1881. Astr. Pap. am. Ephem. naut. Aim., t, 367—487. U. S Govt. Printing Office, Washington, D. C., 1882.
- ↑ , с. 55—56.
- , с. 34—35.
- , с. 63.
- , с. 8, 44, 82—83, 89—90.
- ↑ , с. 139—161.
- , с. 44—49, 56—63.
- , с. 161—168.
- Gerber, P. Die räumliche und zeitliche Ausbreitung der Gravitation // Zeitschrift für Mathematik und Physik. — 1898. — Vol. 43. — P. 93–104.
- ↑ , с. 168—176.
- Макс фон Лауэ. О движении перигелия Меркурия (историко-критический очерк) // Лауэ М. Статьи и речи. — М.: Наука, 1969. — С. 86—89.
- , с. 179.
- Зелиг К. Альберт Эйнштейн. — 2-е изд. — М.: Атомиздат, 1966. — С. 74.
- ↑ , с. 180—186.
- Эйнштейн А. Объяснение движения перигелия Меркурия в общей теории относительности // Собрание научных трудов в 4 томах. — Т. I. — С. 439—447.
- Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 5-е, исправленное и дополненное. — М.: Наука, 1967. — 460 с. — («Теоретическая физика», том II)., § 98 «Движение в центрально-симметричном гравитационном поле».
- ↑ , с. 113—117.
- Kevin Brown. (англ.). Reflections on Relativity (2012). Дата обращения 14 апреля 2014.
- , с. 66.
- . Дата обращения 15 апреля 2014.
- Нарликар Дж. Гравитация без формул. — М.: Мир, 1985. — С. 88. — Тираж 50 000 экз.
- . European Southern Observatory.
Как далеко Меркурий от Солнца?
Перигелий и афелий
Средняя удаленность между планетой и звездой составляет 57 909 050 км. Но эксцентриситет – 0,205 (наибольший в нашей системе), поэтому дистанция может отличаться. Максимальная близость (перигелий) – 46 001 200 км, а отдаленность (афелий) – 57 909 050 км.
Орбитальный резонанс
Ранее полагали, что планета проживает в орбитальном блоке, то есть повернута к звезде одной стороной. Но оказалось, что осевой оборот достигает 58.646 дней, а на орбитальный уходит 88 дней. Это привело к резонансу в 3:2 (три осевых оборота на 2 орбитальных).
Кроме того, это повлияло на солнечный день. На проход Солнца по небу с позиции Меркурия уходит 176 дней. То есть, один день может занимать 2 года! Именно медленность вращения приводит к резким температурным скачкам.
Прецессия перигелия
Меркурий также подвергается прецессии. То есть, каждый век орбитальный путь сдвигается на 42.98 угловых секунд. Пройдет 12 миллионов орбит, планета выполнит дополнительный оборот и вернется в изначальную точку.
У других планет наблюдается похожая ситуация, но с меньшим показателем. Механика Ньютона не могла объяснить подобное поведение, поэтому до 20-го века мы не понимали, что происходит. Только с общей теорией относительности пришли ответы. Теперь вы знаете расстояние от Солнца до Меркурия — первой планеты Солнечной системы.
Полезные статьи:
Несколько дней назад мне прислали следующий вопрос:
Меркурий – ближайшая к Солнцу планета. Среднее расстояние от Солнца до Меркурия составляет примерно 57 миллионов километров. При этом в афелии, т.е. в точке наибольшего удаления Меркурия от Солнца это расстояние составляет почти 70 млн. километров, а в перигелии, т.е. в ближайшей к Солнцу точке орбиты – всего 49 млн. километров.
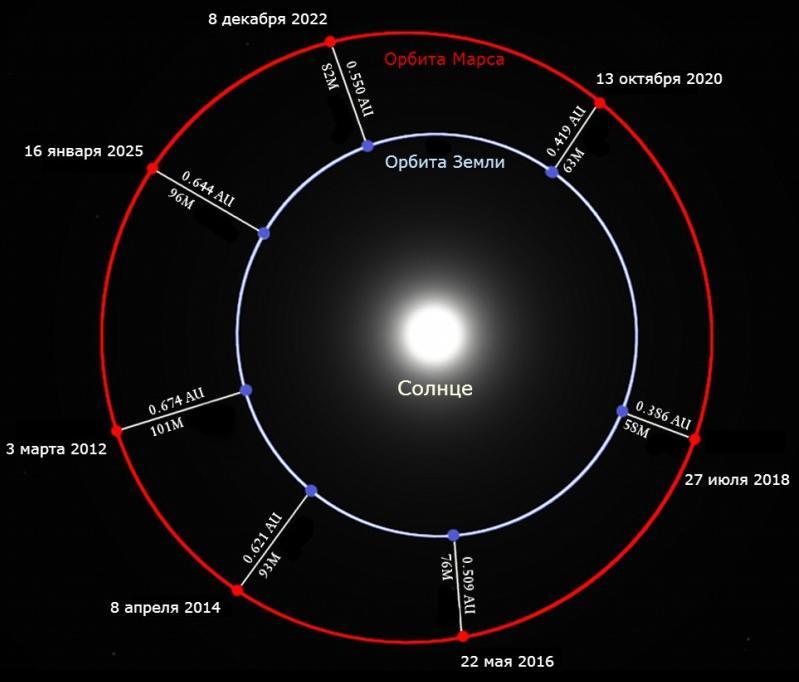
В 1859-м году французский астроном Убрен Леверье сделал интересное наблюдение: он обнаружил, что орбита Меркурия как-бы поворачивается вокруг Солнца. При этом происходит и смещение перигелия. Смещение на самом деле совсем небольшое — примерно на полторы угловых секунды за год, но все же достаточно заметное, чтобы его можно было обнаружить с помощью наблюдательной техники того времени.
Ну сделал себе и сделал такое наблюдение, казалось бы что тут такого? Но беда в том, что это смещение никак не вписывалось в рамки Ньютоновской классической механики. Вот хоть ты тресни, а по формулам Ньютона не должно быть никакого смещения, а оно есть.
Как только не пытались объяснить это смещение: и искали таинственную нулевую планету между Солнцем и Меркурием, даже дали ей имя Вулкан, и искали у Меркурия не открытые пока спутники, и пробовали пересчитать все по-ньютоновски поменяв немного массу Венеры и других планет (мало ли, вдруг ошибка вышла, когда «взвешивали»), некоторые астрономы даже предполагали наличие у Солнца кольца или колец на манер Сатурна, но все тщетно.
Ни одна из этих гипотез не нашла никаких подтверждений наблюдениями. А тут еще спустя 40 лет другой астроном – американец Саймон Ньюком возьми да и открой похожее смещение перигелия у Марса. Вообщем, неувязочка вышла, которую долго не знали как объяснить.
И тут-то и появился на сцене Эйнштейн со своими теориями относительности общей и специальной и говорит: «Сейчас, я вам все объясню». И таки объяснил. Как оказалось смещения перигелия орбиты Меркурия и Марса отлично объясняются теорией относительности. Более того аналогичные смещения перигелия есть и всех других планет, просто у Меркурия они наиболее заметны из-за большого эксцентриситета орбиты.
На сегодняшний момент идеально точное совпадение смещения перигелия орбиты Меркурия с данными рассчитанными на основе теории гравитации Эйнштейна является одним из наиболее важных и ключевых практических доказательств теории относительности.
Орбита — окружность непростая…
Всем людям с рождения известно о том, что космические тела, в первую очередь планеты, вращаются по орбите, представляющей собой круг. Но в данном случае это относительное понятие. Дело в том, что ни одна окружность, по которой космическое тело проходит свой путь вокруг Солнца, не является идеальной. В той или иной степени все они приближены к эллипсу. Такие искажения придают всем планетам дополнительную уникальную составляющую, ведь на каждом участке орбиты Солнце будет по-разному воздействовать на них, иногда в значительной степени оказывая влияние на климат и другие показатели. Особенно заметно это воздействие в двух точках. Каких?
Абсолютная звездная величина
Денеб – одна из самых больших звезд, известных науке, имеет звездную величину +1,25. Ее диаметр примерно равен диаметру орбиты Земли и больше диаметра Солнца в 110 раз. Расстояние до этого исполина – 1 640 световых лет. Хотя ученые еще спорят по этому вопросу, уж очень это далеко. Большинство звезд, находящихся на таком удалении, можно увидеть только в телескоп. Если бы мы были к этой звезде ближе, то и яркость Денеба на небе была бы куда выше. Тем самым видимая звездная величина зависит как от светимости объекта, так и от расстояния до него. Чтобы можно было сравнить светимость разных звезд между собой, используют абсолютную звездную величину. Для звезд она определяется как видимая звездная величина объекта, если бы он был расположен на расстоянии 10 парсек от наблюдателя. Если расстояние до звезды известно, то абсолютную звездную величину рассчитать несложно.
Абсолютная звездная величина Солнца составляет +4,8 (видимая, напомним, -26,7). Сириус – самая яркая звезда ночного неба – имеет видимую величину ?1,46, но абсолютную всего +1,4. Что, впрочем, неудивительно, ведь бриллиант ночного неба (как называют эту звезду) находится близко от нас: на расстоянии всего 8,6 световых лет. А вот абсолютная звездная величина уже упомянутого Денеба составляет -6,95.
Что такое перигелий?
Это точка, где планета, комета или астероид находятся на наименьшем расстоянии до солнца. Такие моменты для некоторых из них могут считаться полноценным летом, а для других могут и не приносить особых изменений.
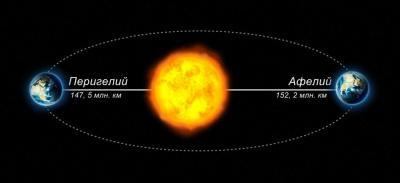
Например, у Земли различие между минимальной и максимальной дистанцией относительно небольшое, всего 5 млн км. Поэтому данные периоды люди даже не замечают. Однако для уточнения стоит отметить, что Земля проходит перигелий 4-5 января ежегодно. В северном полушарии в это время самый разгар зимы, а в южном — вполне обычное лето.
А если представить, что была бы возможность оказаться на Меркурии, то разницу можно было бы почувствовать, потому что его орбита гораздо сильнее отличается от ровного круга. Как и для Земли, моменты наибольшего сближения не являются актуальными для Венеры, Юпитера, Сатурна, Урана и Нептуна.
Видимая звездная величина
Количество звезд на ночном небе, доступных невооруженному взгляду, не так велико, как кажется. Если иметь хорошую остроту зрения и выбраться за город, подальше от уличного освещения, то для наблюдения будут доступны около 6000 звезд. При этом половина из них всегда будет скрыта от наблюдателя за горизонтом. Но даже этого количества достаточно, чтобы заметить, насколько звезды отличаются по своей яркости. Замечали это и античные ученые. Живший во II веке до нашей эры древнегреческий математик и астроном Гиппарх разделил все наблюдаемые им звезды на шесть величин. Самые яркие он отнес к первой величине, самые тусклые – к шестой.
В целом, этот принцип используется и сейчас. Но сегодня возможности астрономии позволяют наблюдать бесчисленное количество звезд, большинство из которых настолько тусклые, что наблюдать невооруженным взглядом их невозможно. А само понятие звездной величины применяется не только для далеких звезд, но и для других объектов – Солнца, Луны, искусственных спутников, планет и так далее. Поэтому и считается, что звездная величина – это безразмерная числовая характеристика яркости объекта.
Как следует из вышесказанного, видимая звездная величина самых ярких объектов будет отрицательная. Для сравнения, звездная величина Солнца равна –26,7, а звездная величина ближайшей к нашему светилу, но не видимой невооруженным взглядом звезды Проксима Центавра составляет +11,1. Максимальная звездная величина Марса равна ? 2,91. Спутник «Маяк», который создали и планируют отправить на орбиту молодые российские ученые, как запланировано должен иметь звездную величину не более ?10. И если все удастся, он на некоторое время станет самым ярким объектом на ночном небе, если, конечно, не считать Луны в полнолуние (?12,74).
Основные формулы
Афелий орбиты рассчитывается по формуле raf=(1+e)a,{\displaystyle r_{\mathrm {af} }=(1+e)a,} где
-
- a — большая полуось;
- е — .
Линейная скорость планеты в афелии рассчитывается по формуле
- vaf=GM⊙(1−e)a(1+e),{\displaystyle v_{\mathrm {af} }={\sqrt {\frac {GM_{\odot }(1-e)}{a(1+e)}}},} где
-
- G — гравитационная постоянная;
- M⊙{\displaystyle M_{\odot }}— масса Солнца;
- a — большая полуось;
- е — .
Угловая скорость планеты в афелии относительно Солнца, выраженная в радианах в секунду, рассчитывается по формуле
- φ˙af=vafraf=GM⊙(1−e)a3(1+e)3.{\displaystyle {\dot {\varphi }}_{\mathrm {af} }={\frac {v_{\mathrm {af} }}{r_{\mathrm {af} }}}={\sqrt {\frac {GM_{\odot }(1-e)}{a^{3}(1+e)^{3}}}}.}
И линейная, и угловая скорость в афелии достигают своего минимума, тогда как в перигелии они максимальны.
Марс
Его орбита более округлая по сравнению с меркурианской. Но значимые изменения в периоды прохождения афелия и перигелия все же происходят. Они проявляются тем, что времена года на одном полушарии будут отличаться от другого по продолжительности и по температурам. Когда в северном полушарии начинается лето, планета находится на максимальном удалении, поэтому оно не такое теплое, но более продолжительное. В южном — наоборот, более короткое, но более теплое, потому что в этот период Марс проходит перигелий.
Что касается температур, то о них трудно говорить, потому что они резко меняются не только относительно зимы и лета, но и в течение суток, которые почти не отличаются от земных. Например, на экваторе днем планета может прогреться и до +28 градусов, однако уже ночью температура может упасть до -40 и ниже. Минимальная температура на полюсах близка к отметке -150 градусов.
Фактор, отвечающий за смену времен года
За сезонность на планетах Солнечной системы отвечает угол наклона оси вращения к орбите. Чем меньше угол, тем стабильнее погода на небесном теле и нет смены пор года. Также сезонности не бывает на небесных телах с углом наклона более 90°.
Смена сезонов характерна для объектов с углом наклона оси в пределах 20-30 градусов:
- Земля (23,3°);
- Марс (25,2°);
- Сатурн (29°);
- Нептун (30°).
«Лето» и «зима» также
есть на Меркурии, несмотря на практически отсутствующий наклон оси. Это связано
с высоким эксцентриситетом его орбиты. Разница между температурами в точках
перигелия и афелия на Меркурии составляет 620 градусов Цельсия.
Таким образом, величина и форма пути, который описывает объект вокруг Солнца, очень влияют на формирование температурных условий на нём. Именно невысокий эксцентриситет и небольшая удаленность движения Земли, а также оптимальный угол наклона оси сделали её температуру наиболее комфортной для существования живых организмов.
Терминология
Слова «перицентра» и «апоцентре» часто видел, хотя перицентр/апоцентр являются предпочтительными в технической эксплуатации.
- Для общих ситуаций, где основным является не указано, условия перицентре и апоцентре используются для обозначения крайних точек орбит (см. таблицу, верхний рисунок); перицентр и апоцентр (или apapsis) эквивалентных альтернатив, но эти термины также часто ссылаются на расстояния—то есть, наименьшее и наибольшее расстояния между орбитальным кораблем и его теле хозяина (см. Второй рисунок).
- На тело, вращающееся вокруг Солнца, точки наименьшего расстояния в перигелии (), и точка наибольшего расстояние представляет собой афелий (); при обсуждении орбитам вокруг других звезд термины становятся периастра и apastron.
- При обсуждении спутника Земли, включая Луну, точка наименьшего расстояния в перигее (), и наибольшее расстояние, на апогей (от греч. Γῆ (Gē), «земля» или «земля»).
- Нет естественных спутников Луны. Для техногенных объектов на лунной орбите, точки наименьшего расстояния можно назвать pericynthion () и максимальное расстояние apocynthion (); или perilune и apolune иногда используются.
Этимология
Слова перигелий и афелий был придуман Иоганном Кеплером для описания орбитального движения планет вокруг Солнца.
Слова образуются из префикса Пери- (греч. περί, рядом) и АПО- (греч. ἀπό, от), прикрепленному к греческого слова Солнце (ἥλιοςили hēlíou).
Различные термины используются для других небесных объектов. Суффиксы -гы, -Гелион, -Астрон и -galacticon часто используются в астрономической литературе, когда речь идет о Земле, Солнце, звезды, центр галактики соответственно. Суффикс -Юпитер иногда используется для Юпитера, но -saturnium очень редко использовался в последние 50 лет для Сатурна. Интернет -гы форма также используется как родовое ближайший подход-на «планета» термин—вместо того, чтобы применять его только на Землю.
Во время Аполлона программы, сроки pericynthion и apocynthion были использованы при обращении к орбите Луны; они ссылаются Синтия, альтернативное название для греческая богиня Луны Артемида. Что касается черных дыр, условия perimelasma и apomelasma (от греческого корня) были использованы физик и писатель-фантаст Джеффри А. Лэндис в 1998 история, которая произошла перед perinigricon и aponigricon (от лат.) появился в научной литературе в 2002 году, а до peribothron (от греч bothros, что означает отверстие или яму) в 2015 году.
Терминология резюме
Суффиксы показано ниже, могут быть добавлены префиксы Пери- и АПО- в виде уникальных имен апсид для орбитальных органов указанного узла/(первичной) системы. Однако, только за землю и системы Солнце-это уникальные суффиксы обычно используется. Как правило, для других хост-систем универсальный суффикс, -апсидой, используется вместо..
| Астрономический объект размещения | Солнце | Ртуть | Венера | Земля | Луна | Марс | Церера | Юпитер | Сатурн |
|---|---|---|---|---|---|---|---|---|---|
| Суффикс | ‑Гелион | ‑hermion | ‑cythe | ‑гы | ‑луна ‑cynthion‑selene | ‑areion | ‑Деметра | ‑Юпитер | ‑хрона ‑Кронос ‑saturnium‑крона |
| Происхожденияназвание | Гелиос | Гермес | Cytherean | Гайя | ЛунаСинтияСелена | Арес | Деметра | ЗевсЮпитер | КроносСатурн |
| Астрономические хозяина объект | Звезда | Галактика | Барицентр | Черная дыра |
|---|---|---|---|---|
| Суффикс | ‑Астрон | ‑galacticon | ‑центр‑фокус‑апсис | ‑мелазма‑bothron‑nigricon |
| Происхожденияназвание | Широта: Астра; звезды |
Гр: галаксии; галактики |
Gr: мелос; черныйGr: bothros; holeLat: niger; черный |
Афелий
В этой точке окружности космический объект максимально отдаляется от Солнца. Не имеет значения для всех тех планет, о которых говорилось в предыдущем разделе. Стоит отметить, что на самом деле название «афелий» появилось позднее. Изначально данная точка называлась «апогелий». Просто когда-то давно в записях кто-то решил разделить слово на две части, сократив его: ap.helios. При прочтении точка между частями слова не была замечена, и кто-то прочитал сочетание букв ph как «ф», как оно читается в английском языке. С тех пор название «афелий» вошло и закрепилось в различных языках. Земля каждый год проходит эту точку 4-5 июля.
Эти орбитальные центры являются важными точками не только для астрономов, перигелии и афелии в астрологии тоже занимают не последнее место. Они используются для составления прогнозов и предсказаний глобальных событий.
Решение в рамках общей теории относительности
Альберт Эйнштейн, 1921
Основная статья: Задача Кеплера в общей теории относительности
После создания в 1905 году специальной теории относительности (СТО) А. Эйнштейн осознал необходимость разработки релятивистского варианта теории тяготения, поскольку уравнения Ньютона были несовместимы с преобразованиями Лоренца, а скорость распространения ньютоновской гравитации была бесконечна. В одном из писем 1907 года Эйнштейн сообщал:
Первые наброски релятивистской теории тяготения опубликовали в начале 1910-х годов Макс Абрахам, Гуннар Нордстрём и сам Эйнштейн. У Абрахама смещение перигелия Меркурия было втрое меньше реального, в теории Нордстрёма ошибочным было даже направление смещения, версия Эйнштейна 1912 года давала значение на треть меньше наблюдаемого.
В 1913 году Эйнштейн сделал решающий шаг — перешёл от скалярного гравитационного потенциала к тензорному представлению, этот аппарат позволил адекватно описать неевклидову метрику пространства-времени. В 1915 году Эйнштейн опубликовал окончательный вариант своей новой теории тяготения, получившей название «общая теория относительности» (ОТО). В ней, в отличие от ньютоновской модели, вблизи массивных тел геометрия пространства-времени заметно отличается от евклидовой, что приводит к отклонениям от классической траектории движения планет.
18 ноября 1915 года Эйнштейн рассчитал (приближённо) это отклонение и получил практически точное совпадение с наблюдаемыми 43″ в столетие. При этом не понадобилось никакой подгонки констант и не делалось никаких произвольных допущений. Если обозначить:
- M{\displaystyle M} — масса Солнца;
- c{\displaystyle c} — скорость света;
- A{\displaystyle A} — величина большой полуоси орбиты планеты;
- e{\displaystyle e} — эксцентриситет орбиты;
- T{\displaystyle T} — период обращения,
то дополнительное смещение перигелия планеты (в радианах за оборот) в ОТО даётся формулой:
| δφ ≈ 6πGMc2A(1−e2) = 24π3A2T2c2(1−e2){\displaystyle \delta \varphi \ \approx \ {\frac {6\,\pi \,G\,M}{c^{2}\,A\,\left(1-e^{2}\right)}}\ =\ {\frac {24\,\pi ^{3}\,A^{2}}{T^{2}\,c^{2}\,\left(1-e^{2}\right)}}} |
Для Меркурия эта формула даёт 42,98″ за столетие в отличном соответствии с наблюдениями. Точное решение уравнений Эйнштейна, полученное Карлом Шварцшильдом два месяца спустя (январь 1916, уже после открытия окончательной версии уравнений поля), подтвердило приведённую формулу.
До 1919 года, когда Артур Эддингтон обнаружил гравитационное отклонение света, объяснение смещения перигелия Меркурия было единственным экспериментальным подтверждением теории Эйнштейна. В 1916 году Гарольд Джеффрис выразил сомнение в адекватности ОТО, поскольку она не объясняла смещение узлов орбиты Венеры, ранее указанное Ньюкомом. В 1919 году Джеффрис снял свои возражения, поскольку, по новым данным, никаких аномалий в движении Венеры, которые не укладывались бы в теорию Эйнштейна, обнаружено не было.
Тем не менее критика ОТО продолжалась некоторое время и после 1919 года. Некоторые астрономы высказывали мнение, что совпадение теоретического и наблюдаемого смещения перигелия Меркурия может быть случайным, или оспаривали достоверность наблюдаемого значения 43″. Современные точные измерения подтвердили оценки смещения перигелия планет и астероидов, предложенные ОТО.
| Небесное тело | Теоретическоезначение | Наблюдаемоезначение |
|---|---|---|
| Меркурий | 00043,0 | 0043,1 ± 0,5 |
| Венера | 00008,6 | 0008,4 ± 4,8 |
| Земля | 00003,8 | 0005,0 ± 1,2 |
| Марс | 00001,35 | 0001,1 ± 0,3 |
| Икар (астероид) | 00010,1 | 0009,8 ± 0,8 |
Большая погрешность данных для Венеры и Земли вызвана тем, что их орбиты почти круговые.
Формула ОТО была проверена также для двойной звезды-пульсара PSR B1913+16, в которой две звезды, по массе сравнимые с Солнцем, вращаются на близком расстоянии, и поэтому релятивистское смещение периастра каждой (аналога перигелия) очень велико. Наблюдения показали смещение на 4,2 градуса в год, в полном согласии с ОТО. Самое большое смещение периастра обнаружено у открытого в 2003 году двойного пульсара PSR J0737−3039 — на 17 градусов в год; измерения 2005 года показали соответствие динамики системы предсказаниям ОТО с точностью 0,05 % в доверительном интервале 3σ{\displaystyle 3\sigma }.
В 2020 году завершились более чем 30-летние измерения релятивистского смещения периастра для движения звезды вокруг компактного радиоисточника Стрелец A* (предположительно чёрной дыры) в центре нашей Галактики. Измерения проводил немецкий Институт внеземной физики Макса Планка. Результаты полностью соответствовали предсказаниям ОТО.
Меркурий в 2019 году
Дата: 14.03.2019
15 марта 2019 года в 05:00 мск Меркурий пройдет нижнее соединение с Солнцем. В 2019 году первая планета трижды окажется в нижнем соединении: 15 марта, 21 июля и 11 ноября. 11 ноября 2019 года случится достаточно редкое астрономическое явление — прохождение Меркурия по диску Солнца.
Прохождение по солнечному диску может наступить только в нижнем соединении около одного из узлов орбиты Меркурия — в мае или ноябре. Из-за вытянутости орбиты Меркурия майские прохождения случаются особенно редко, через 13 или 33 года после предыдущего явления. В XXI веке майские прохождения уже произошли в 2003 и 2016 г., оба были хорошо видны в России, а следующее будет только в 2049 г. Ноябрьские прохождения происходят с интервалом в 13 лет, а иногда — 7 лет. В XXI веке ноябрьское прохождение Меркурия было в 2006 году, а следующее после 11 ноября 2019 года случится в 2032 году. Это редкое астрономическое явление 11 ноября 2019 года в России будет видно только в западных и центральных районах нашей страны в своей начальной фазе. Полностью все явление можно будет наблюдать в западном полушарии.
Видео: Прохождение Меркурия по диску Солнца 9 мая 2016 года.
Наблюдать Меркурий можно было в конце февраля начале марта 2019 года по вечерам сразу после захода Солнца, сейчас он скрывается в солнечных лучах и с Земли не виден. В момент нижнего соединения с Солнцем Меркурий движется по созвездию Рыбы.

Наилучшая видимость первой от Солнца планеты — вечерняя или утренняя — наступает в моменты, когда с позиции земного наблюдателя её удаление от Солнца максимально, т.е. Меркурий находится в наибольшей восточной или западной элонгации.
*Элонгация – от позднелатинского слова elongatio – удаление – геоцентрический угол между планетой и Солнцем.
Для Меркурия максимальное возможное значение элонгации — 28°. Из-за того, что орбита Меркурия не вполне круговая, угловое расстояние от Солнца в момент элонгации может быть разным — от 18° до 28°.
Такую точку (астрономы называют ее максимальной восточной элонгацией) Меркурий прошел – 27 февраля 2019 года достигнув углового удаления от Солнца – 18°! Следующий раз точку восточной элонгации в 2019 году Меркурий пройдет 24 июня (25°) и 20 октября (25°).
Западная элонгация Меркурия в 2019 году произойдет 11 апреля, 10 августа и 28 ноября. 11 апреля планета удалится от Солнца на 28°– достигнув максимального углового удаления от Солнца в 2019 году! Точку верхнего соединения с Солнцем в 2019 году Меркурий пройдет 21 мая и 4 сентября. В нижнем соединении с Солнцем в 2019 году Меркурий окажется 21 июля и 11 ноября. Кстати, 11 ноября 2019 года произойдет особенное событие года – Меркурий пройдет по диску Солнца.
2019-й год подарит три периода видимости Меркурия: вечерняя – в феврале-марте и две утренние: в августе и ноябре-декабре. Осенью будет самая благоприятная утренняя видимость Меркурия в 2019 году. К концу ноября месяца продолжительность видимости планеты увеличится до 1,3 часов. Для наблюдения Меркурия в периоды видимости нужен бинокль, открытый горизонт и ясное небо.
В марте 2019 года Меркурий движется по созвездиям Рыбы и Водолей. Видимая звёздная величина Меркурия уменьшается от 1,1 до 0,1, и его нелегко заметить из-за близости к Солнцу.

Меркурий — самая маленькая и самая близкая к Солнцу планета Солнечной системы. Среднее расстояние Меркурия от Солнца 58 млн км. Меркурий очень быстро обращается вокруг Солнца, делая один круг за 88 земных суток. Планета названа в честь древнеримского бога торговли. Меркурий относится к планетам земной группы. У него нет естественных спутников, но есть очень разреженная атмосфера. Его диаметр всего 4879 км. Планета обладает крупным железным ядром, которое составляет 83 % от всего объёма планеты. Близость к Солнцу и довольно медленное вращение планеты вокруг своей оси, а также крайне разреженная атмосфера приводят к тому, что на Меркурии наблюдаются самые резкие перепады температур в Солнечной системе. Температура на поверхности Меркурия колеблется от −180°C до +430 °C. Солнечная сторона нагревается гораздо больше, чем полярные области и обратная сторона планеты. Этому способствует также рыхлая поверхность Меркурия, которая плохо проводит тепло. По своим физическим характеристикам и внешнему виду Меркурий напоминает Луну.
Параллакс
Никогда не задумывались, как ученые определяют расстояние до звезды? Ведь лазерным дальномером это расстояние не измеришь. На самом деле, все просто. В течение года положение звезды на небе изменяется вследствие обращения Земли по орбите вокруг Солнца. Такое изменение называется годичным параллаксом звезды. Чем ближе звезда к нам, тем больше ее смещение на фоне звезд, которые находятся дальше. Но даже у ближайших звезд такое смещение чрезвычайно мало. Невозможность обнаружить параллакс у звезд в свое время была одним из аргументов против гелиоцентрической системы мира. Удалось это сделать только в XIX веке. В нынешнее время для измерения параллаксов, а следовательно и расстояний до звезд, на орбиты выводят специальные космические телескопы. Телескоп Hipparcos Европейского космического агентства (названный в честь того самого Гиппарха, который классифицировал звезды по яркости) позволил измерить параллаксы более 100 тысяч звезд. В декабре 2013 года выведен на орбиту его преемник Gaia.

Параллактическое смещение близких звезд на фоне далёких / wikimedia.org
Собственно, параллакс (а это не только астрономическое понятие) представляет собой изменение видимого положения объекта относительно удаленного фона (в нашем случае более дальних звезд) в зависимости от положения наблюдателя. Используется он и в геодезии. Имеет значение для фотографии. Измеряется параллакс в угловых секундах (секундах дуги).